The MI Procedure

Monotone and FCS Logistic Regression Methods

Subsections:

The logistic regression method is another imputation method available for classification variables. In the logistic regression method, a logistic regression model is fitted for a classification variable with a set of covariates constructed from the effects, where the classification variable is an ordinal response or a nominal response variable.

In the MI procedure, ordered values are assigned to response levels in ascending sorted order. If the response variable Y takes values in $\{ 1,\ldots ,K\} $, then for ordinal response models, the cumulative model has the form

\[ \mbox{logit}(\Pr (Y\le j | \mb{x})) = \mbox{log} \left(\frac{\Pr (Y\le j | \mb{x})}{1-\Pr (Y\le j | \mb{x})} \right) = \alpha _{j} + \bbeta ’ \mb{x} , \quad j=1,\ldots ,K-1 \]

where $\alpha _{1},\ldots ,\alpha _{K-1}$ are K-1 intercept parameters, and $\bbeta $ is the vector of slope parameters.

For nominal response logistic models, where the K possible responses have no natural ordering, the generalized logit model has the form

\[ \log \left(\frac{\Pr ({Y} = j~ |~ \mb{x})}{\Pr ({Y} = K~ |~ \mb{x})}\right)= \alpha _{j} + \bbeta _{j} ’ \mb{x} , \quad j=1,\ldots ,K-1 \]

where the $\alpha _{1},\ldots ,\alpha _{K-1}$ are K-1 intercept parameters, and the $\bbeta _{1},\ldots ,\bbeta _{K-1}$ are K-1 vectors of slope parameters.

Binary Response Logistic Regression

For a binary classification variable, based on the fitted regression model, a new logistic regression model is simulated from the posterior predictive distribution of the parameters and is used to impute the missing values for each variable (Rubin, 1987, pp. 167–170).

For a binary variable Y with responses 1 and 2, a logistic regression model is fitted using observations with observed values for the imputed variable Y:

\[ \mr{logit} (p_1) = {\beta }_{0} + {\beta }_{1} \, X_{1} + {\beta }_{2} \, X_{2} + \ldots + {\beta }_{p} \, X_{p} \]

where $X_{1}, X_{2}, \ldots , X_{p}$ are covariates for Y,   $p_1 = \mr{Pr}( Y=1 | X_{1}, X_{2}, \ldots , X_{p} )$,   and   $\mr{logit} (p_1) = \mr{log} ( p_1 / (1-p_1) )$

The fitted model includes the regression parameter estimates $\hat{\bbeta } = (\hat{\beta }_{0}, \hat{\beta }_{1}, \ldots , \hat{\beta }_{p})$ and the associated covariance matrix $\mb{V}$.

The following steps are used to generate imputed values for a binary variable Y with responses 1 and 2:

  1. New parameters 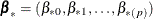$\bbeta _{*} = ({\beta }_{*0}, {\beta }_{*1}, \ldots , {\beta }_{*(p)})$ are drawn from the posterior predictive distribution of the parameters.

    \[ \bbeta _{*} = \hat{\bbeta } + \mb{V}_{h}’ \mb{Z} \]

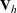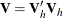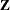    where $\mb{V}_{h}$ is the upper triangular matrix in the Cholesky decomposition, $\mb{V} = \mb{V}_{h}’ \mb{V}_{h}$, and $\mb{Z}$ is a vector of 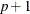$p+1$ independent random normal variates.

  2. For an observation with missing 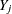$Y_{j}$ and covariates 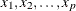$x_{1}, x_{2}, \ldots , x_{p}$, compute the predicted probability that Y= 1:

    \[ p_1 = \frac{\mr{exp}({\mu }_1)}{1+\mr{exp}({\mu }_1)} \]

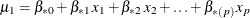    where ${\mu }_1 = {\beta }_{*0} + {\beta }_{*1} \, x_{1} + {\beta }_{*2} \, x_{2} + \ldots + {\beta }_{*(p)} \, x_{p}$.

  3. Draw a random uniform variate, u, between 0 and 1. If the value of u is less than 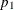$p_1$, impute Y= 1; otherwise impute Y= 2.

The binary logistic regression imputation method can be extended to include the ordinal classification variables with more than two levels of responses, and the nominal classification variables. The LINK=LOGIT and LINK=GLOGIT options can be used to specify the cumulative logit model and the generalized logit model, respectively. The options ORDER= and DESCENDING can be used to specify the sort order for the levels of the imputed variables.

Ordinal Response Logistic Regression

For an ordinal classification variable, based on the fitted regression model, a new logistic regression model is simulated from the posterior predictive distribution of the parameters and is used to impute the missing values for each variable.

For a variable Y with ordinal responses 1, 2, …, K, a logistic regression model is fitted using observations with observed values for the imputed variable Y:

\[ \mr{logit} (p_{j}) = {\alpha }_{j} + {\beta }_{1} \, X_{1} + {\beta }_{2} \, X_{2} + \ldots + {\beta }_{p} \, X_{p} \]

where $X_{1}, X_{2}, \ldots , X_{p}$ are covariates for Y and   $p_{j} = \mr{Pr}( Y \leq j | X_{1}, X_{2}, \ldots , X_{k} )$.

The fitted model includes the regression parameter estimates $\hat{\alpha }= (\hat{\alpha }_{0}, \ldots , \hat{\alpha }_{K-1})$ and $\hat{\bbeta }= (\hat{\beta }_{0}, \hat{\beta }_{1}, \ldots , \hat{\beta }_{k})$, and their associated covariance matrix $\mb{V}$.

The following steps are used to generate imputed values for an ordinal classification variable Y with responses 1, 2, …, K:

  1. New parameters 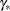$\gamma _{*}$ are drawn from the posterior predictive distribution of the parameters.

    \[ \gamma _{*} = \hat{\gamma } + \mb{V}_{h}’ \mb{Z} \]

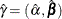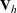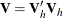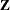    where $\hat{\gamma }= (\hat{\alpha }, \hat{\bbeta })$, $\mb{V}_{h}$ is the upper triangular matrix in the Cholesky decomposition, $\mb{V} = \mb{V}_{h}’ \mb{V}_{h}$, and $\mb{Z}$ is a vector of 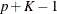$p+K-1$ independent random normal variates.

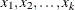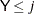  2. For an observation with missing Y and covariates $x_{1}, x_{2}, \ldots , x_{k}$, compute the predicted cumulative probability for $\Variable{Y} \leq j$:

    \[ p_ j= \mr{pr}(\Variable{Y} \leq j) = \frac{ e^{\alpha _ j + \mb{x} ' \bbeta } }{ e^{\alpha _ j + \mb{x} ' \bbeta } + 1} \]

  3. Draw a random uniform variate, u, between 0 and 1, then impute

    \[ Y = \left\{ \begin{array}{ll} 1 & \mr{if} \; \Mathtext{u} < p_{1} \\ k & \mr{if} \; p_{k-1} \leq \Mathtext{u} < p_{k} \\ K & \mr{if} \; p_{K-1} \leq \Mathtext{u} \end{array} \right. \]

Nominal Response Logistic Regression

For a nominal classification variable, based on the fitted regression model, a new logistic regression model is simulated from the posterior predictive distribution of the parameters and is used to impute the missing values for each variable.

For a variable Y with nominal responses 1, 2, …, K, a logistic regression model is fitted using observations with observed values for the imputed variable Y:

\[ \mr{log} \left( \frac{p_{j}}{p_{K}} \right) = {\alpha }_{j} + {\beta }_{j1} \, X_{1} + {\beta }_{j2} \, X_{2} + \ldots + {\beta }_{jp} \, X_{p} \]

where $X_{1}, X_{2}, \ldots , X_{p}$ are covariates for Y and   $p_{j} = \mr{Pr}( Y = j | X_{1}, X_{2}, \ldots , X_{p} )$.

The fitted model includes the regression parameter estimates $\hat{\alpha }= (\hat{\alpha }_{0}, \ldots , \hat{\alpha }_{K-1})$ and $\hat{\bbeta }= (\hat{\bbeta }_{0}, \ldots , \hat{\beta }_{K-1})$, and their associated covariance matrix $\mb{V}$, where $\hat{\bbeta }_{j} = (\hat{\beta }_{j0}, \hat{\beta }_{j1}, \ldots , \hat{\beta }_{jp})$,

The following steps are used to generate imputed values for a nominal classification variable Y with responses 1, 2, …, K:

  1. New parameters 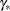$\gamma _{*}$ are drawn from the posterior predictive distribution of the parameters.

    \[ \gamma _{*} = \hat{\gamma } + \mb{V}_{h}’ \mb{Z} \]

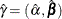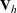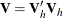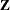    where $\hat{\gamma }= (\hat{\alpha }, \hat{\bbeta })$, $\mb{V}_{h}$ is the upper triangular matrix in the Cholesky decomposition, $\mb{V} = \mb{V}_{h}’ \mb{V}_{h}$, and $\mb{Z}$ is a vector of 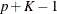$p+K-1$ independent random normal variates.

  2. For an observation with missing Y and covariates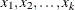 $x_{1}, x_{2}, \ldots , x_{k}$, compute the predicted probability for Y= j, j=1, 2, …, K-1:

    \[ \mr{pr}(\Variable{Y}=j) = \frac{ e^{ \alpha _ j + \mb{x} ' \bbeta _ j } }{ \sum _{k=1}^{K-1} {e^{ \alpha _ k + \mb{x} ' \bbeta _ k }} + 1 } \]

    and

    \[ \mr{pr}(\Variable{Y}=K) = \frac{ 1 }{ \sum _{k=1}^{K-1} {e^{ \alpha _ k + \mb{x} ' \bbeta _ k }} + 1 } \]

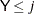  3. Compute the cumulative probability for $\Variable{Y} \leq j$:

    \[ P_ j= \sum _{k=1}^{j} \mr{pr}(\Variable{Y}=k) \]

  4. Draw a random uniform variate, u, between 0 and 1, then impute

    \[ Y = \left\{ \begin{array}{ll} 1 & \mr{if} \; \Mathtext{u} < p_{1} \\ k & \mr{if} \; p_{k-1} \leq \Mathtext{u} < p_{k} \\ K & \mr{if} \; p_{K-1} \leq \Mathtext{u} \end{array} \right. \]