The SURVEYFREQ Procedure
The following example shows how you can use PROC SURVEYFREQ to analyze sample survey data. The example uses data from a customer satisfaction survey for a student information system (SIS), which is a software product that provides modules for student registration, class scheduling, attendance, grade reporting, and other functions.
The software company conducted a survey of school personnel who use the SIS. A probability sample of SIS users was selected from the study population, which included SIS users at middle schools and high schools in the three-state area of Georgia, South Carolina, and North Carolina. The sample design for this survey was a two-stage stratified design. A first-stage sample of schools was selected from the list of schools in the three-state area that use the SIS. The list of schools (the first-stage sampling frame) was stratified by state and by customer status (whether the school was a new user of the system or a renewal user). Within the first-stage strata, schools were selected with probability proportional to size and with replacement, where the size measure was school enrollment. From each sample school, five staff members were randomly selected to complete the SIS satisfaction questionnaire. These staff members included three teachers and two administrators or guidance department members.
The SAS data set SIS_Survey contains the survey results, as well as the sample design information needed to analyze the data. This data set includes
an observation for each school staff member responding to the survey. The variable Response contains the staff member’s response about overall satisfaction with the system.
The variable State contains the school’s state, and the variable NewUser contains the school’s customer status ('New Customer' or 'Renewal Customer'). These two variables determine the first-stage
strata from which schools were selected. The variable School contains the school identification code and identifies the first-stage sampling units (clusters). The variable SamplingWeight contains the overall sampling weight for each respondent. Overall sampling weights were computed from the selection probabilities
at each stage of sampling and were adjusted for nonresponse.
Other variables in the data set SIS_Survey include SchoolType and Department. The variable SchoolType identifies the school as a high school or a middle school. The variable Department identifies the staff member as a teacher, or an administrator or guidance department member.
The following PROC SURVEYFREQ statements request a one-way frequency table for the variable Response:
title 'Student Information System Survey'; proc surveyfreq data=SIS_Survey; tables Response; strata State NewUser; cluster School; weight SamplingWeight; run;
The PROC SURVEYFREQ statement invokes the procedure and identifies the input data set to be analyzed. The TABLES statement
requests a one-way frequency table for the variable Response. The table request syntax for PROC SURVEYFREQ is very similar to the table request syntax for PROC FREQ. This example shows
a request for a single one-way table, but you can also request two-way tables and multiway tables. As in PROC FREQ, you can
request more than one table in the same TABLES statement, and you can use multiple TABLES statements in the same invocation
of the procedure.
The STRATA, CLUSTER, and WEIGHT statements provide sample design information for the procedure, so that the analysis is done
according to the sample design used for the survey, and the estimates apply to the study population. The STRATA statement
names the variables State and NewUser, which identify the first-stage strata. Note that the design for this example also includes stratification at the second
stage of selection (by type of school personnel), but you specify only the first-stage strata for PROC SURVEYFREQ. The CLUSTER
statement names the variable School, which identifies the clusters (primary sampling units). The WEIGHT statement names the sampling weight variable.
Figure 90.1 and Figure 90.2 display the output produced by PROC SURVEYFREQ, which includes the “Data Summary” table and the one-way table, “Table of Response.” The “Data Summary” table is produced by default unless you specify the NOSUMMARY option. This table shows there are 6 strata, 370 clusters or
schools, and 1850 observations (respondents) in the SIS_Survey data set. The sum of the sampling weights is approximately 39,000, which estimates the total number of school personnel in
the study area that use the SIS.
Figure 90.1: SIS_Survey Data Summary
| Student Information System Survey |
| Data Summary | |
|---|---|
| Number of Strata | 6 |
| Number of Clusters | 370 |
| Number of Observations | 1850 |
| Sum of Weights | 38899.6482 |
Figure 90.2 displays the one-way table of Response, which provides estimates of the population total (weighted frequency) and the population percentage for each category (level)
of the variable Response. The response level 'Very Unsatisfied' has a frequency of 304, which means that 304 sample respondents fall into this category.
It is estimated that 17.17% of all school personnel in the study population fall into this category, and the standard error
of this estimate is 1.29%. Note that the estimates apply to the population of all SIS users in the study area, as opposed
to describing only the sample of 1850 respondents. The estimate of the total number of school personnel that are 'Very Unsatisfied'
is 6,678, with a standard deviation of 502. The standard errors computed by PROC SURVEYFREQ are based on the multistage stratified
design of the survey. This differs from some of the traditional analysis procedures, which assume the design is simple random
sampling from an infinite population.
Figure 90.2: One-Way Table of Response
| Table of Response | |||||
|---|---|---|---|---|---|
| Response | Frequency | Weighted Frequency |
Std Dev of Wgt Freq |
Percent | Std Err of Percent |
| Very Unsatisfied | 304 | 6678 | 501.61039 | 17.1676 | 1.2872 |
| Unsatisfied | 326 | 6907 | 495.94101 | 17.7564 | 1.2712 |
| Neutral | 581 | 12291 | 617.20147 | 31.5965 | 1.5795 |
| Satisfied | 455 | 9309 | 572.27868 | 23.9311 | 1.4761 |
| Very Satisfied | 184 | 3714 | 370.66577 | 9.5483 | 0.9523 |
| Total | 1850 | 38900 | 129.85268 | 100.000 | |
The following PROC SURVEYFREQ statements request confidence limits for the percentages, a chi-square goodness-of-fit test,
and a weighted frequency plot for the one-way table of Response. The ODS GRAPHICS ON statement enables ODS Graphics.
title 'Student Information System Survey';
ods graphics on;
proc surveyfreq data=SIS_Survey nosummary;
tables Response / clwt nopct chisq
plots=WtFreqPlot;
strata State NewUser;
cluster School;
weight SamplingWeight;
run;
ods graphics off;
The NOSUMMARY option in the PROC SURVEYFREQ statement suppresses the “Data Summary” table. In the TABLES statement, the CLWT option requests confidence limits for the weighted frequencies (totals). The NOPCT option suppresses display of the weighted frequencies and their standard deviations. The CHISQ option requests a Rao-Scott chi-square goodness-of-fit test, and the PLOTS= option requests a weighted frequency plot. ODS Graphics must be enabled before producing plots.
Figure 90.3 shows the one-way table of Response, which includes confidence limits for the weighted frequencies. The 95% confidence limits for the total number of users that
are 'Very Unsatisfied' are 5692 and 7665. To change the ![]() level of the confidence limits, which equals 5% by default, you can use the ALPHA= option. Like the other estimates and standard
errors produced by PROC SURVEYFREQ, these confidence limit computations take into account the complex survey design and apply
to the entire study population.
level of the confidence limits, which equals 5% by default, you can use the ALPHA= option. Like the other estimates and standard
errors produced by PROC SURVEYFREQ, these confidence limit computations take into account the complex survey design and apply
to the entire study population.
Figure 90.3: Confidence Limits for Response Totals
| Student Information System Survey |
| Table of Response | |||||
|---|---|---|---|---|---|
| Response | Frequency | Weighted Frequency |
Std Dev of Wgt Freq |
95% Confidence Limits for Wgt Freq |
|
| Very Unsatisfied | 304 | 6678 | 501.61039 | 5692 | 7665 |
| Unsatisfied | 326 | 6907 | 495.94101 | 5932 | 7882 |
| Neutral | 581 | 12291 | 617.20147 | 11077 | 13505 |
| Satisfied | 455 | 9309 | 572.27868 | 8184 | 10435 |
| Very Satisfied | 184 | 3714 | 370.66577 | 2985 | 4443 |
| Total | 1850 | 38900 | 129.85268 | 38644 | 39155 |
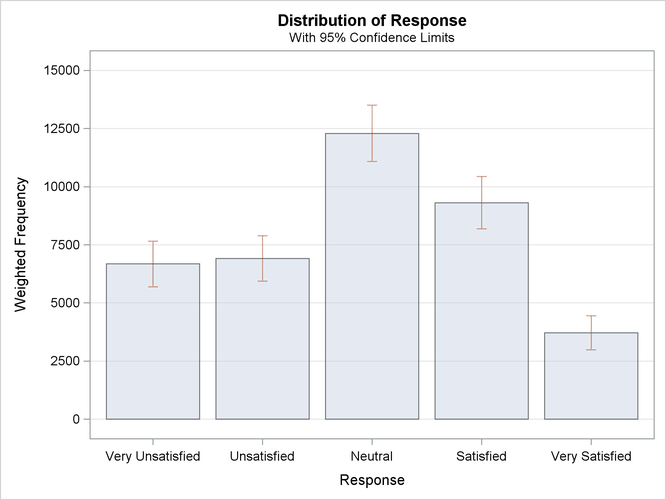
Figure 90.4 displays the weighted frequency plot of Response. The plot displays weighted frequencies (totals) together with their confidence limits in the form of a vertical bar chart.
You can use the PLOTS= option to request a dot plot instead of a bar chart or to plot percentages instead of weighted frequencies.
Figure 90.5 shows the chi-square goodness-of-fit results for the table of Response. The null hypothesis for this test is equal proportions for the levels of the one-way table. (To test a null hypothesis of
specified proportions instead of equal proportions, you can use the TESTP= option to specify null hypothesis proportions.)
The chi-square test provided by the CHISQ option is the Rao-Scott design-adjusted chi-square test, which takes the sample
design into account and provides inferences for the study population. To produce the Rao-Scott chi-square statistic, PROC
SURVEYFREQ first computes the usual Pearson chi-square statistic based on the weighted frequencies, and then adjusts this
value with a design correction. An F approximation is also provided. For the table of Response, the F value is 30.0972 with a p-value of <0.0001, which indicates rejection of the null hypothesis of equal proportions for all response levels.
Figure 90.5: Chi-Square Goodness-of-Fit Test for Response
| Rao-Scott Chi-Square Test | |
|---|---|
| Pearson Chi-Square | 251.8105 |
| Design Correction | 2.0916 |
| Rao-Scott Chi-Square | 120.3889 |
| DF | 4 |
| Pr > ChiSq | <.0001 |
| F Value | 30.0972 |
| Num DF | 4 |
| Den DF | 1456 |
| Pr > F | <.0001 |
| Sample Size = 1850 | |
Continuing to analyze the SIS_Survey data, the following PROC SURVEYFREQ statements request a two-way table of SchoolType by Response:
title 'Student Information System Survey';
ods graphics on;
proc surveyfreq data=SIS_Survey nosummary;
tables SchoolType * Response /
plots=wtfreqplot(type=dot scale=percent groupby=row);
strata State NewUser;
cluster School;
weight SamplingWeight;
run;
ods graphics off;
The STRATA, CLUSTER, and WEIGHT statements do not change from the one-way table analysis, because the sample design and the input data set are the same. These SURVEYFREQ statements request a different table but specify the same sample design information.
The ODS GRAPHICS ON statement enables ODS Graphics. The PLOTS= option in the TABLES statement requests a plot of SchoolType by Response, and the TYPE=DOT plot-option specifies a dot plot instead of the default bar chart. The SCALE=PERCENT plot-option requests a plot of percentages instead of totals. The GROUPBY=ROW plot-option groups the graph cells by the row variable (SchoolType).
Figure 90.6 shows the two-way table produced for SchoolType by Response. The first variable named in the two-way table request, SchoolType, is referred to as the row variable, and the second variable, Response, is referred to as the column variable. Two-way tables display all column variable levels for each row variable level. This two-way table lists all levels of the
column variable Response for each level of the row variable SchoolType, 'Middle School' and 'High School'. Also SchoolType = 'Total' shows the distribution of Response overall for both types of schools. And Response = 'Total' provides totals over all levels of response, for each type of school and overall. To suppress these totals, you
can specify the NOTOTAL option.
Figure 90.6: Two-Way Table of SchoolType by Response
| Student Information System Survey |
| Table of SchoolType by Response | ||||||
|---|---|---|---|---|---|---|
| SchoolType | Response | Frequency | Weighted Frequency |
Std Dev of Wgt Freq |
Percent | Std Err of Percent |
| Middle School | Very Unsatisfied | 116 | 2496 | 351.43834 | 6.4155 | 0.9030 |
| Unsatisfied | 109 | 2389 | 321.97957 | 6.1427 | 0.8283 | |
| Neutral | 234 | 4856 | 504.20553 | 12.4847 | 1.2953 | |
| Satisfied | 197 | 4064 | 443.71188 | 10.4467 | 1.1417 | |
| Very Satisfied | 94 | 1952 | 302.17144 | 5.0193 | 0.7758 | |
| Total | 750 | 15758 | 1000 | 40.5089 | 2.5691 | |
| High School | Very Unsatisfied | 188 | 4183 | 431.30589 | 10.7521 | 1.1076 |
| Unsatisfied | 217 | 4518 | 446.31768 | 11.6137 | 1.1439 | |
| Neutral | 347 | 7434 | 574.17175 | 19.1119 | 1.4726 | |
| Satisfied | 258 | 5245 | 498.03221 | 13.4845 | 1.2823 | |
| Very Satisfied | 90 | 1762 | 255.67158 | 4.5290 | 0.6579 | |
| Total | 1100 | 23142 | 1003 | 59.4911 | 2.5691 | |
| Total | Very Unsatisfied | 304 | 6678 | 501.61039 | 17.1676 | 1.2872 |
| Unsatisfied | 326 | 6907 | 495.94101 | 17.7564 | 1.2712 | |
| Neutral | 581 | 12291 | 617.20147 | 31.5965 | 1.5795 | |
| Satisfied | 455 | 9309 | 572.27868 | 23.9311 | 1.4761 | |
| Very Satisfied | 184 | 3714 | 370.66577 | 9.5483 | 0.9523 | |
| Total | 1850 | 38900 | 129.85268 | 100.000 | ||
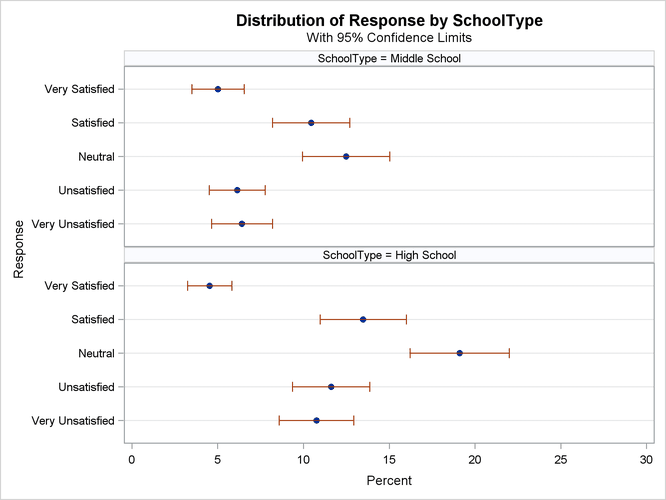
Figure 90.7 displays the weighted frequency dot plot that PROC SURVEYFREQ produces for the table of SchoolType and Response. The GROUPBY=ROW plot-option groups the graph cells by the row variable (SchoolType). If you do not specify GROUPBY=ROW, the procedure groups the graph cells by the column variable by default. You can plot
percentages instead of weighted frequencies by specifying the SCALE=PERCENT plot-option. You can use other plot-options to change the orientation of the plot or to request a different two-way layout.
By default, without any other TABLES statement options, a two-way table displays the frequency, the weighted frequency and its standard deviation, and the percentage and its standard error for each table cell (combination of row and column variable levels). But there are several options available to customize your table display by adding more information or by suppressing some of the default information.
The following PROC SURVEYFREQ statements request a two-way table of SchoolType by Response that displays row percentages, and also request a chi-square test of association between the two variables:
title 'Student Information System Survey'; proc surveyfreq data=SIS_Survey nosummary; tables SchoolType * Response / row nowt chisq; strata State NewUser; cluster School; weight SamplingWeight; run;
The ROW option in the TABLES statement requests row percentages, which give the distribution of Response within each level of the row variable SchoolType. The NOWT option suppresses display of the weighted frequencies and their standard deviations. The CHISQ option requests
a Rao-Scott chi-square test of association between SchoolType and Response.
Figure 90.8 displays the two-way table of SchoolType by Response. For middle schools, it is estimated that 25.79% of school personnel are satisfied with the student information system and
12.39% are very satisfied. For high schools, these estimates are 22.67% and 7.61%, respectively.
Figure 90.9 displays the chi-square test results. The Rao-Scott chi-square statistic equals 9.04, and the corresponding F value is 2.26 with a p-value of 0.0605. This indicates an association between school type (middle school or high school) and satisfaction with the student information system at the 10% significance level.
Figure 90.8: Two-Way Table with Row Percentages
| Student Information System Survey |
| Table of SchoolType by Response | ||||||
|---|---|---|---|---|---|---|
| SchoolType | Response | Frequency | Percent | Std Err of Percent |
Row Percent |
Std Err of Row Percent |
| Middle School | Very Unsatisfied | 116 | 6.4155 | 0.9030 | 15.8373 | 1.9920 |
| Unsatisfied | 109 | 6.1427 | 0.8283 | 15.1638 | 1.8140 | |
| Neutral | 234 | 12.4847 | 1.2953 | 30.8196 | 2.5173 | |
| Satisfied | 197 | 10.4467 | 1.1417 | 25.7886 | 2.2947 | |
| Very Satisfied | 94 | 5.0193 | 0.7758 | 12.3907 | 1.7449 | |
| Total | 750 | 40.5089 | 2.5691 | 100.000 | ||
| High School | Very Unsatisfied | 188 | 10.7521 | 1.1076 | 18.0735 | 1.6881 |
| Unsatisfied | 217 | 11.6137 | 1.1439 | 19.5218 | 1.7280 | |
| Neutral | 347 | 19.1119 | 1.4726 | 32.1255 | 2.0490 | |
| Satisfied | 258 | 13.4845 | 1.2823 | 22.6663 | 1.9240 | |
| Very Satisfied | 90 | 4.5290 | 0.6579 | 7.6128 | 1.0557 | |
| Total | 1100 | 59.4911 | 2.5691 | 100.000 | ||
| Total | Very Unsatisfied | 304 | 17.1676 | 1.2872 | ||
| Unsatisfied | 326 | 17.7564 | 1.2712 | |||
| Neutral | 581 | 31.5965 | 1.5795 | |||
| Satisfied | 455 | 23.9311 | 1.4761 | |||
| Very Satisfied | 184 | 9.5483 | 0.9523 | |||
| Total | 1850 | 100.000 | ||||
Figure 90.9: Chi-Square Test of No Association
| Rao-Scott Chi-Square Test | |
|---|---|
| Pearson Chi-Square | 18.7829 |
| Design Correction | 2.0766 |
| Rao-Scott Chi-Square | 9.0450 |
| DF | 4 |
| Pr > ChiSq | 0.0600 |
| F Value | 2.2613 |
| Num DF | 4 |
| Den DF | 1456 |
| Pr > F | 0.0605 |
| Sample Size = 1850 | |