The NLMIXED Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names
Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names -
Examples

- References
The FD= and FDHESSIAN= options specify the use of finite-difference approximations of the derivatives. The FD= option specifies that all derivatives are approximated using function evaluations, and the FDHESSIAN= option specifies that second-order derivatives are approximated using gradient evaluations.
Computing derivatives by finite-difference approximations can be very time-consuming, especially for second-order derivatives
based only on values of the objective function (FD= option). If analytical derivatives are difficult to obtain (for example, if a function is computed by an iterative process),
you might consider one of the optimization techniques that use first-order derivatives only (QUANEW, DBLDOG, or CONGRA). In
the expressions that follow, ![]() denotes the parameter vector,
denotes the parameter vector, ![]() denotes the step size for the ith parameter, and
denotes the step size for the ith parameter, and ![]() is a vector of zeros with a 1 in the ith position.
is a vector of zeros with a 1 in the ith position.
The forward-difference derivative approximations consume less computer time, but they are usually not as precise as approximations that use central-difference formulas.
-
For first-order derivatives, n additional function calls are required:
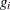
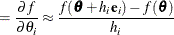
-
For second-order derivatives based on function calls only (Dennis and Schnabel, 1983, p. 80),
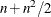 additional function calls are required for dense Hessian:
additional function calls are required for dense Hessian:
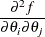
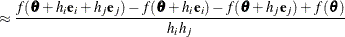
-
For second-order derivatives based on gradient calls (Dennis and Schnabel, 1983, p. 103), n additional gradient calls are required:
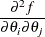
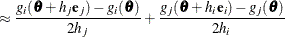
Central-difference approximations are usually more precise, but they consume more computer time than approximations that use forward-difference derivative formulas.
-
For first-order derivatives, 2n additional function calls are required:
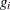
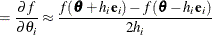
-
For second-order derivatives based on function calls only (Abramowitz and Stegun, 1972, p. 884),
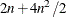 additional function calls are required.
additional function calls are required.
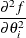
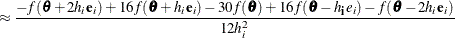
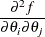
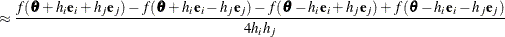
-
For second-order derivatives based on gradient calls, 2n additional gradient calls are required:
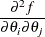
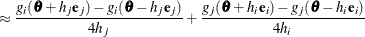
You can use the FDIGITS= option to specify the number of accurate digits in the evaluation of the objective function. This specification is helpful in determining an appropriate interval size h to be used in the finite-difference formulas.
The step sizes ![]() ,
, ![]() are defined as follows:
are defined as follows:
-
For the forward-difference approximation of first-order derivatives that use function calls and second-order derivatives that use gradient calls,
![$h_ j = \sqrt [2]{\eta } (1 + |\theta _ j|)$](images/statug_nlmixed0270.png) .
.
-
For the forward-difference approximation of second-order derivatives that use only function calls and all central-difference formulas,
![$h_ j = \sqrt [3]{\eta } (1 + |\theta _ j|)$](images/statug_nlmixed0271.png) .
.
The value of ![]() is defined by the FDIGITS= option:
is defined by the FDIGITS= option: