The DISCRIM Procedure
Posterior Probability Error-Rate Estimates
The posterior probability error-rate estimates (Fukunaga and Kessel, 1973; Glick, 1978; Hora and Wilcox, 1982) for each group are based on the posterior probabilities of the observations classified into that same group.
A sample of observations with classification results can be used to estimate the posterior error rates. The following notation is used to describe the sample:
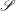
-
the set of observations in the (training) sample
- n
-
the number of observations in
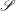
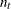
-
the number of observations in
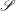 in group t
in group t
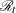
-
the set of observations such that the posterior probability belonging to group t is the largest
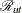
-
the set of observations from group u such that the posterior probability belonging to group t is the largest
The classification error rate for group t is defined as
|
|
The posterior probability of ![]() for group t can be written as
for group t can be written as
|
|
where ![]() is the unconditional density of
is the unconditional density of ![]() .
.
Thus, if you replace ![]() with
with ![]() , the error rate is
, the error rate is
|
|
An estimator of ![]() , unstratified over the groups from which the observations come, is then given by
, unstratified over the groups from which the observations come, is then given by
|
|
where ![]() is estimated from the classification criterion, and the summation is over all sample observations of
is estimated from the classification criterion, and the summation is over all sample observations of ![]() classified into group t. The true group membership of each observation is not required in the estimation. The term
classified into group t. The true group membership of each observation is not required in the estimation. The term ![]() is the number of observations that are expected to be classified into group t, given the priors. If more observations than expected are classified into group t, then
is the number of observations that are expected to be classified into group t, given the priors. If more observations than expected are classified into group t, then ![]() can be negative.
can be negative.
Further, if you replace ![]() with
with ![]() , the error rate can be written as
, the error rate can be written as
|
|
and an estimator stratified over the group from which the observations come is given by
|
|
The inner summation is over all sample observations of ![]() coming from group u and classified into group t, and
coming from group u and classified into group t, and ![]() is the number of observations originally from group u. The stratified estimate uses only the observations with known group membership. When the prior probabilities of the group
membership are proportional to the group sizes, the stratified estimate is the same as the unstratified estimator.
is the number of observations originally from group u. The stratified estimate uses only the observations with known group membership. When the prior probabilities of the group
membership are proportional to the group sizes, the stratified estimate is the same as the unstratified estimator.
The estimated group-specific error rates can be less than zero, usually due to a large discrepancy between prior probabilities of group membership and group sizes. To have a reliable estimate for group-specific error rate estimates, you should use group sizes that are at least approximately proportional to the prior probabilities of group membership.
A total error rate is defined as a weighted average of the individual group error rates
|
|
and can be estimated from
|
|
or
|
|
The total unstratified error-rate estimate can also be written as
|
|
which is one minus the average value of the maximum posterior probabilities for each observation in the sample. The prior probabilities of group membership do not appear explicitly in this overall estimate.
