The CANDISC Procedure
Computational Resources
In the following discussion, let
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Memory Requirements
The amount of memory in bytes for temporary storage needed to process the data is
|
|
With the ANOVA option, the temporary storage must be increased by 16v bytes. The DISTANCE option requires an additional temporary
storage of ![]() bytes.
bytes.
Time Requirements
The following factors determine the time requirements of the CANDISC procedure:
-
The time needed for reading the data and computing covariance matrices is proportional to
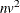 . PROC CANDISC must also look up each class level in the list. This is faster if the data are sorted by the CLASS variable.
The time for looking up class levels is proportional to a value ranging from n to
. PROC CANDISC must also look up each class level in the list. This is faster if the data are sorted by the CLASS variable.
The time for looking up class levels is proportional to a value ranging from n to 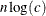 .
.
-
The time for inverting a covariance matrix is proportional to
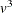 .
.
-
The time required for the canonical discriminant analysis is proportional to
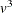 .
.
Each of the preceding factors has a different constant of proportionality.
