The FMM Procedure (Experimental)
Example 37.3 Enforcing Homogeneity Constraints: Count and Dispersion—It Is All Over!
The following example demonstrates how you can use either the EQUATE= option in the MODEL statement or the RESTRICT statement to impose homogeneity constraints on chosen model effects.
The data for this example were presented by Margolin, Kaplan, and Zeiger (1981) and analyzed by various authors applying a number of techniques. The following DATA step shows the number of revertant salmonella colonies (variable num) at six levels of quinoline dosing (variable dose). There are three replicate plates at each dose of quinoline.
data assay;
label dose = 'Dose of quinoline (microg/plate)'
num = 'Observed number of colonies';
input dose @;
logd = log(dose+10);
do i=1 to 3; input num@; output; end;
datalines;
0 15 21 29
10 16 18 21
33 16 26 33
100 27 41 60
333 33 38 41
1000 20 27 42
;
The basic notion is that the data are overdispersed relative to a Poisson distribution in which the logarithm of the mean count is modeled as a linear regression in dose (in 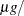 plate) and in the derived variable
plate) and in the derived variable 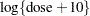 (Lawless 1987). The log of the expected count of revertants is thus
(Lawless 1987). The log of the expected count of revertants is thus
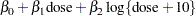 |
The following statements fit a standard Poisson regression model to these data:
proc fmm data=assay; model num = dose logd / dist=Poisson; run;
The Pearson statistic for this model is rather large compared to the number of degrees of freedom (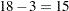 ). The ratio
). The ratio 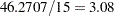 indicates an overdispersion problem in the Poisson model (Output 37.3.1).
indicates an overdispersion problem in the Poisson model (Output 37.3.1).
| Number of Observations Read | 18 |
|---|---|
| Number of Observations Used | 18 |
| Fit Statistics | |
|---|---|
| -2 Log Likelihood | 136.3 |
| AIC (smaller is better) | 142.3 |
| AICC (smaller is better) | 144.0 |
| BIC (smaller is better) | 144.9 |
| Pearson Statistic | 46.2707 |
| Parameter Estimates for 'Poisson' Model | ||||
|---|---|---|---|---|
| Effect | Estimate | Standard Error | z Value | Pr > |z| |
| Intercept | 2.1728 | 0.2184 | 9.95 | <.0001 |
| dose | -0.00101 | 0.000245 | -4.13 | <.0001 |
| logd | 0.3198 | 0.05700 | 5.61 | <.0001 |
Breslow (1984) accounts for overdispersion by including a random effect in the predictor for the log rate and applying a quasi-likelihood technique to estimate the parameters. Wang et al. (1996) examine these data using mixtures of Poisson regression models. They fit several two- and three-component Poisson regression mixtures. Examining the log likelihoods, AIC, and BIC criteria, they eventually settle on a two-component model in which the intercepts vary by category and the regression coefficients are the same. This mixture model can be written as
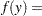 |
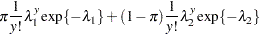 |
|||
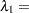 |
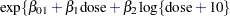 |
|||
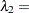 |
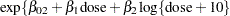 |
This model is fit with the FMM procedure with the following statements:
proc fmm data=assay;
model num = dose logd / dist=Poisson k=2
equate=effects(dose logd);
run;
The EQUATE= option in the MODEL statement places constraints on the optimization and makes the coefficients for dose and logd homogeneous across components in the model. Output 37.3.2 displays the "Fit Statistics" and parameter estimates in the mixture. The Pearson statistic is drastically reduced compared to the Poisson regression model in Output 37.3.1. With 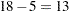 degrees of freedom, the ratio of the Pearson and the degrees of freedom is now
degrees of freedom, the ratio of the Pearson and the degrees of freedom is now 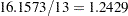 . Note that the effective number of parameters was used to compute the degrees of freedom, not the total number of parameters, because of the equality constraints.
. Note that the effective number of parameters was used to compute the degrees of freedom, not the total number of parameters, because of the equality constraints.
| Fit Statistics | |
|---|---|
| -2 Log Likelihood | 121.8 |
| AIC (smaller is better) | 131.8 |
| AICC (smaller is better) | 136.8 |
| BIC (smaller is better) | 136.3 |
| Pearson Statistic | 16.1573 |
| Effective Parameters | 5 |
| Effective Components | 2 |
| Parameter Estimates for 'Poisson' Model | |||||
|---|---|---|---|---|---|
| Component | Effect | Estimate | Standard Error | z Value | Pr > |z| |
| 1 | Intercept | 1.9097 | 0.2654 | 7.20 | <.0001 |
| 1 | dose | -0.00126 | 0.000273 | -4.62 | <.0001 |
| 1 | logd | 0.3639 | 0.06602 | 5.51 | <.0001 |
| 2 | Intercept | 2.4770 | 0.2731 | 9.07 | <.0001 |
| 2 | dose | -0.00126 | 0.000273 | -4.62 | <.0001 |
| 2 | logd | 0.3639 | 0.06602 | 5.51 | <.0001 |
| Parameter Estimates for Mixing Probabilities | |||||
|---|---|---|---|---|---|
| Effect | Linked Scale | Probability | |||
| Estimate | Standard Error | z Value | Pr > |z| | ||
| Intercept | 1.4984 | 0.6875 | 2.18 | 0.0293 | 0.8173 |
You could also have used RESTRICT statements to impose the homogeneity constraints on the model fit, as shown in the following statements:
proc fmm data=assay; model num = dose logd / dist=Poisson k=2; restrict 'common dose' dose 1, dose -1; restrict 'common logd' logd 1, logd -1; run;
The first RESTRICT statement equates the coefficients for the dose variable in the two components, and the second RESTRICT statement accomplishes the same for the coefficients of the logd variable. If the right-hand side of a restriction is not specified, PROC FMM defaults to equating the left-hand side of the restriction to zero. The "Linear Constraints" table in Output 37.3.3 shows that both linear equality constraints are active. The parameter estimates match the previous FMM run.
| Linear Constraints at Solution | |||||
|---|---|---|---|---|---|
| Label | k = 1 | k = 2 | Constraint Active |
||
| common dose | dose | - dose | = | 0 | Yes |
| common logd | logd | - logd | = | 0 | Yes |
| Parameter Estimates for 'Poisson' Model | |||||
|---|---|---|---|---|---|
| Component | Effect | Estimate | Standard Error | z Value | Pr > |z| |
| 1 | Intercept | 1.9097 | 0.2654 | 7.20 | <.0001 |
| 1 | dose | -0.00126 | 0.000273 | -4.62 | <.0001 |
| 1 | logd | 0.3639 | 0.06602 | 5.51 | <.0001 |
| 2 | Intercept | 2.4770 | 0.2731 | 9.07 | <.0001 |
| 2 | dose | -0.00126 | 0.000273 | -4.62 | <.0001 |
| 2 | logd | 0.3639 | 0.06602 | 5.51 | <.0001 |
| Parameter Estimates for Mixing Probabilities | |||||
|---|---|---|---|---|---|
| Effect | Linked Scale | Probability | |||
| Estimate | Standard Error | z Value | Pr > |z| | ||
| Intercept | 1.4984 | 0.6875 | 2.18 | 0.0293 | 0.8173 |
Wang et al. (1996) note that observation 12 with a revertant colony count of 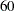 is comparably high. The following statements remove the observation from the analysis and fit their selected model:
is comparably high. The following statements remove the observation from the analysis and fit their selected model:
proc fmm data=assay(where=(num ne 60));
model num = dose logd / dist=Poisson k=2
equate=effects(dose logd);
run;
| Fit Statistics | |
|---|---|
| -2 Log Likelihood | 111.5 |
| AIC (smaller is better) | 121.5 |
| AICC (smaller is better) | 126.9 |
| BIC (smaller is better) | 125.6 |
| Pearson Statistic | 16.5987 |
| Effective Parameters | 5 |
| Effective Components | 2 |
| Parameter Estimates for 'Poisson' Model | |||||
|---|---|---|---|---|---|
| Component | Effect | Estimate | Standard Error | z Value | Pr > |z| |
| 1 | Intercept | 2.2272 | 0.3022 | 7.37 | <.0001 |
| 1 | dose | -0.00065 | 0.000445 | -1.46 | 0.1440 |
| 1 | logd | 0.2432 | 0.1045 | 2.33 | 0.0199 |
| 2 | Intercept | 2.5477 | 0.3331 | 7.65 | <.0001 |
| 2 | dose | -0.00065 | 0.000445 | -1.46 | 0.1440 |
| 2 | logd | 0.2432 | 0.1045 | 2.33 | 0.0199 |
| Parameter Estimates for Mixing Probabilities | |||||
|---|---|---|---|---|---|
| Effect | Linked Scale | Probability | |||
| Estimate | Standard Error | z Value | Pr > |z| | ||
| Intercept | 0.3134 | 1.7261 | 0.18 | 0.8559 | 0.5777 |
The ratio of Pearson Statistic over degrees of freedom (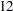 ) is only slightly worse than in the previous model; the loss of 5% of the observations carries a price (Output 37.3.4). The parameter estimates for the two intercepts are now fairly close. If the intercepts were identical, then the two-component model would collapse to the Poisson regression model:
) is only slightly worse than in the previous model; the loss of 5% of the observations carries a price (Output 37.3.4). The parameter estimates for the two intercepts are now fairly close. If the intercepts were identical, then the two-component model would collapse to the Poisson regression model:
proc fmm data=assay(where=(num ne 60)); model num = dose logd / dist=Poisson; run;
| Number of Observations Read | 17 |
|---|---|
| Number of Observations Used | 17 |
| Fit Statistics | |
|---|---|
| -2 Log Likelihood | 114.1 |
| AIC (smaller is better) | 120.1 |
| AICC (smaller is better) | 121.9 |
| BIC (smaller is better) | 122.5 |
| Pearson Statistic | 27.8008 |
| Parameter Estimates for 'Poisson' Model | ||||
|---|---|---|---|---|
| Effect | Estimate | Standard Error | z Value | Pr > |z| |
| Intercept | 2.3164 | 0.2244 | 10.32 | <.0001 |
| dose | -0.00072 | 0.000258 | -2.78 | 0.0055 |
| logd | 0.2603 | 0.05996 | 4.34 | <.0001 |
Compared to the same model applied to the full data, the Pearson statistic is much reduced (compare 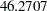 in Output 37.3.1 to
in Output 37.3.1 to 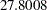 in Output 37.3.5). The outlier—or overcount, if you will—induces at least some of the overdispersion.
in Output 37.3.5). The outlier—or overcount, if you will—induces at least some of the overdispersion.
