Taylor Series Linearization

The Taylor series linearization method is the default variance estimation method used by PROC SURVEYPHREG. See the section Notation and Estimation for definitions of the notation used in this section. Let

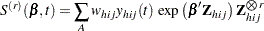where 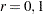. Let 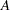be the set of indices in the selected sample. Let

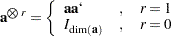and let 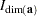be the identity matrix of appropriate dimension.

Let 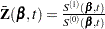. The score residual for the 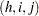th subject is

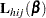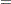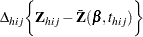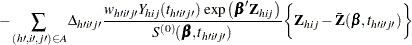For TIES=EFRON, the computation of the score residuals is modified to comply with the Efron partial likelihood. See the section Residuals for more information.

The Taylor series estimate of the covariance matrix of 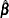is

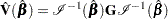where is the observed information matrix and the 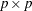matrix 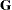is defined as

The observed residuals, their sums and means are defined as follows:

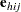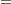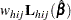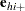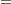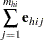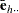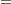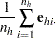The factor 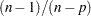in the computation of the matrix 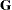reduces the small sample bias that is associated with using the estimated function to calculate deviations (Fuller et al. (1989), pp. 77–81). For simple random sampling, this factor contributes to the degrees of freedom correction applied to the residual mean square for ordinary least squares in which 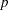parameters are estimated. By default, the procedure uses this adjustment in the variance estimation. If you do not want to use this multiplier in the variance estimator, then specify the VADJUST=NONE option in the MODEL statement.