| The SURVEYLOGISTIC Procedure |
Taylor Series (Linearization)
The Taylor series (linearization) method is the most commonly used method to estimate the covariance matrix of the regression coefficients for complex survey data. It is the default variance estimation method used by PROC SURVEYLOGISTIC.
Using the notation described in the section Notation, the estimated covariance matrix of model parameters 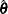 by the Taylor series method is
by the Taylor series method is
 |
where
 |
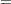 |
 |
|||
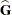 |
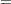 |
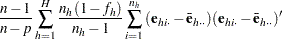 |
|||
 |
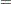 |
 |
|||
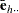 |
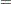 |
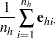 |
and 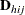 is the matrix of partial derivatives of the link function
is the matrix of partial derivatives of the link function 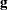 with respect to
with respect to 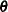 and
and 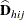 and the response probabilities
and the response probabilities 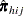 are evaluated at
are evaluated at 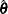 .
.
If you specify the TECHNIQUE=NEWTON option in the MODEL statement to request the Newton-Raphson algorithm, the matrix  is replaced by the negative (expected) Hessian matrix when the estimated covariance matrix
is replaced by the negative (expected) Hessian matrix when the estimated covariance matrix 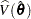 is computed.
is computed.
Adjustments to the Variance Estimation
The factor 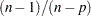 in the computation of the matrix
in the computation of the matrix 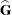 reduces the small sample bias associated with using the estimated function to calculate deviations (Morel 1989; Hidiroglou, Fuller, and Hickman 1980). For simple random sampling, this factor contributes to the degrees-of-freedom correction applied to the residual mean square for ordinary least squares in which
reduces the small sample bias associated with using the estimated function to calculate deviations (Morel 1989; Hidiroglou, Fuller, and Hickman 1980). For simple random sampling, this factor contributes to the degrees-of-freedom correction applied to the residual mean square for ordinary least squares in which 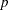 parameters are estimated. By default, the procedure uses this adjustment in Taylor series variance estimation. It is equivalent to specifying the VADJUST=DF option in the MODEL statement. If you do not want to use this multiplier in the variance estimation, you can specify the VADJUST=NONE option in the MODEL statement to suppress this factor.
parameters are estimated. By default, the procedure uses this adjustment in Taylor series variance estimation. It is equivalent to specifying the VADJUST=DF option in the MODEL statement. If you do not want to use this multiplier in the variance estimation, you can specify the VADJUST=NONE option in the MODEL statement to suppress this factor.
In addition, you can specify the VADJUST=MOREL option to request an adjustment to the variance estimator for the model parameters 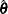 , introduced by Morel (1989):
, introduced by Morel (1989):
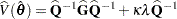 |
where for given nonnegative constants 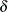 and
and 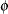 ,
,
 |
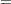 |
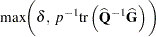 |
|||
 |
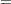 |
 |
The adjustment 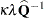 does the following:
does the following:
reduces the small sample bias reflected in inflated Type I error rates
guarantees a positive-definite estimated covariance matrix provided that
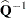 exists
exists is close to zero when the sample size becomes large
In this adjustment,  is an estimate of the design effect, which has been bounded below by the positive constant
is an estimate of the design effect, which has been bounded below by the positive constant 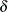 . You can use DEFFBOUND=
. You can use DEFFBOUND=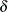 in the VADJUST=MOREL option in the MODEL statement to specify this lower bound; by default, the procedure uses
in the VADJUST=MOREL option in the MODEL statement to specify this lower bound; by default, the procedure uses 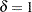 . The factor
. The factor 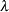 converges to zero when the sample size becomes large, and
converges to zero when the sample size becomes large, and 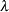 has an upper bound
has an upper bound 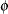 . You can use ADJBOUND=
. You can use ADJBOUND=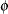 in the VADJUST=MOREL option in the MODEL statement to specify this upper bound; by default, the procedure uses
in the VADJUST=MOREL option in the MODEL statement to specify this upper bound; by default, the procedure uses 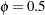 .
.
Copyright © SAS Institute, Inc. All Rights Reserved.