| The MCMC Procedure |
| Multivariate Density Functions |
The DATA step has functions that compute the logarithm of the density of some multivariate distributions. You can use them in PROC MCMC. For a complete listing of multivariate functions, see SAS Language Reference: Dictionary.
Some commonly used multivariate functions in Bayesian analysis are as follows:
LOGMPDFNORMAL, the logarithm of the multivariate normal
LOGMPDFWISHART, the logarithm of the Wishart
LOGMPDFIWISHART, the logarithm of the inverted-Wishart
LOGMPDFDIR1, the logarithm of the Dirichlet distribution of Type I
LOGMPDFDIR2, the logarithm of the Dirichlet distribution of Type II
LOGMPDFMULTINOM, the logarithm of the multinomial
Other multivariate density functions include: LOGMPDFT (t-distribution), LOGMPDFGAMMA (gamma distribution), LOGMPDFBETA1 (beta of type I), and LOGMPDFBETA2 (beta of type II).
Density Function Definition
LOGMPDFNORMAL
Let  be an
be an  -dimensional random vector with mean vector
-dimensional random vector with mean vector 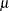 and covariance matrix
and covariance matrix 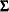 . The density is
. The density is
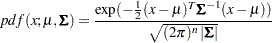 |
where 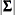 is the determinant of the covariance matrix
is the determinant of the covariance matrix 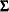 .
.
The function has syntax:
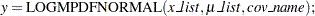 |
Warning:you must set up the 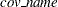 covariance matrix before using the LOGMPDFNORMAL function and free the memory after PROC MCMC exits. See the section Set Up the Covariance Matrices and Free Memory.
covariance matrix before using the LOGMPDFNORMAL function and free the memory after PROC MCMC exits. See the section Set Up the Covariance Matrices and Free Memory.
LOGMPDFWISHART and LOGMPDFIWISHART
The density function from the Wishart distribution is:
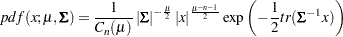 |
with  , and the trace of a square matrix
, and the trace of a square matrix 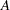 is given by:
is given by:
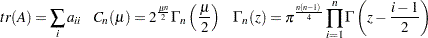 |
The density function from the inverse-Wishart distribution is:
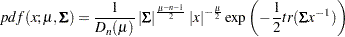 |
for  , and
, and
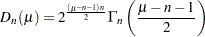 |
If 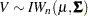 then
then 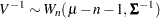
The functions have syntax:
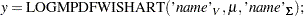 |
and for the inverted Wishart:
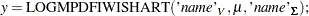 |
The three arguments are the multivariate matrix 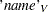 , the degrees of freedom
, the degrees of freedom 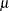 , and the covariance matrix
, and the covariance matrix 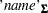 k
k
Warning:you must set up the 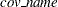 covariance matrix before using these functions and free the memory after PROC MCMC exits. See the section Set Up the Covariance Matrices and Free Memory.
covariance matrix before using these functions and free the memory after PROC MCMC exits. See the section Set Up the Covariance Matrices and Free Memory.
LOGMPDFDIR1 and LOGMPDFDIR2
The random variables 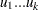 , with
, with 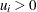 and
and 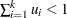 , are said to have a Dirichlet Type I distribution with parameters
, are said to have a Dirichlet Type I distribution with parameters 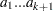 if their joint pdf is given by:
if their joint pdf is given by:
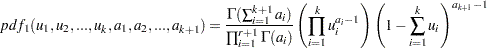 |
The variables are said to have a Dirichlet type II distribution with parameters 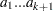 if their joint pdf is given by the following:
if their joint pdf is given by the following:
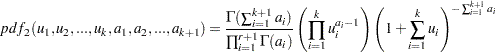 |
The functions have syntax:
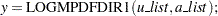 |
and
 |
LOGMPDFMULTINOM
Let  be random variables that denote the number of occurring of the events
be random variables that denote the number of occurring of the events 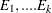 respectively occurring with probabilities
respectively occurring with probabilities  . Let
. Let 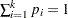 and let
and let 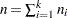 . Then the joint distribution of
. Then the joint distribution of 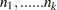 is the following:
is the following:
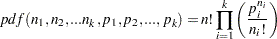 |
The function has syntax:
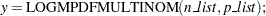 |
Set Up the Covariance Matrices and Free Memory
For distributions that require symmetric positive definite matrices, such as the LOGMPDFNORMAL, LOGMPDFWISHART and LOGMPDFIWISHART functions, you need to set up these matrices by using the following functions:
Use LOGMPDFSETSQ to set up a symmetric positive definite matrix from all its elements:
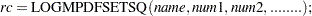
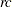 is set to
is set to 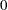 when the numeric arguments describe a symmetric positive definite matrix, otherwise it is set to a nonzero value.
when the numeric arguments describe a symmetric positive definite matrix, otherwise it is set to a nonzero value. Use LOGMPDFSET to set up a symmetric positive definite matrix from its lower triangular elements:
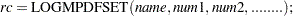
When the numeric arguments describe a symmetric positive definite matrix, the returned value
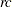 is set to
is set to 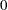 . Otherwise, a nonzero value for
. Otherwise, a nonzero value for 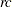 is returned.
is returned. Use LOGMPFFREE to free the workspace previously allocated with either LOGMPDFSET or LOGMPDFSETSQ:
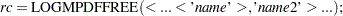
When called without arguments, the LOGMPDFFREE frees all the symbols previously allocated by LOGMPDFSETSQ or LOGMPDFSET. Each freed symbol is reported back in the SAS log.
The parameters used in these functions are defined as follows:
is a string containing the name of the work space that stores the matrix by the numeric parameters
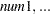 .
. are numeric arguments that represent the elements of a symmetric positive definite matrix.
You would set up this matrix under the DATA step by using the following syntax:
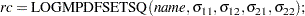 |
or the syntax:
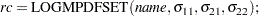 |
If the matrix is positive definite, the returned value 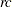 is zero.
is zero.
Copyright © SAS Institute, Inc. All Rights Reserved.