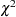PROC MCMC: Using Density Functions in the Programming Statements

The MCMC Procedure

Using Density Functions in the Programming Statements

Density Functions in PROC MCMC

PROC MCMC also has a number of internally defined log-density functions. The functions have the basic form of lpdfdist(x, parm-list, <lower>, <upper>), where dist is the name of the distribution (see Table 52.31). The argument x is the random variable, parm-list is the list of parameters, and lower and upper are boundary arguments. The lower and upper arguments are optional but positional. With the exception of the Bernoulli and uniform distribution, you can specify limits on all distributions.

To set a lower bound on the normal density:

lpdfnorm(x, 0, 1, -2);

To set just an upper bound, specify a missing value for the lower bound argument:

lpdfnorm(x, 0, 1, ., 2);

Leaving both limits out gives you the unbounded density, and you can also specify both bounds:

lpdfnorm(x, 0, 1);
lpdfnorm(x, 0, 1, -3, 4);

See the following table for a list of distributions and their corresponding lpdf functions.

Table 52.31 Logarithm of Density Functions in PROC MCMC
Distribution Name	Function Call
beta	`lpdfbeta(x, a, b, <lower>, <upper>);`
binary	`lpdfbern(x, p);`
binomial	`lpdfbin(x, n, p, <lower>, <upper>);`
Cauchy	`lpdfcau(x, loc, scale, <lower>, <upper>);`
$\text{[math]}$	`lpdfchisq(x, df, <lower>, <upper>);`
exponential $\text{[math]}$	`lpdfechisq(x, df, <lower>, <upper>);`
exponential gamma	`lpdfegamma(x, sp, scale, <lower>, <upper>);`
exponential exponential	`lpdfeexpon(x, scale, <lower>, <upper>);`
exponential inverse $\text{[math]}$	`lpdfeichisq(x, df, <lower>, <upper>);`
exponential inverse-gamma	`lpdfeigamma(x, sp, scale, <lower>, <upper>);`
exponential scaled inverse $\text{[math]}$	`lpdfesichisq(x, df, scale, <lower>, <upper>);`
exponential	`lpdfexpon(x, scale, <lower>, <upper>);`
gamma	`lpdfgamma(x, sp, scale, <lower>, <upper>);`
geometric	`lpdfgeo(x, p, <lower>, <upper>);`
inverse $\text{[math]}$	`lpdfichisq(x, df, <lower>, <upper>);`
inverse-gamma	`lpdfigamma(x, sp, scale, <lower>, <upper>);`
Laplace	`lpdfdexp(x, loc, scale, <lower>, <upper>);`
logistic	`lpdflogis(x, loc, scale, <lower>, <upper>);`
lognormal	`lpdflnorm(x, loc, sd, <lower>, <upper>);`
negative binomial	`lpdfnegbin(x, n, p, <lower>, <upper>);`
normal	`lpdfnorm(x, mu, sd, <lower>, <upper>);`
Pareto	`lpdfpareto(x, sp, scale, <lower>, <upper>);`
Poisson	`lpdfpoi(x, mean, <lower>, <upper>);`
scaled inverse $\text{[math]}$	`lpdfsichisq(x, df, scale, <lower>, <upper>);`
T	`lpdft(x, mu, sd, df, <lower>, <upper>);`
uniform	`lpdfunif(x, a, b);`
Wald	`lpdfwald(x, mean, scale, <lower>, <upper>);`
Weibull	`lpdfwei(x, loc, sp, scale, <lower>, <upper>);`

Standard Distributions, the logpdf Functions, and the lpdfdist Functions

Standard distributions listed in the section Standard Distributions are names only, and they can only be used in the MODEL, PRIOR, and HYPERPRIOR statements to specify either a prior distribution or a conditional distribution of the data given parameters. They do not return any values, and you cannot use them in the programming statements.

The LOGPDF functions are DATA step functions that compute the logarithm of various probability density (mass) functions. For example, logpdf("beta", x, 2, 15) returns the log of a beta density with parameters a = 2 and b = 15, evaluated at $\text{[math]}$ . All the LOGPDF functions are supported in PROC MCMC.

The lpdfdist functions are unique to PROC MCMC. They compute the logarithm of various probability density (mass) functions. The functions are the same as the LOGPDF functions when it comes to calculating the log density. For example, lpdfbeta(x, 2, 15) returns the same value as logpdf("beta", x, 2, 15). The lpdfdist functions cover a greater class of probability density functions, and they take the optional but positional boundary arguments. There are no corresponding lcdfdist or lsdfdist functions in PROC MCMC. To work with the cumulative probability function or the survival functions, you need to use the LOGCDF and the LOGSDF DATA step functions.

Top of Page