| The HPMIXED Procedure |
Example 43.2 Comparing Results from PROC HPMIXED and PROC MIXED
This example revisits the mixed model problem from the section Getting Started: MIXED Procedure, in Chapter 56, The MIXED Procedure, with the data set shown in the following statements:
data heights; input Family Gender$ Height @@; datalines; 1 F 67 1 F 66 1 F 64 1 M 71 1 M 72 2 F 63 2 F 63 2 F 67 2 M 69 2 M 68 2 M 70 3 F 63 3 M 64 4 F 67 4 F 66 4 M 67 4 M 67 4 M 69 ;
The response variable Height measures the heights (in inches) of 18 individuals. The individuals are classified according to Family and Gender. The following statements fit a mixed model with random effects for Family and the Family*Gender interaction with the MIXED procedure:
proc mixed; class Family Gender; model Height = Gender / s; random Family Family*Gender / s; run;
The "Iteration History" and "Fit Statistics" tables for the optimization in PROC MIXED are shown in Output 43.2.1. The MIXED procedure converges after six iterations and achieves a –2 restricted log likelihood of  .
.
Output 43.2.2 displays the covariance parameter estimates and the solutions for the fixed and random effects. Because the fixed-effect model contains a classification effect (Gender) and an intercept, the  matrix is singular. Only two fixed-effect parameters can be estimated in this model. The MIXED procedure, relying on a sweep operation in the order in which effects enter the model, determines that the last column of the
matrix is singular. Only two fixed-effect parameters can be estimated in this model. The MIXED procedure, relying on a sweep operation in the order in which effects enter the model, determines that the last column of the  matrix is a linear function of previous columns. Consequently, the coefficient for the second level of the Gender variable is zero.
matrix is a linear function of previous columns. Consequently, the coefficient for the second level of the Gender variable is zero.
| Solution for Fixed Effects | ||||||
|---|---|---|---|---|---|---|
| Effect | Gender | Estimate | Standard Error | DF | t Value | Pr > |t| |
| Intercept | 68.2114 | 1.1477 | 3 | 59.43 | <.0001 | |
| Gender | F | -3.3621 | 1.1923 | 3 | -2.82 | 0.0667 |
| Gender | M | 0 | . | . | . | . |
| Solution for Random Effects | |||||||
|---|---|---|---|---|---|---|---|
| Effect | Gender | Family | Estimate | Std Err Pred | DF | t Value | Pr > |t| |
| Family | 1 | 1.2680 | 1.1201 | 10 | 1.13 | 0.2840 | |
| Family | 2 | 0.08980 | 1.1121 | 10 | 0.08 | 0.9372 | |
| Family | 3 | -1.6660 | 1.1712 | 10 | -1.42 | 0.1853 | |
| Family | 4 | 0.3082 | 1.1201 | 10 | 0.28 | 0.7888 | |
| Family*Gender | F | 1 | -0.3198 | 1.0810 | 10 | -0.30 | 0.7734 |
| Family*Gender | M | 1 | 1.2523 | 1.0933 | 10 | 1.15 | 0.2787 |
| Family*Gender | F | 2 | -0.4299 | 1.0774 | 10 | -0.40 | 0.6983 |
| Family*Gender | M | 2 | 0.4959 | 1.0774 | 10 | 0.46 | 0.6551 |
| Family*Gender | F | 3 | -0.08229 | 1.1409 | 10 | -0.07 | 0.9439 |
| Family*Gender | M | 3 | -1.1429 | 1.1409 | 10 | -1.00 | 0.3401 |
| Family*Gender | F | 4 | 0.8320 | 1.0933 | 10 | 0.76 | 0.4642 |
| Family*Gender | M | 4 | -0.6053 | 1.0810 | 10 | -0.56 | 0.5878 |
The "Type 3 Tests of Fixed Effects" table in Output 43.2.3 is produced by the MIXED procedure by default.
The same linear mixed model is fit with the HPMIXED procedure with the following statements:
proc hpmixed; class Family Gender; model Height = Gender / s; random Family Family*Gender / s; test gender; run;
Output 43.2.4 displays the "Iteration History" and "Fit Statistics" tables. The HPMIXED procedure, with its default quasi-Newton algorithm, achieves the same –2 restricted log likelihood as the MIXED procedure ( ; see Output 43.2.1).
; see Output 43.2.1).
Output 43.2.5 displays the results that correspond to those in Output 43.2.2 in the MIXED procedure.
| Solution for Fixed Effects | ||||||
|---|---|---|---|---|---|---|
| Effect | Gender | Estimate | Standard Error | DF | t Value | Pr > |t| |
| Intercept | 0 | . | . | . | . | |
| Gender | F | 64.8493 | 1.1477 | 16 | 56.50 | <.0001 |
| Gender | M | 68.2114 | 1.1477 | 16 | 59.43 | <.0001 |
| Solution for Random Effects | |||||||
|---|---|---|---|---|---|---|---|
| Effect | Gender | Family | Estimate | Std Err Pred | DF | t Value | Pr > |t| |
| Family | 1 | 1.2680 | 1.1201 | 16 | 1.13 | 0.2743 | |
| Family | 2 | 0.08980 | 1.1121 | 16 | 0.08 | 0.9366 | |
| Family | 3 | -1.6660 | 1.1712 | 16 | -1.42 | 0.1741 | |
| Family | 4 | 0.3082 | 1.1201 | 16 | 0.28 | 0.7867 | |
| Family*Gender | F | 1 | -0.3198 | 1.0810 | 16 | -0.30 | 0.7712 |
| Family*Gender | M | 1 | 1.2523 | 1.0933 | 16 | 1.15 | 0.2689 |
| Family*Gender | F | 2 | -0.4299 | 1.0774 | 16 | -0.40 | 0.6951 |
| Family*Gender | M | 2 | 0.4959 | 1.0774 | 16 | 0.46 | 0.6515 |
| Family*Gender | F | 3 | -0.08229 | 1.1409 | 16 | -0.07 | 0.9434 |
| Family*Gender | M | 3 | -1.1429 | 1.1409 | 16 | -1.00 | 0.3314 |
| Family*Gender | F | 4 | 0.8320 | 1.0933 | 16 | 0.76 | 0.4577 |
| Family*Gender | M | 4 | -0.6053 | 1.0810 | 16 | -0.56 | 0.5832 |
A number of points are noteworthy in comparing the results from the procedures. The covariance parameter estimates are the same, yet the solutions for the fixed effects differ. In fact, both solutions are correct. Solving a sparse system of linear equations requires reordering of the mixed model equations to minimize memory consumption in the factorization process. As a consequence, the order in which singularities are detected can differ from the order in which effects enter the model. Mathematically, the two sets of solutions simply correspond to different choices for the generalized inverse in solving a singular linear system. See the sections Generalized Inverse Matrices and Linear Model Theory, in Chapter 3, Introduction to Statistical Modeling with SAS/STAT Software, for more information about the role and importance of generalized inverses in linear model analysis.
Although the two sets of solutions for the fixed effects correspond to different choices of generalized inverses, many important results are invariant to the choice of the 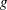 -inverse. For example, the solutions for the random effects in Output 43.2.5 and Output 43.2.2 are identical. Also, the test for the Gender effect yields the same F value in both analyses (compare Output 43.2.6 and Output 43.2.3). However, note that the p-values associated with both F tests and t tests differ between the two procedures. This is due to their different default methods for computing the degrees of freedom. For this model, the HPMIXED procedure use the residual method to determine the denominator degrees of freedom for tests of fixed effects, whereas the MIXED procedure uses the containment method. The containment method is order-dependent, and thus not available in the HPMIXED procedure.
-inverse. For example, the solutions for the random effects in Output 43.2.5 and Output 43.2.2 are identical. Also, the test for the Gender effect yields the same F value in both analyses (compare Output 43.2.6 and Output 43.2.3). However, note that the p-values associated with both F tests and t tests differ between the two procedures. This is due to their different default methods for computing the degrees of freedom. For this model, the HPMIXED procedure use the residual method to determine the denominator degrees of freedom for tests of fixed effects, whereas the MIXED procedure uses the containment method. The containment method is order-dependent, and thus not available in the HPMIXED procedure.
Copyright © SAS Institute, Inc. All Rights Reserved.