| The GLM Procedure |
| Absorption |
Absorption is a computational technique used to reduce computing resource needs in certain cases. The classic use of absorption occurs when a blocking factor with a large number of levels is a term in the model.
For example, the statements
proc glm; absorb herd; class a b; model y=a b a*b; run;
are equivalent to
proc glm; class herd a b; model y=herd a b a*b; run;
The exception to the previous statements is that the Type II, Type III, or Type IV SS for HERD are not computed when HERD is absorbed.
The algorithm for absorbing variables is similar to the one used by the NESTED procedure for computing a nested analysis of variance. As each new row of  (corresponding to the nonabsorbed independent effects and the dependent variables) is constructed, it is adjusted for the absorbed effects in a Type I fashion. The efficiency of the absorption technique is due to the fact that this adjustment can be done in one pass of the data and without solving any linear equations, assuming that the data have been sorted by the absorbed variables.
(corresponding to the nonabsorbed independent effects and the dependent variables) is constructed, it is adjusted for the absorbed effects in a Type I fashion. The efficiency of the absorption technique is due to the fact that this adjustment can be done in one pass of the data and without solving any linear equations, assuming that the data have been sorted by the absorbed variables.
Several effects can be absorbed at one time. For example, these statements
proc glm; absorb herd cow; class a b; model y=a b a*b; run;
are equivalent to
proc glm; class herd cow a b; model y=herd cow(herd) a b a*b; run;
When you use absorption, the size of the 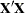 matrix is a function only of the effects in the MODEL statement. The effects being absorbed do not contribute to the size of the
matrix is a function only of the effects in the MODEL statement. The effects being absorbed do not contribute to the size of the 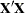 matrix.
matrix.
For the preceding example, a and b can be absorbed:
proc glm; absorb a b; class herd cow; model y=herd cow(herd); run;
Although the sources of variation in the results are listed as
a b(a) herd cow(herd)
all types of estimable functions for herd and cow(herd) are free of a, b, and a*b parameters.
To illustrate the savings in computing by using the ABSORB statement, PROC GLM is run on generated data with 1147 degrees of freedom in the model with the following statements.
data a;
do herd=1 to 40;
do cow=1 to 30;
do treatment=1 to 3;
do rep=1 to 2;
y = herd/5 + cow/10 + treatment + rannor(1);
output;
end;
end;
end;
end;
run;
proc glm data=a; class herd cow treatment; model y=herd cow(herd) treatment; run;
This analysis would have required over 6 megabytes of memory for the 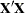 matrix had PROC GLM solved it directly. However, in the following statements, the GLM procedure needs only a
matrix had PROC GLM solved it directly. However, in the following statements, the GLM procedure needs only a  matrix for the intercept and treatment because the other effects are absorbed.
matrix for the intercept and treatment because the other effects are absorbed.
proc glm data=a; absorb herd cow; class treatment; model y = treatment; run;
These statements produce the results shown in Figure 39.17.
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 1201 | 49465.40242 | 41.18685 | 41.57 | <.0001 |
| Error | 5998 | 5942.23647 | 0.99070 | ||
| Corrected Total | 7199 | 55407.63889 |
Copyright © SAS Institute, Inc. All Rights Reserved.