Means versus LS-Means

Computing and comparing arithmetic means—either simple or weighted within-group averages of the input data—is a familiar and well-studied statistical process. This is the right approach to summarizing and comparing groups for one-way and balanced designs. However, in unbalanced designs with more than one effect, the arithmetic mean for a group might not accurately reflect the "typical" response for that group, since it does not take other effects into account.

For example, the following analysis of an unbalanced two-way design produces the ANOVA, means, and LS-means shown in Figure 39.18, Figure 39.19, and Figure 39.20.

data twoway;
   input Treatment Block y @@;
   datalines;
1 1 17   1 1 28   1 1 19   1 1 21   1 1 19
1 2 43   1 2 30   1 2 39   1 2 44   1 2 44
1 3 16
2 1 21   2 1 21   2 1 24   2 1 25
2 2 39   2 2 45   2 2 42   2 2 47
2 3 19   2 3 22   2 3 16
3 1 22   3 1 30   3 1 33   3 1 31
3 2 46
3 3 26   3 3 31   3 3 26   3 3 33   3 3 29   3 3 25
;

title "Unbalanced Two-way Design";
ods select ModelANOVA Means LSMeans;
 
proc glm data=twoway;
   class Treatment Block;
   model y = Treatment|Block;
   means Treatment;
   lsmeans Treatment;
run;
 
ods select all;

No matter how you look at them, these data exhibit a strong effect due to the blocks (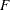 test ) and no significant interaction between treatments and blocks (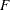 test ). 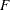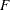But the lack of balance affects how the treatment effect is interpreted: in a main-effects-only model, there are no significant differences between the treatment means themselves (Type I test ), but there are highly significant differences between the treatment means corrected for the block effects (Type III test ).

LS-means are, in effect, within-group means appropriately adjusted for the other effects in the model. More precisely, they estimate the marginal means for a balanced population (as opposed to the unbalanced design). For this reason, they are also called estimated population marginal means by Searle, Speed, and Milliken (1980). In the same way that the Type I 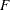test assesses differences between the arithmetic treatment means (when the treatment effect comes first in the model), the Type III 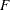test assesses differences between the LS-means. Accordingly, for the unbalanced two-way design, the discrepancy between the Type I and Type III tests is reflected in the arithmetic treatment means and treatment LS-means, as shown in Figure 39.19 and Figure 39.20. See the section Construction of Least Squares Means for more on LS-means.

Note that, while the arithmetic means are always uncorrelated (under the usual assumptions for analysis of variance), the LS-means might not be. This fact complicates the problem of multiple comparisons for LS-means; see the following section.