| The GLIMMIX Procedure |
Example 38.12 Fitting a Marginal (GEE-Type) Model
A marginal GEE-type model for clustered data is a model for correlated data that is specified through a mean function, a variance function, and a "working" covariance structure. Because the assumed covariance structure can be wrong, the covariance matrix of the parameter estimates is not based on the model alone. Rather, one of the empirical ("sandwich") estimators is used to make inferences robust against the choice of working covariance structure. PROC GLIMMIX can fit marginal models by using R-side random effects and drawing on the distributional specification in the MODEL statement to derive the link and variance functions. The EMPIRICAL= option in the PROC GLIMMIX statement enables you to choose one of a number of empirical covariance estimators.
The data for this example are from Thall and Vail (1990) and reflect the number of seizures of patients suffering fom epileptic episodes. After an eight-week period without treatment, patients were observed four times in two-week intervals during which they received a placebo or the drug Progabide in addition to other therapy. These data are also analyzed in Example 37.7 of Chapter 37, The GENMOD Procedure. The following DATA step creates the data set seizures. The variable id identifies the subjects in the study, and the variable trt identifies whether a subject received the placebo (trt = 0) or the drug Progabide (trt = 1). The variable x1 takes on value 0 for the baseline measurement and 1 otherwise.
data seizures;
array c{5};
input id trt c1-c5;
do i=1 to 5;
x1 = (i > 1);
ltime = (i=1)*log(8) + (i ne 1)*log(2);
cnt = c{i};
output;
end;
keep id cnt x1 trt ltime;
datalines;
101 1 76 11 14 9 8
102 1 38 8 7 9 4
103 1 19 0 4 3 0
104 0 11 5 3 3 3
106 0 11 3 5 3 3
107 0 6 2 4 0 5
108 1 10 3 6 1 3
110 1 19 2 6 7 4
111 1 24 4 3 1 3
112 1 31 22 17 19 16
113 1 14 5 4 7 4
114 0 8 4 4 1 4
116 0 66 7 18 9 21
117 1 11 2 4 0 4
118 0 27 5 2 8 7
121 1 67 3 7 7 7
122 1 41 4 18 2 5
123 0 12 6 4 0 2
124 1 7 2 1 1 0
126 0 52 40 20 23 12
128 1 22 0 2 4 0
129 1 13 5 4 0 3
130 0 23 5 6 6 5
135 0 10 14 13 6 0
137 1 46 11 14 25 15
139 1 36 10 5 3 8
141 0 52 26 12 6 22
143 1 38 19 7 6 7
145 0 33 12 6 8 4
147 1 7 1 1 2 3
201 0 18 4 4 6 2
202 0 42 7 9 12 14
203 1 36 6 10 8 8
204 1 11 2 1 0 0
205 0 87 16 24 10 9
206 0 50 11 0 0 5
208 1 22 4 3 2 4
209 1 41 8 6 5 7
210 0 18 0 0 3 3
211 1 32 1 3 1 5
213 0 111 37 29 28 29
214 1 56 18 11 28 13
215 0 18 3 5 2 5
217 0 20 3 0 6 7
218 1 24 6 3 4 0
219 0 12 3 4 3 4
220 0 9 3 4 3 4
221 1 16 3 5 4 3
222 0 17 2 3 3 5
225 1 22 1 23 19 8
226 0 28 8 12 2 8
227 0 55 18 24 76 25
228 1 25 2 3 0 1
230 0 9 2 1 2 1
232 1 13 0 0 0 0
234 0 10 3 1 4 2
236 1 12 1 4 3 2
238 0 47 13 15 13 12
;
The model fit initially with the following PROC GLIMMIX statements is a Poisson generalized linear model with effects for an intercept, the baseline measurement, the treatment, and their interaction:
proc glimmix data=seizures;
model cnt = x1 trt x1*trt / dist=poisson offset=ltime
ddfm=none s;
run;
The DDFM=NONE option is chosen in the MODEL statement to produce chi-square and z tests instead of F and t tests.
Because the initial pretreatment time period is four times as long as the subsequent measurement intervals, an offset variable is used to standardize the counts. If 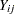 denotes the number of seizures of subject
denotes the number of seizures of subject 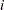 in time interval
in time interval 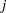 of length
of length  , then
, then 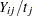 is the number of seizures per time unit. Modeling the average number per time unit with a log link leads to
is the number of seizures per time unit. Modeling the average number per time unit with a log link leads to 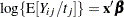 or
or  . The logarithm of time (variable ltime) thus serves as an offset. Suppose that
. The logarithm of time (variable ltime) thus serves as an offset. Suppose that 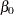 denotes the intercept,
denotes the intercept,  the effect of x1, and
the effect of x1, and  the effect of trt. Then
the effect of trt. Then 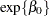 is the expected number of seizures per week in the placebo group at baseline. The corresponding numbers in the treatment group are
is the expected number of seizures per week in the placebo group at baseline. The corresponding numbers in the treatment group are  at baseline and
at baseline and  for postbaseline visits.
for postbaseline visits.
The "Model Information" table shows that the parameters in this Poisson model are estimated by maximum likelihood (Output 38.12.1). In addition to the default link and variance function, the variable ltime is used as an offset.
Fit statistics and parameter estimates are shown in Output 38.12.2.
Because this is a generalized linear model, the large value for the ratio of the Pearson chi-square statistic and its degrees of freedom is indicative of a model shortcoming. The data are considerably more dispersed than is expected under a Poisson model. There could be many reasons for this overdispersion—for example, a misspecified mean model, data that might not be Poisson distributed, an incorrect variance function, and correlations among the observations. Because these data are repeated measurements, the presence of correlations among the observations from the same subject is a likely contributor to the overdispersion.
The following PROC GLIMMIX statements fit a marginal model with correlations. The model is a marginal one, because no G-side random effects are specified on which the distribution could be conditioned. The choice of the id variable as the SUBJECT effect indicates that observations from different IDs are uncorrelated. Observations from the same ID are assumed to follow a compound symmetry (equicorrelation) model. The EMPIRICAL option in the PROC GLIMMIX statement requests the classical sandwich estimator as the covariance estimator for the fixed effects:
proc glimmix data=seizures empirical;
class id;
model cnt = x1 trt x1*trt / dist=poisson offset=ltime
ddfm=none covb s;
random _residual_ / subject=id type=cs vcorr;
run;
The "Model Information" table shows that the parameters are now estimated by residual pseudo-likelihood (compare Output 38.12.3 and Output 38.12.1). And in this fact lies the main difference between fitting marginal models with PROC GLIMMIX and with GEE methods as per Liang and Zeger (1986), where parameters of the working correlation matrix are estimated by the method of moments.
| Model Information | |
|---|---|
| Data Set | WORK.SEIZURES |
| Response Variable | cnt |
| Response Distribution | Poisson |
| Link Function | Log |
| Variance Function | Default |
| Offset Variable | ltime |
| Variance Matrix Blocked By | id |
| Estimation Technique | Residual PL |
| Degrees of Freedom Method | None |
| Fixed Effects SE Adjustment | Sandwich - Classical |
According to the compound symmetry model, there is substantial correlation among the observations from the same subject (Output 38.12.4).
The parameter estimates in Output 38.12.5 are the same as in the Poisson generalized linear model (Output 38.12.2), because of the balance in these data. The standard errors have increased substantially, however, by taking into account the correlations among the observations.
Copyright © SAS Institute, Inc. All Rights Reserved.