| The SEQDESIGN Procedure |
Example 77.1 Creating Fixed-Sample Designs
This example demonstrates a one-sided fixed-sample design and a two-sided fixed-sample design. The following statements request a fixed-sample design with an upper alternative:
ods graphics on;
proc seqdesign pss
;
OneSidedFixedSample: design nstages=1
alt=upper
alpha=0.025 beta=0.10
;
samplesize model=onesamplemean(mean=0.25);
run;
ods graphics off;
In the DESIGN statement, the label OneSidedFixedSample identifies the design in the output tables. The NSTAGES=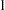 option specifies that the design has only one stage; this corresponds to a fixed-sample design. In the SEQDESIGN procedure, the null hypothesis for the design is
option specifies that the design has only one stage; this corresponds to a fixed-sample design. In the SEQDESIGN procedure, the null hypothesis for the design is 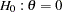 and the ALT=UPPER option specifies an upper alternative hypothesis
and the ALT=UPPER option specifies an upper alternative hypothesis  . The MEAN=
. The MEAN= option in the SAMPLESIZE statement specifies the upper alternative reference
option in the SAMPLESIZE statement specifies the upper alternative reference  .
.
The options ALPHA=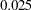 and BETA=
and BETA= specify the Type I error probability level
specify the Type I error probability level  and the Type II error probability level
and the Type II error probability level  . That is, the design has a power
. That is, the design has a power 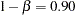 at
at  .
.
The "Design Information" table in Output 77.1.1 displays design specifications and the derived statistics such as power. As expected, the derived statistics such as maximum information and average sample number (in percentage of its corresponding fixed-sample information) are 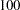 for the fixed-sample design (NSTAGES=1). Also, for a fixed-sample design, the STOP= and METHOD= options in the DESIGN statement are not applicable.
for the fixed-sample design (NSTAGES=1). Also, for a fixed-sample design, the STOP= and METHOD= options in the DESIGN statement are not applicable.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Standardized Z |
| Alternative Hypothesis | Upper |
| Alternative Reference | 0.25 |
| Number of Stages | 1 |
| Alpha | 0.025 |
| Beta | 0.1 |
| Power | 0.9 |
| Max Information (Percent of Fixed Sample) | 100 |
| Max Information | 168.1188 |
| Null Ref ASN (Percent of Fixed Sample) | 100 |
| Alt Ref ASN (Percent of Fixed Sample) | 100 |
The "Method Information" table in Output 77.1.2 displays the  and
and 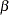 error levels. It also displays the derived drift parameter, which is the standardized reference improvement,
error levels. It also displays the derived drift parameter, which is the standardized reference improvement,  , where
, where 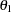 is the alternative reference and
is the alternative reference and 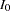 is the maximum information for the design. If either
is the maximum information for the design. If either 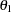 or
or 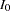 is specified, the other statistic is derived in the SEQDESIGN procedure. For a fixed-sample design,
is specified, the other statistic is derived in the SEQDESIGN procedure. For a fixed-sample design,
 |
The "Boundary Information" table in Output 77.1.3 displays information level, alternative reference, and boundary value at each stage. The information proportion indicates the proportion of maximum information available at the stage. With only one stage for a fixed-sample design, the proportion is 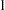 . With the SAMPLESIZE statement, the required sample size
. With the SAMPLESIZE statement, the required sample size 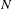 is also displayed under the heading "Information Level."
is also displayed under the heading "Information Level."
With the default BOUNDARYSCALE=STDZ option, output alternative references and boundaries are displayed with the standardized normal  scale. The alternative reference on the standardized
scale. The alternative reference on the standardized  scale at stage
scale at stage 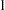 is given by
is given by  , where
, where  is the information level at stage
is the information level at stage 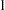 . With a boundary value
. With a boundary value 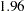 , the hypothesis of
, the hypothesis of  is rejected if the standardized normal statistic
is rejected if the standardized normal statistic  .
.
If the ODS GRAPHICS ON statement is specified, a detailed boundary plot with the rejection and acceptance regions is displayed by default, as shown in Output 77.1.4. The boundary values in the "Boundary Information" table in Figure 77.1.3 are displayed in the plot.

The "Sample Size Summary" table in Output 77.1.5 displays parameters for the sample size computation of the test for a normal mean.
The "Sample Sizes (N)" table in Output 77.1.6 displays the derived sample sizes, in both fractional and integer numbers. With the resulting integer sample sizes, the corresponding information level is slightly larger than the level from the design. This can increase the power slightly if the integer sample size is used in the trial.
The following statements request a two-sided fixed-sample design with a specified alternative reference:
ods graphics on;
proc seqdesign altref=1.2
pss
;
TwoSidedFixedSample: design nstages=1
alt=twosided
alpha=0.05 beta=0.10
;
samplesize model=twosamplemean(stddev=2 weight=2);
run;
ods graphics off;
In the SEQDESIGN procedure, the null hypothesis for the design is 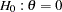 . The ALT=TWOSIDED option specifies a two-sided alternative hypothesis
. The ALT=TWOSIDED option specifies a two-sided alternative hypothesis  . The ALTREF=1.2 option in the PROC SEQDESIGN statement specifies the alternative reference
. The ALTREF=1.2 option in the PROC SEQDESIGN statement specifies the alternative reference  .
.
The ALPHA=0.05 option specifies the two-sided Type I error probability level 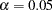 . That is, the lower and upper Type I error probabilities
. That is, the lower and upper Type I error probabilities  . The BETA=0.10 option specifies the Type II error probability level
. The BETA=0.10 option specifies the Type II error probability level  , and the design has a power
, and the design has a power 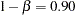 at the alternative reference
at the alternative reference  .
.
The "Design Information" table in Output 77.1.7 displays design specifications and the derived power. With a specified alternative reference, the maximum information is derived.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Standardized Z |
| Alternative Hypothesis | Two-Sided |
| Alternative Reference | 1.2 |
| Number of Stages | 1 |
| Alpha | 0.05 |
| Beta | 0.1 |
| Power | 0.9 |
| Max Information (Percent of Fixed Sample) | 100 |
| Max Information | 7.296822 |
| Null Ref ASN (Percent of Fixed Sample) | 100 |
| Alt Ref ASN (Percent of Fixed Sample) | 100 |
The "Method Information" table in Output 77.1.8 displays the  and
and 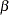 errors, alternative references, and drift parameter. For a fixed-sample design, the derived drift parameter
errors, alternative references, and drift parameter. For a fixed-sample design, the derived drift parameter
 |
With a specified alternative reference  , the maximum information
, the maximum information
 |
The default "Boundary Information" table in Output 77.1.9 displays information level, alternative reference, and boundary values. With the default BOUNDARYSCALE=STDZ option, alternative reference and boundary values are displayed with the standardized normal  scale. Thus, the standardized alternative references
scale. Thus, the standardized alternative references  are displayed.
are displayed.
With boundary values of 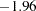 and
and 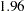 , the hypothesis of
, the hypothesis of  is rejected if the standardized normal statistic
is rejected if the standardized normal statistic  or
or  .
.
With the specified ODS GRAPHICS ON statement, a detailed boundary plot with the rejection and acceptance regions is displayed by default, as shown in Output 77.1.10 . The boundary values in the "Boundary Information" table in Figure 77.1.9 are displayed in the plot.

The "Sample Size Summary" table in Output 77.1.11 displays parameters for the sample size computation of the test for a normal mean.
The "Sample Sizes (N)" table in Output 77.1.12 displays the derived sample sizes, in both fractional and integer numbers. With the WEIGHT= option, the allocation ratio is
option, the allocation ratio is  for the first group and
for the first group and 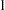 for the second group. With the resulting integer sample sizes, the corresponding information level is slightly larger than the level from the design. This can increase the power slightly if the integer sample size is used in the trial.
for the second group. With the resulting integer sample sizes, the corresponding information level is slightly larger than the level from the design. This can increase the power slightly if the integer sample size is used in the trial.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.