PROC CANCORR: Canonical Correlation Analysis of Fitness Club Data :: SAS/STAT(R) 9.2 User's Guide, Second Edition

The CANCORR Procedure

Example 26.1 Canonical Correlation Analysis of Fitness Club Data

Three physiological and three exercise variables are measured on 20 middle-aged men in a fitness club. You can use the CANCORR procedure to determine whether the physiological variables are related in any way to the exercise variables. The following statements create the SAS data set Fit and produce Output 26.1.1 through Output 26.1.5:

   data Fit;
      input Weight Waist Pulse Chins Situps Jumps;
      datalines;
   191  36  50   5  162   60
   189  37  52   2  110   60
   193  38  58  12  101  101
   162  35  62  12  105   37
   189  35  46  13  155   58
   182  36  56   4  101   42
   211  38  56   8  101   38
   167  34  60   6  125   40
   176  31  74  15  200   40
   154  33  56  17  251  250
   169  34  50  17  120   38
   166  33  52  13  210  115
   154  34  64  14  215  105
   247  46  50   1   50   50
   193  36  46   6   70   31
   202  37  62  12  210  120
   176  37  54   4   60   25
   157  32  52  11  230   80
   156  33  54  15  225   73
   138  33  68   2  110   43
   ;

   proc cancorr data=Fit all
        vprefix=Physiological vname='Physiological Measurements'
        wprefix=Exercises wname='Exercises';
      var Weight Waist Pulse;
      with Chins Situps Jumps;
      title 'Middle-Aged Men in a Health Fitness Club';
      title2 'Data Courtesy of Dr. A. C. Linnerud, NC State Univ';
   run;

Output 26.1.1 Correlations among the Original Variables

Middle-Aged Men in a Health Fitness Club

Data Courtesy of Dr. A. C. Linnerud, NC State Univ

The CANCORR Procedure

Correlations Among the Original Variables

Correlations Among the Physiological Measurements
	Weight	Waist	Pulse
Weight	1.0000	0.8702	-0.3658
Waist	0.8702	1.0000	-0.3529
Pulse	-0.3658	-0.3529	1.0000

Correlations Among the Exercises
	Chins	Situps	Jumps
Chins	1.0000	0.6957	0.4958
Situps	0.6957	1.0000	0.6692
Jumps	0.4958	0.6692	1.0000

Correlations Between the Physiological Measurements and the Exercises
	Chins	Situps	Jumps
Weight	-0.3897	-0.4931	-0.2263
Waist	-0.5522	-0.6456	-0.1915
Pulse	0.1506	0.2250	0.0349

Output 26.1.1 displays the correlations among the original variables. The correlations between the physiological and exercise variables are moderate, the largest being 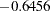$\text{[math]}$ between Waist and Situps. There are larger within-set correlations: 0.8702 between Weight and Waist, 0.6957 between Chins and Situps, and 0.6692 between Situps and Jumps.

Output 26.1.2 Canonical Correlations and Multivariate Statistics

Middle-Aged Men in a Health Fitness Club

Data Courtesy of Dr. A. C. Linnerud, NC State Univ

The CANCORR Procedure

Canonical Correlation Analysis

	Canonical Correlation	Adjusted Canonical Correlation	Approximate Standard Error	Squared Canonical Correlation	Eigenvalues of Inv(E)*H = CanRsq/(1-CanRsq)				Test of H0: The canonical correlations in the current row and all that follow are zero
	Canonical Correlation	Adjusted Canonical Correlation	Approximate Standard Error	Squared Canonical Correlation	Eigenvalue	Difference	Proportion	Cumulative	Likelihood Ratio	Approximate F Value	Num DF	Den DF	Pr > F
1	0.795608	0.754056	0.084197	0.632992	1.7247	1.6828	0.9734	0.9734	0.35039053	2.05	9	34.223	0.0635
2	0.200556	-.076399	0.220188	0.040223	0.0419	0.0366	0.0237	0.9970	0.95472266	0.18	4	30	0.9491
3	0.072570	.	0.228208	0.005266	0.0053		0.0030	1.0000	0.99473355	0.08	1	16	0.7748

Multivariate Statistics and F Approximations
S=3 M=-0.5 N=6
Statistic	Value	F Value	Num DF	Den DF	Pr > F
Wilks' Lambda	0.35039053	2.05	9	34.223	0.0635
Pillai's Trace	0.67848151	1.56	9	48	0.1551
Hotelling-Lawley Trace	1.77194146	2.64	9	19.053	0.0357
Roy's Greatest Root	1.72473874	9.20	3	16	0.0009
NOTE: F Statistic for Roy's Greatest Root is an upper bound.

As Output 26.1.2 shows, the first canonical correlation is 0.7956, which would appear to be substantially larger than any of the between-set correlations. The probability level for the null hypothesis that all the canonical correlations are zero in the population is only 0.0635, so no firm conclusions can be drawn. The remaining canonical correlations are not worthy of consideration, as can be seen from the probability levels and especially from the negative adjusted canonical correlations.

Because the variables are not measured in the same units, the standardized coefficients rather than the raw coefficients should be interpreted. The correlations given in the canonical structure matrices should also be examined.

Output 26.1.3 Raw and Standardized Canonical Coefficients

Raw Canonical Coefficients for the Physiological Measurements
	Physiological1	Physiological2	Physiological3
Weight	-0.031404688	-0.076319506	-0.007735047
Waist	0.4932416756	0.3687229894	0.1580336471
Pulse	-0.008199315	-0.032051994	0.1457322421

Raw Canonical Coefficients for the Exercises
	Exercises1	Exercises2	Exercises3
Chins	-0.066113986	-0.071041211	-0.245275347
Situps	-0.016846231	0.0019737454	0.0197676373
Jumps	0.0139715689	0.0207141063	-0.008167472

Standardized Canonical Coefficients for the Physiological Measurements
	Physiological1	Physiological2	Physiological3
Weight	-0.7754	-1.8844	-0.1910
Waist	1.5793	1.1806	0.5060
Pulse	-0.0591	-0.2311	1.0508

Standardized Canonical Coefficients for the Exercises
	Exercises1	Exercises2	Exercises3
Chins	-0.3495	-0.3755	-1.2966
Situps	-1.0540	0.1235	1.2368
Jumps	0.7164	1.0622	-0.4188

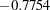The first canonical variable for the physiological variables, displayed in Output 26.1.3, is a weighted difference of Waist (1.5793) and Weight ( $\text{[math]}$ ), with more emphasis on Waist. The coefficient for Pulse is near 0. The correlations between Waist and Weight and the first canonical variable are both positive, 0.9254 for Waist and 0.6206 for Weight. Weight is therefore a suppressor variable, meaning that its coefficient and its correlation have opposite signs.

The first canonical variable for the exercise variables also shows a mixture of signs, subtracting Situps (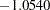 $\text{[math]}$ ) and Chins ( 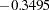$\text{[math]}$ ) from Jumps (0.7164), with the most weight on Situps. All the correlations are negative, indicating that Jumps is also a suppressor variable.

It might seem contradictory that a variable should have a coefficient of opposite sign from that of its correlation with the canonical variable. In order to understand how this can happen, consider a simplified situation: predicting Situps from Waist and Weight by multiple regression. In informal terms, it seems plausible that obese people should do fewer sit-ups than skinny people. Assume that the men in the sample do not vary much in height, so there is a strong correlation between Waist and Weight (0.8702). Examine the relationships between obesity and the independent variables:

People with large waists tend to be more obese than people with small waists. Hence, the correlation between Waist and Situps should be negative.
People with high weights tend to be more obese than people with low weights. Therefore, Weight should correlate negatively with Situps.
For a fixed value of Weight, people with large waists tend to be shorter and more obese. Thus, the multiple regression coefficient for Waist should be negative.
For a fixed value of Waist, people with higher weights tend to be taller and skinnier. The multiple regression coefficient for Weight should therefore be positive, of opposite sign from the correlation between Weight and Situps.

Therefore, the general interpretation of the first canonical correlation is that Weight and Jumps act as suppressor variables to enhance the correlation between Waist and Situps. This canonical correlation might be strong enough to be of practical interest, but the sample size is not large enough to draw definite conclusions.

The canonical redundancy analysis (Output 26.1.4) shows that neither of the first pair of canonical variables is a good overall predictor of the opposite set of variables, the proportions of variance explained being 0.2854 and 0.2584. The second and third canonical variables add virtually nothing, with cumulative proportions for all three canonical variables being 0.2969 and 0.2767.

Output 26.1.4 Canonical Redundancy Analysis

Middle-Aged Men in a Health Fitness Club

Data Courtesy of Dr. A. C. Linnerud, NC State Univ

The CANCORR Procedure

Canonical Redundancy Analysis

Standardized Variance of the Physiological Measurements Explained by
Canonical Variable Number	Their Own Canonical Variables		Canonical R-Square	The Opposite Canonical Variables
Canonical Variable Number	Proportion	Cumulative Proportion	Canonical R-Square	Proportion	Cumulative Proportion
1	0.4508	0.4508	0.6330	0.2854	0.2854
2	0.2470	0.6978	0.0402	0.0099	0.2953
3	0.3022	1.0000	0.0053	0.0016	0.2969

Standardized Variance of the Exercises Explained by
Canonical Variable Number	Their Own Canonical Variables		Canonical R-Square	The Opposite Canonical Variables
Canonical Variable Number	Proportion	Cumulative Proportion	Canonical R-Square	Proportion	Cumulative Proportion
1	0.4081	0.4081	0.6330	0.2584	0.2584
2	0.4345	0.8426	0.0402	0.0175	0.2758
3	0.1574	1.0000	0.0053	0.0008	0.2767

The squared multiple correlations (Output 26.1.5) indicate that the first canonical variable of the physiological measurements has some predictive power for Chins (0.3351) and Situps (0.4233) but almost none for Jumps (0.0167). The first canonical variable of the exercises is a fairly good predictor of Waist (0.5421), a poorer predictor of Weight (0.2438), and nearly useless for predicting Pulse (0.0701).

Output 26.1.5 Canonical Redundancy Analysis

Squared Multiple Correlations Between the Physiological Measurements and the First M Canonical Variables of the Exercises
M	1	2	3
Weight	0.2438	0.2678	0.2679
Waist	0.5421	0.5478	0.5478
Pulse	0.0701	0.0702	0.0749

Squared Multiple Correlations Between the Exercises and the First M Canonical Variables of the Physiological Measurements
M	1	2	3
Chins	0.3351	0.3374	0.3396
Situps	0.4233	0.4365	0.4365
Jumps	0.0167	0.0536	0.0539

Top of Page