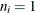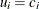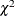CCHART Statement: SHEWHART Procedure

Constructing Charts for Numbers of Nonconformities (c Charts)

The following notation is used in this section:

u	expected number of nonconformities per unit produced by the process
$u_{i}$	number of nonconformities per unit in the ith subgroup
$c_{i}$	total number of nonconformities in the ith subgroup
$n_{i}$	number of inspection units in the ith subgroup. Typically, $n_{i} = 1$ and $u_ i=c_ i$ for c charts. In general, $u_{i}=c_{i}/n_{i}$ .
$\bar{u}$	average number of nonconformities per unit taken across subgroups. The quantity $\bar{u}$ is computed as a weighted average: $\bar{u} = \frac{n_{1}u_{1} + \cdots + n_{N}u_{N}}{n_{1} + \cdots + n_{N}} = \frac{c_{1} + \cdots + c_{N}}{n_{1} + \cdots + n_{N}}$
N	number of subgroups
$\chi ^{2}_{\nu }$	has a central $\chi ^{2}$ distribution with $\nu$ degrees of freedom

Plotted Points

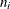Each point on a c chart represents the total number of nonconformities ( $c_{i}$ ) in a subgroup. For example, Figure 18.24 displays three sections of pipeline that are inspected for defective welds (indicated by an X). Each section represents a subgroup composed of a number of inspection units, which are 1000-foot-long sections. The number of units in the ith subgroup is denoted by $n_{i}$ , which is the subgroup sample size. The value of 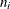$n_{i}$ can be fractional; Figure 18.24 shows 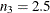$n_{3}=2.5$ units in the third subgroup.

Figure 18.24: Terminology for c Charts and u Charts

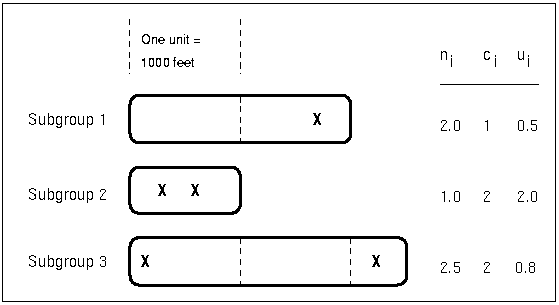
The number of nonconformities in the ith subgroup is denoted by $c_{i}$ . The number of nonconformities per unit in the ith subgroup is denoted by $u_{i}=c_{i}/n_{i}$ . In Figure 18.24, the number of welds per inspection unit in the third subgroup is $u_{3}=2/2.5=0.8$ .

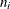A u chart created with the UCHART statement plots the quantity $u_{i}$ for the ith subgroup (see UCHART Statement: SHEWHART Procedure). An advantage of a u chart is that the value of the central line at the ith subgroup does not depend on $n_{i}$ . This is not the case for a c chart, and consequently, a u chart is often preferred when the number of units 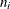$n_{i}$ is not constant across subgroups.

Central Line

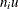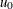On a c chart, the central line indicates an estimate for $n_{i}u$ , which is computed as $n_{i}\bar{u}$ . If you specify a known value ( $u_{0}$ ) for u, the central line indicates the value of $n_{i}u_{0}$ .

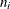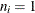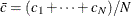Note that the central line varies with subgroup sample size $n_{i}$ . When $n_{i}=1$ for all subgroups, the central line has the constant value $\bar{c} = (c_{1} + \cdots + c_{N})/N$ .

Control Limits

You can compute the limits in the following ways:

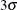as a specified multiple (k) of the standard error of $c_{i}$ above and below the central line. The default limits are computed with k = 3 (these are referred to as $3\sigma$ limits).
as probability limits defined in terms of $\alpha$ , a specified probability that $c_{i}$ exceeds the limits

The lower and upper control limits, LCLC and UCLC respectively, are given by

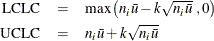
$\begin{eqnarray*} \mbox{LCLC} & = & \mbox{max}\left(n_{i}\bar{u} - k\sqrt {n_{i}\bar{u}}\; ,0 \right) \\ \mbox{UCLC} & = & n_{i}\bar{u}+ k\sqrt {n_{i}\bar{u}} \end{eqnarray*}$

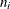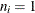The upper and lower control limits vary with the number of inspection units per subgroup $n_{i}$ . If $n_ i=1$ for all subgroups, the control limits have constant values.

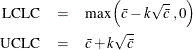
$\begin{eqnarray*} \mbox{LCLC} & = & \mbox{max}\left(\bar{c} - k\sqrt {\bar{c}}\; ,0 \right) \\ \mbox{UCLC} & = & \bar{c}+ k\sqrt {\bar{c}} \end{eqnarray*}$

An upper probability limit UCLC for $c_{i}$ can be determined using the fact that

$\begin{array}{ll} P\{ c_{i} > \mbox{UCLC}\} & = 1 - P\{ c_{i} \leq \mbox{UCLC} \} \\ & = 1 - P\{ \chi ^{2}_{2(\! {\scriptstyle \text {UCLC}}+1)} \geq 2n_{i}\bar{u}\} \end{array}$

The upper probability limit UCLC is then calculated by setting

$1 - P\{ \chi ^{2}_{2(\! {\scriptstyle \text {UCLC}}+1)} \geq 2n_{i}\bar{u}\} = \alpha /2$

and solving for UCLC.

A similar approach is used to calculate the lower probability limit LCLC, using the fact that

$\begin{array}{ll} P\{ c_{i} < \mbox{LCLC}\} & = P\{ c_{i} \leq \mbox{LCLC}-1\} \\ & = P\{ \chi ^{2}_{2(\! {(\scriptstyle \text {LCLC}}-1)+1)} > 2n_{i}\bar{u}\} \\ & = P\{ \chi ^{2}_{2\scriptstyle \text {LCLC}} > 2n_{i}\bar{u}\} \end{array}$

The lower probability limit LCLC is then calculated by setting

$P\{ \chi ^{2}_{2\scriptstyle \text {LCLC}} > 2n_{i}\bar{u}\} = \alpha /2$

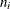and solving for LCLC. This assumes that the process is in statistical control and that $c_{i}$ has a Poisson distribution. For more information, refer to Johnson, Kotz, and Kemp (1992). Note that the probability limits vary with the number of inspection units per subgroup ( $n_ i$ ) and are asymmetric about the central line.

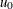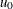If a standard value $u_{0}$ is available for u, replace $\bar{u}$ with $u_0$ in the formulas for the control limits. You can specify parameters for the limits as follows:

Specify k with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
Specify $\alpha$ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
Specify a constant nominal sample size 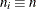$n_{i} \equiv n$ for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
Specify 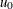$u_{0}$ with the U0= option or with the variable _U_ in a LIMITS= data set.