PROC SHEWHART: Diagnosing and Modeling Autocorrelation

The SHEWHART Procedure

Diagnosing and Modeling Autocorrelation

You can diagnose autocorrelation with an autocorrelation plot created with the ARIMA procedure.

title ;
proc arima data=Chemical;
   identify var = xt;
run;

Refer to SAS/ETS 9.22 User's Guide for details on the ARIMA procedure. The plot, shown in Figure 13.43.75, indicates that the data are highly autocorrelated with a lag 1 autocorrelation of 0.83.

Output 13.43.75 Autocorrelation Plots for Chemical Data

The ARIMA Procedure

Autocorrelations
Lag	Covariance	Correlation	Std Error
0	48.348400	1.00000	0
1	40.141884	0.83026	0.100000
2	34.732168	0.71837	0.154229
3	29.950852	0.61948	0.184683
4	24.739536	0.51169	0.204409
5	20.594420	0.42596	0.216840
6	18.427704	0.38114	0.225052
7	17.400188	0.35989	0.231417
8	17.621272	0.36446	0.236948
9	18.363756	0.37982	0.242489
10	16.754040	0.34653	0.248367
11	16.844924	0.34841	0.253156
12	17.137208	0.35445	0.257906
13	16.884092	0.34922	0.262732
14	17.927976	0.37081	0.267334
15	16.801860	0.34752	0.272429
16	17.076544	0.35320	0.276826
17	17.815028	0.36847	0.281296
18	16.501312	0.34130	0.286082
19	14.662196	0.30326	0.290126
20	12.612280	0.26086	0.293278
21	11.105364	0.22969	0.295590
22	8.891648	0.18391	0.297369
23	6.794132	0.14052	0.298504
24	4.732816	0.09789	0.299165

"." marks two standard errors

Partial Autocorrelations
Lag	Correlation
1	0.83026
2	0.09346
3	0.00385
4	-0.07340
5	-0.00278
6	0.09013
7	0.08781
8	0.10327
9	0.07240
10	-0.11637
11	0.08210
12	0.07580
13	0.04429
14	0.11661
15	-0.10446
16	0.07703
17	0.07376
18	-0.07080
19	-0.02814
20	-0.08559
21	0.01962
22	-0.04599
23	-0.07878
24	-0.02303

The partial autocorrelation plot in Figure 13.43.75 suggests that the data can be modeled with a first-order autoregressive model, commonly referred to as an AR(1) model.

$\text{[math]}$

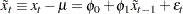You can fit this model with the ARIMA procedure. The results in Figure 13.43.76 show that the equation of the fitted model is 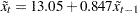$\text{[math]}$ .

proc arima data=Chemical;
   identify var=xt;
   estimate p=1 method=ml;
run;

Output 13.43.76 Fitted AR(1) Model

The ARIMA Procedure

Maximum Likelihood Estimation
Parameter	Estimate	Standard Error	t Value	Approx Pr > \|t\|	Lag
MU	85.28375	2.32973	36.61	<.0001	0
AR1,1	0.84694	0.05221	16.22	<.0001	1

Constant Estimate	13.05329
Variance Estimate	14.27676
Std Error Estimate	3.77846
AIC	552.8942
SBC	558.1045
Number of Residuals	100

Top of Page