The OPTMODEL Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Named ParametersIndexingTypesNamesParametersExpressionsIdentifier ExpressionsFunction ExpressionsIndex SetsOPTMODEL Expression ExtensionsConditions of OptimalityData Set Input/OutputControl FlowFormatted OutputODS Table and Variable NamesConstraintsSuffixesInteger Variable SuffixesDual ValuesReduced CostsPresolverModel UpdateMultiple SubproblemsMultiple SolutionsProblem SymbolsOPTMODEL OptionsAutomatic DifferentiationConversionsFCMP RoutinesMore on Index SetsThreaded and Distributed ProcessingMacro Variable _OROPTMODEL_Rewriting PROC NLP Models for PROC OPTMODEL
Named ParametersIndexingTypesNamesParametersExpressionsIdentifier ExpressionsFunction ExpressionsIndex SetsOPTMODEL Expression ExtensionsConditions of OptimalityData Set Input/OutputControl FlowFormatted OutputODS Table and Variable NamesConstraintsSuffixesInteger Variable SuffixesDual ValuesReduced CostsPresolverModel UpdateMultiple SubproblemsMultiple SolutionsProblem SymbolsOPTMODEL OptionsAutomatic DifferentiationConversionsFCMP RoutinesMore on Index SetsThreaded and Distributed ProcessingMacro Variable _OROPTMODEL_Rewriting PROC NLP Models for PROC OPTMODEL -
Examples

- References
Programming Statements
- Assignment Statement
- CALL Statement
- CLOSEFILE Statement
- COFOR Statement
- CONTINUE Statement
- CREATE DATA Statement
- DO Statement
- DO Statement, Iterative
- DO UNTIL Statement
- DO WHILE Statement
- DROP Statement
- EXPAND Statement
- FILE Statement
- FIX Statement
- FOR Statement
- IF Statement
- LEAVE Statement
- Null Statement
- PERFORMANCE Statement
- PRINT Statement
- PROFILE Statement
- PUT Statement
- QUIT Statement
- READ DATA Statement
- RESET OPTIONS Statement
- RESTORE Statement
- SAVE MPS Statement
- SAVE QPS Statement
- SOLVE Statement
- STOP Statement
- SUBMIT Statement
- UNFIX Statement
- USE PROBLEM Statement
PROC OPTMODEL supports several programming statements. You can perform various actions with these statements, such as reading or writing data sets, setting parameter values, generating text output, or invoking a solver.
Statements are read from the input and are executed immediately when complete. Certain statements can contain one or more substatements. The execution of substatements is held until the statements that contain them are submitted. Parameter values that are used by expressions in programming statements are resolved when the statement is executed; this resolution might cause errors to be detected. For example, the use of undefined parameters is detected during resolution of the symbolic expressions from declarations.
A statement is terminated by a semicolon. The positions at which semicolons are placed are shown explicitly in the following statement syntax descriptions.
The programming statements can be grouped into the categories shown in Table 5.7.
Table 5.7: Types of Programming Statements in PROC OPTMODEL
Assignment Statement
-
identifier-expression = expression;
The assignment statement assigns a variable or parameter value. The type of the target identifier-expression must match the type of the right-hand-side expression.
For example, the following statements set the current value for variable x to 3:
proc optmodel; var x; x = 3;
Note: Parameters that were declared with the equal sign (=) initialization forms must not be reassigned a value with an assignment statement. If this occurs, PROC OPTMODEL reports an error.
CALL Statement
-
CALL name ( argument-1
 , …argument-n
, …argument-n ![$\ms {]}$](images/ormpug_optmodel0027.png) );
);
The CALL statement invokes the named library subroutine. The values that are determined for each argument expression are passed
to the subroutine when the subroutine is invoked. The subroutine can update the values of PROC OPTMODEL parameters and variables
when an argument is an identifier-expression (see the section Identifier Expressions). For example, the following statements set the parameter array a to a random permutation of 1 to 4:
proc optmodel;
number a{i in 1..4} init i;
number seed init -1;
call ranperm(seed, a[1], a[2], a[3], a[4]);
Note: The maximum length of the string value returned from an output argument is equal to the character length of the argument before the call. An undefined STRING parameter that is used as an output argument has a character length of 8.
For a list of CALL routines, see SAS Functions and CALL Routines: Reference. You can also call subroutines that are compiled by the FCMP procedure. For more information, see the section FCMP Routines.
CLOSEFILE Statement
-
CLOSEFILE file-specifications;
The CLOSEFILE statement closes files that were opened by the FILE statement. Each file is specified by a logical name, a physical filename in quotation marks, or an expression enclosed in parentheses that evaluates to a physical filename. See the section FILE Statement for more information about file specifications.
The following example shows how the CLOSEFILE statement is used with a logical filename:
filename greet 'hello.txt'; proc optmodel; file greet; put 'Hi!'; closefile greet;
Generally you must close a file with a CLOSEFILE statement before external programs can access the file. However, any open files are automatically closed when PROC OPTMODEL terminates.
COFOR Statement
-
COFOR { index-set } statement;
The COFOR statement executes its statement for each member of the specified index-set , similar to how the FOR statement executes. However, in a COFOR statement, PROC OPTMODEL can execute the SOLVE statement concurrently with other statements. The execution of the COFOR substatement is interleaved between loop iterations so that other iterations can be processed while an iteration waits for a SOLVE statement to complete. Multiple solvers can run concurrently. This interleaving is managed so that in many cases a FOR loop can be replaced by a COFOR loop to achieve concurrency with minimal or no other changes to the code.
The following code shows a simple example:
proc optmodel printlevel=0;
var x {1..6} >= 0;
minimize z = sum {j in 1..6} x[j];
con a1: x[1] + x[2] + x[3] <= 4;
con a2: x[4] + x[5] + x[6] <= 6;
con a3: x[1] + x[4] >= 5;
con a4: x[2] + x[5] >= 2;
con a5: x[3] + x[6] >= 3;
cofor{i in 3..5} do;
fix x[1]=i;
solve;
put i= x[1]= _solution_status_=;
end;
Figure 5.7 shows the PROC OPTMODEL output. The order of the output from different iterations can vary between runs, depending on the order in which the SOLVE statements complete. A FOR statement could have been used instead of COFOR; the FOR statement would produce a consistent output order but only one solver would execute at a time. Note that because the solver execution in this example is trivial, the benefits from concurrency are limited.
Figure 5.7: A Simple COFOR Loop
A COFOR statement can contain other control and looping statements , including nested COFOR loops. The maximum number of threads that can be used is controlled by the PERFORMANCE statement and SAS options that are in effect when the outermost COFOR loop is entered, as described in the section Threaded and Distributed Processing. The outermost COFOR statement allocates threads for execution on the computer that is running PROC OPTMODEL. When a PERFORMANCE statement is in effect that requests distributed computing, the outermost COFOR statement also creates a distributed execution environment that has the specified number of compute nodes. Solvers within the COFOR loop can then run remotely in single-machine mode on the compute nodes (as shown in the solver output).
The COFOR statement supports simultaneous processing of several SOLVE statements. Processing proceeds through the iteration body statements as it would through a FOR loop until a SOLVE statement that uses the CLP, LP, MILP, network, NLP, or QP solver is executed. After the problem is generated, the solver starts processing in a background thread (or remote computing node in the distributed case) and the COFOR loop switches execution to another iteration of the loop, assuming enough threads and iterations are available. (Note that you need at least two threads on the computer that is running the COFOR loop to enable overlap of statement execution with solver execution.) Execution could switch to an existing iteration where the solver has completed. Alternatively, a new iteration of a COFOR loop could be started. All output from an iteration, except within a SUBMIT block, is displayed together after the iteration has completed. Output from a SUBMIT block is displayed as the block is executed.
A COFOR loop can contain PERFORMANCE statements. These statements affect SOLVE statements that are executed subsequently in the same iteration but not those in other iterations. When a COFOR statement is running in distributed mode, the default value of the NTHREADS= option in the PERFORMANCE statement is the number of threads per compute node, as determined when the outermost COFOR loop starts. Otherwise the default value of the NTHREADS= option is 1. Executing SOLVE statements in the background by using a single thread usually provides the best performance on a single computer.
Each iteration of a COFOR loop begins execution by setting default performance options. In effect, each iteration of a COFOR loop begins with an implicit PERFORMANCE statement,
performance parallelmode=<outer-mode> <details>;
where PARALLELMODE=<outer-mode> and <details> represent the PARALLELMODE= and DETAILS options, if any, in the PERFORMANCE statement in effect at the start of the COFOR loop. The NTHREADS= option is set to its default value. The following example shows how performance options are inherited:
performance nodes=10 nthreads=16
parallelmode=nondeterministic;
cofor {iter in ITERSET} do;
/* implicit statement, uses default NTHREADS=16 */
* performance parallelmode=nondeterministic;
/* set up problem */
. . .
/* runs with NTHREADS=16, nondeterministic */
solve with lp/algorithm=con;
/* change problem */
. . .
/* reset NTHREADS=, default PARALLELMODE=DETERMINISTIC */
performance nthreads=8;
/* runs with NTHREADS=8, deterministic */
solve with lp/algorithm=ip;
end;
/* the PERFORMANCE statement preceding the COFOR resumes effect */
The order in which the solvers complete is unpredictable. So it is usually not useful for a problem that is solved within an iteration to depend on the results of SOLVE statements that are executed in other iterations of the COFOR loop. It is advisable to limit global parameter updates to operations where order is not important, such as accumulating counts, sums, or unions or writing mutually exclusive subsets of an array. It is possible to execute multiple SOLVE statements within a loop iteration, and subsequent solver invocations within an iteration can use results from prior solvers in the same iteration.
In many cases, a COFOR loop iteration solves a specialized version of a common problem structure. This requires it to modify
problem attributes that are also used in other iterations, such as coefficient values or the fixed status of variables. Changes
to problem attributes are not made visible to other iterations of a COFOR loop in order to avoid confusing behavior due to
interleaved execution. For example, the value printed for x[1] in Figure 5.7 is the local value for the iteration, not the most recent global value. Changes to these attributes create or update a copy
of the value that is local to the iteration. These attribute values along with the local dummy parameters provide a local
context for the iteration.
The following problem attributes are automatically made local to the modifying iteration when they are changed within a COFOR loop:
-
the current problem, selected by USE PROBLEM
-
the value of variables and their suffix values
-
the fixed status of variables
-
the constraint suffix values
-
the dropped status of constraints
-
the .LABEL suffix
-
NUMBER, STRING, and SET parameters that determine values that are used in the bounds or body expressions of problem declarations (CONSTRAINT, IMPVAR, MIN, MAX, or VAR)
-
NUMBER, STRING, and SET parameters that determine values that are used in solver arguments within the same outermost COFOR loop
-
the predeclared string parameters _SOLVER_OPTIONS_ and _solver_OPTIONS_ (for each solver)
To illustrate these rules, consider the following code, which uses the NLP solver to solve a MINLP portfolio optimization problem by selecting random subsets of the assets to optimize:
proc optmodel printlevel=0;
/* assets and related parameters */
set ASSETS;
num return {ASSETS};
num cov {ASSETS, ASSETS} init 0;
read data means into ASSETS=[_n_] return;
read data covdata into [asset1 asset2] cov cov[asset2,asset1]=cov;
num riskLimit init 0.00025;
num minThreshold init 0.1;
num numTrials = 10;
/* number of random trials */
set TRIALS = 1..numTrials;
/* declare NLP problem for fixed set of assets */
set ASSETS_THIS;
var AssetPropVar {ASSETS} >= minThreshold <= 1;
max ExpectedReturn = sum {i in ASSETS} return[i] * AssetPropVar[i];
con RiskBound:
sum {i in ASSETS_THIS, j in ASSETS_THIS}
cov[i,j] * AssetPropVar[i] * AssetPropVar[j] <= riskLimit;
con TotalPortfolio:
sum {asset in ASSETS} AssetPropVar[asset] = 1;
/* parameters to track best solution */
num infinity = constant('BIG');
num best_objective init -infinity;
set INCUMBENT;
/* iterate over trials */
num start {TRIALS};
num finish {TRIALS};
num overall_start;
overall_start = time();
call streaminit(1);
cofor {trial in TRIALS} do;
start[trial] = time() - overall_start;
put;
put trial=;
ASSETS_THIS = {i in ASSETS: rand('UNIFORM') < 0.5};
put ASSETS_THIS=;
for {i in ASSETS diff ASSETS_THIS}
fix AssetPropVar[i] = 0;
solve with NLP / logfreq=0;
put _solution_status_=;
if _solution_status_ ne 'INFEASIBLE' then do;
if best_objective < ExpectedReturn then do;
best_objective = ExpectedReturn;
INCUMBENT = ASSETS_THIS;
end;
end;
finish[trial] = time() - overall_start;
end;
put best_objective= INCUMBENT=;
create data ganttdata from [trial] e_start=start e_finish=finish;
proc gantt data=ganttdata;
id trial;
chart / compress nolegend nojobnum mindate=0 top height=1.8;
run;
All the COFOR loop iterations use the same problem, _START_. However, the changes to the problem are local to the iteration that makes them. For example, the FIX statement does not
affect variables in other iterations. The value of the ASSETS_THIS parameter is used by the RiskBound constraint, so the change to it is local. Because AssetPropVar is a VAR, the changes to its value are also local.
On the other hand, the values of the best_objective and INCUMBENT parameters do not affect any problem declarations. Therefore, their global values are used, enabling the code in the COFOR
loop to select and save the best result. Similarly, the start and finish parameters are not used in the problem and allow the overlapping of iterations to be illustrated. Figure 5.8 from the GANTT procedure shows how the iterations have overlapped execution times.
Figure 5.8: Overlapped COFOR Iterations

Changes to problem attributes from completed iterations are made visible after the loop is finished. They appear in the context that contained the COFOR statement. If multiple iterations modify the same problem attribute value, then the value from the iteration that completed last is the one made visible.
The LEAVE statement can be used to terminate execution of a COFOR loop. This completes the current iteration of the COFOR loop. The currently active solvers for the COFOR loop are terminated, and the output of the incomplete iterations is discarded. The CONTINUE statement within a COFOR loop can also be used to complete the current iteration, but it has no effect on other iterations.
Using the LEAVE statement to terminate is useful, for example, when a sufficiently good solution is found for a problem. The preceding code has been modified as follows to keep generating solutions until a time limit is reached. The code sets a time limit and then executes the LEAVE statement to stop processing when the limit is exceeded. The COFOR loop uses a very large iteration range to allow it to run indefinitely.
proc optmodel printlevel=0;
set ASSETS;
num return {ASSETS};
num cov {ASSETS, ASSETS} init 0;
read data means into ASSETS=[_n_] return;
read data covdata into [asset1 asset2] cov cov[asset2,asset1]=cov;
num riskLimit init 0.00025;
num minThreshold init 0.1;
/* declare NLP problem for fixed set of assets */
set ASSETS_THIS;
var AssetPropVar {ASSETS} >= minThreshold <= 1;
max ExpectedReturn = sum {i in ASSETS} return[i] * AssetPropVar[i];
con RiskBound:
sum {i in ASSETS_THIS, j in ASSETS_THIS}
cov[i,j] * AssetPropVar[i] * AssetPropVar[j] <= riskLimit;
con TotalPortfolio:
sum {asset in ASSETS} AssetPropVar[asset] = 1;
num infinity = constant('BIG');
num best_objective init -infinity;
set INCUMBENT;
/* run for 30 seconds */
num last_time;
last_time = time() + 30;
num n_trials init 0;
call streaminit(1);
cofor {trial in 1..1e9} do;
put;
put trial=;
ASSETS_THIS = {i in ASSETS: rand('UNIFORM') < 0.5};
put ASSETS_THIS=;
for {i in ASSETS diff ASSETS_THIS} fix AssetPropVar[i] = 0;
solve with NLP / logfreq=0;
put _solution_status_=;
if _solution_status_ ne 'INFEASIBLE' then do;
if best_objective < ExpectedReturn then do;
best_objective = ExpectedReturn;
INCUMBENT = ASSETS_THIS;
end;
end;
n_trials = n_trials + 1;
if time() >= last_time then leave;
end;
put n_trials=;
put best_objective= INCUMBENT=;
quit;
CONTINUE Statement
-
CONTINUE ;
The CONTINUE statement terminates the current iteration of the loop statement (iterative DO , DO UNTIL , DO WHILE , FOR , or COFOR ) that immediately contains the CONTINUE statement. Execution resumes at the start of the loop after checking WHILE or UNTIL tests. The FOR, COFOR, or iterative DO loops apply new iteration values.
CREATE DATA Statement
-
CREATE DATA SAS-data-set FROM
 [ key-columns ]
[ key-columns ]  = key-set
= key-set ![$\ms {]}$](images/ormpug_optmodel0027.png)
![$\ms {]}$](images/ormpug_optmodel0027.png) columns;
columns;
The CREATE DATA statement creates a new SAS data set and copies data into it from PROC OPTMODEL parameters and variables. The CREATE DATA statement can create a data set with a single observation or a data set with observations for every location in one or more arrays. The data set is closed after the execution of the CREATE DATA statement.
The arguments to the CREATE DATA statement are as follows:
- SAS-data-set
-
specifies the output data set name and options. You can specify the data set name and options directly or as the string value of an expression enclosed in parentheses. - key-columns
-
declares index values and their corresponding data set variables. The values are used to index array locations in columns. - key-set
-
specifies a set of index values for the key-columns. - columns
-
specifies data set variables as well as the PROC OPTMODEL source data for the variables.
Each column or key-column defines output data set variables and a data source for a column. For example, the following statement generates the output
SAS data set resdata from the PROC OPTMODEL array opt, which is indexed by the set indset:
create data resdata from [solns]=indset opt;
The output data set variable solns contains the index elements in indset.
Columns
Columns can have the following forms:
- identifier-expression
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
transfers data from the PROC OPTMODEL parameter or variable specified by the identifier-expression . The output data set variable has the same name as the name part of the identifier-expression (see the section Identifier Expressions). If the identifier-expression refers to an array, then the index can be omitted when it matches the key-columns. The options enable formats and labels to be associated with the data set variable. See the section Column Options for more information. The following example creates a data set with the variablesmandn:proc optmodel; number m = 7, n = 5; create data example from m n;
- name = expression
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
transfers the value of a PROC OPTMODEL expression to the output data set variable name. The expression is reevaluated for each observation. If the expression contains any operators or function calls, then it must be enclosed in parentheses. If the expression is an identifier-expression that refers to an array, then the index can be omitted if it matches the key-columns. The options enable formats and labels to be associated with the data set variable. See the section Column Options for more information. The following example creates a data set with the variableratio:proc optmodel; number m = 7, n = 5; create data example from ratio=(m/n);
- COL(name-expression) = expression
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
transfers the value of a PROC OPTMODEL expression to the output data set variable named by the string expression name-expression. The PROC OPTMODEL expression is reevaluated for each observation. If this expression contains any operators or function calls, then it must be enclosed in parentheses. If the PROC OPTMODEL expression is an identifier-expression that refers to an array, then the index can be omitted if it matches the key-columns. The options enable formats and labels to be associated with the data set variable. See the section Column Options for more information. The following example uses the COL expression to form the variables5:proc optmodel; number m = 7, n = 5; create data example from col("s"||n)=(m+n); - { index-set } < columns >
-
performs the transfers by iterating each column specified by < columns > for each member of the index set . If there are n columns and m index set members, then columns are generated. The dummy parameters from the index set can be used in the columns to generate distinct output data
set variable names in the iterated columns, using COL expressions. The columns are expanded when the CREATE DATA statement
is executed, before any output is performed. This form of columns cannot be nested. In other words, the following form of columns is NOT allowed:
columns are generated. The dummy parameters from the index set can be used in the columns to generate distinct output data
set variable names in the iterated columns, using COL expressions. The columns are expanded when the CREATE DATA statement
is executed, before any output is performed. This form of columns cannot be nested. In other words, the following form of columns is NOT allowed:
{ index-set } < { index-set } < columns > >
The following example demonstrates the use of the iterated columns form:
proc optmodel; set<string> alph = {'a', 'b', 'c'}; var x{1..3, alph} init 2; create data example from [i]=(1..3) {j in alph}<col("x"||j)=x[i,j]>;The data set created by these statements is shown in Figure 5.9.
Note: When no key-columns are specified, the output data set has a single observation.
The following statements incorporate several of the preceding examples to create and print a data set by using PROC OPTMODEL parameters:
proc optmodel;
number m = 7, n = 5;
create data example from m n ratio=(m/n) col("s"||n)=(m+n);
proc print;
run;
The output from the PRINT procedure is shown in Figure 5.10.
Column Options
Each column or key-column that defines a data set variable can be followed by zero or more of the following modifiers:
- FORMAT=format.
-
associates a format with the current column. - INFORMAT=informat.
-
associates an informat with the current column. - LABEL=’label’
-
associates a label with the current column. The label can be specified by a quoted string or an expression in parentheses. - LENGTH=length
-
specifies a length for the current column. The length can be specified by a numeric constant or a parenthesized expression. The range for character variables is 1 to 32,767 bytes. The range for numeric variables depends on the operating environment and has a minimum of 2 or 3. - TRANSCODE=YES
 NO
NO -
specifies whether character variables can be transcoded. The default value is YES. See the TRANSCODE=option of the ATTRIB statement in SAS Statements: Reference for more information.
The following statements demonstrate the use of column options, including the use of multiple options for a single column:
proc optmodel;
num sq{i in 1..10} = i*i;
create data squares from [i/format=hex2./length=3] sq/format=6.2;
proc print;
run;
The output from the PRINT procedure is shown in Figure 5.11.
Figure 5.11: CREATE DATA with Column Options
Key Columns
Key-columns declare index values that enable multiple observations to be written from array columns. An observation is created for each unique index value combination. The index values supply the index for array columns that do not have an explicit index.
Key-columns define the data set variables where the index value elements are written. They can also declare local dummy parameters for use in expressions in the columns. Key-columns are syntactically similar to columns, but are more restricted in form. The following forms of key-columns are allowed:
- name
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
transfers an index element value to the data set variable name. A local dummy parameter, name, is declared to hold the index element value. The options enable formats and labels to be associated with the data set variable. See the section Column Options for more information. - COL(name-expression)
 = index-name
= index-name ![$\ms {]}$](images/ormpug_optmodel0027.png)
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
transfers an index element value to the data set variable named by the string-valued name-expression. The argument index-name optionally declares a local dummy parameter to hold the index element value. The options enable formats and labels to be associated with the data set variable. See the section Column Options for more information.
A key-set in the CREATE DATA statement explicitly specifies the set of index values. key-set can be specified as a set expression, although it must be enclosed in parentheses if it contains any function calls or operators.
key-set can also be specified as an index set expression
, in which case the index-set dummy parameters override any dummy parameters that are declared in the key-columns items. The following statements create a data set from the PROC OPTMODEL parameter m, a matrix whose only nonzero entries are located at (1, 1) and (4, 1):
proc optmodel;
number m{1..5, 1..3} = [[1 1] 1 [4 1] 1];
create data example
from [i j] = {setof{i in 1..2}<i**2>, {1, 2}} m;
proc print data=example noobs;
run;
The dummy parameter i in the SETOF expression takes precedence over the dummy parameter i declared in the key-columns item. The output from these statements is shown in Figure 5.12.
If no key-set is specified, then the set of index values is formed from the union of the index sets of the implicitly indexed columns. The number of index elements for each implicitly indexed array must match the number of key-columns. The type of each index element (string versus numeric) must match the element of the same position in other implicit indices.
The arrays for implicitly indexed columns in a CREATE DATA statement do not need to have identical index sets. A missing value is supplied for the value of an implicitly indexed array location when the implied index value is not in the array’s index set.
In the following statements, the key-set is unspecified. The set of index values is  , which is the union of the index sets of
, which is the union of the index sets of x and y. These index sets are not identical, so missing values are supplied when necessary. The results of these statements are shown
in Figure 5.13.
proc optmodel;
number x{1..2} init 2;
var y{2..3} init 3;
create data exdata from [keycol] x y;
proc print;
run;
The types of the output data set variables match the types of the source values. The output variable type for a key-columns matches the corresponding element type in the index value tuple. A numeric element matches a NUMERIC data set variable, while a string element matches a CHAR variable. For regular columns the source expression type determines the output data set variable type. A numeric expression produces a NUMERIC variable, while a string expression produces a CHAR variable.
Lengths of character variables in the output data set are determined automatically. The length is set to accommodate the longest string value output in that column.
You can use the iterated columns form to output selected rows of multiple arrays, assigning a different data set variable to each column. For example, the
following statements output the last two rows of the two-dimensional array, a, along with corresponding elements of the one-dimensional array, b:
proc optmodel;
num m = 3; /* number of rows/observations */
num n = 4; /* number of columns in a */
num a{i in 1..m, j in 1..n} = i*j; /* compute a */
num b{i in 1..m} = i**2; /* compute b */
set<num> subset = 2..m; /* used to omit first row */
create data out
from [i]=subset {j in 1..n}<col("a"||j)=a[i,j]> b;
The preceding statements create a data set out, which has  observations and
observations and  variables. The variables are named
variables. The variables are named i, a1 through an, and b, as shown in Figure 5.14.
Figure 5.14: CREATE DATA Set: The Iterated Column Form
See the section Data Set Input/Output for more examples of using the CREATE DATA statement.
DO Statement
-
DO ; statements ; END;
The DO statement groups a sequence of statements together as a single statement. Each statement within the list is executed sequentially. The DO statement can be used for grouping with the IF , FOR , and COFOR statements.
DO Statement, Iterative
-
DO name = specification-1
 , …specification-n
, …specification-n ![$\ms {]}$](images/ormpug_optmodel0027.png) ; statements ; END;
; statements ; END;
The iterative DO statement assigns the values from the sequence of specification items to a previously declared parameter or variable, name. The specified statement sequence is executed after each assignment. This statement corresponds to the iterative DO statement of the DATA step.
Each specification provides either a single number or a single string value, or a sequence of such values. Each specification takes the following form:
-
expression
 WHILE( logic-expression )
WHILE( logic-expression )  UNTIL( logic-expression )
UNTIL( logic-expression ) ![$\ms {]}$](images/ormpug_optmodel0027.png)
The expression in the specification provides a single value or set of values to assign to the target name. Multiple values can be provided for the loop by giving multiple specification items that are separated by commas. For example, the following statements output the values 1, 3, and 5:
proc optmodel;
number i;
do i=1,3,5;
put i;
end;
In this case, the same effect can be achieved with a single range expression in place of the explicit list of values, as in the following statements:
proc optmodel;
number i;
do i=1 to 5 by 2;
put 'value of i assigned by the DO loop = ' i;
i=i**2;
put 'value of i assigned in the body of the loop = ' i;
end;
The output of these statements is shown in Figure 5.15.
Figure 5.15: DO Loop: Name Parameter Unaffected
Unlike the DATA step, a range expression requires the limit to be specified. Additionally the BY part, if any, must follow the limit expression. Moreover, although the name parameter can be reassigned in the body of the loop, the sequence of values that is assigned by the DO loop is unaffected.
The argument expression can also be an expression that returns a set of numbers or strings. For example, the following statements produce the same
sequence of values for i as the previous statements but use a set parameter value:
proc optmodel;
set s = {1,3,5};
number i;
do i = s;
put i;
end;
Each specification can include a WHILE or UNTIL clause. A WHILE or UNTIL clause applies to the expression that immediately precedes the clause. The sequence that is specified by an expression can be terminated early by a WHILE or UNTIL clause. A WHILE logic-expression is evaluated for each sequence value before the nested statements. If the logic-expression returns a false (zero or missing) value, then the current sequence is terminated immediately. An UNTIL logic-expression is evaluated for each sequence value after the nested statements. The sequence from the current specification is terminated if the logic-expression returns a true value (nonzero and nonmissing). After early termination of a sequence due to a WHILE or UNTIL expression, the DO loop execution continues with the next specification, if any.
To demonstrate use of the WHILE clause, the following statements output the values 1, 2, and 3. In this case the sequence
of values from the set s is stopped when the value of i reaches 4.
proc optmodel;
set s = {1,2,3,4,5};
number i;
do i = s while(i NE 4);
put i;
end;
DO UNTIL Statement
-
DO UNTIL ( logic-expression ) ; statements ; END;
The DO UNTIL loop executes the specified sequence of statements repeatedly until the logic-expression, evaluated after the statements, returns true (a nonmissing nonzero value).
For example, the following statements output the values 1 and 2:
proc optmodel;
number i;
i = 1;
do until (i=3);
put i;
i=i+1;
end;
Multiple criteria can be introduced using expression operators, as in the following example:
do until (i=3 and j=7);
For a list of expression operators, see Table 5.10.
DO WHILE Statement
-
DO WHILE ( logic-expression ) ; statements ; END;
The DO WHILE loop executes the specified sequence of statements repeatedly as long as the logic-expression, evaluated before the statements, returns true (a nonmissing nonzero value).
For example, the following statements output the values 1 and 2:
proc optmodel;
number i;
i = 1;
do while (i<3);
put i;
i=i+1;
end;
Multiple criteria can be introduced using expression operators, as in the following example:
do while (i<3 and j<7);
For a list of expression operators, see Table 5.10.
DROP Statement
-
DROP identifier-list;
The DROP statement causes the solver to ignore a list of constraints, constraint arrays, or constraint array locations. The space-delimited identifier-list specifies the names of the dropped constraints. Each constraint, constraint array, or constraint array location is named by an identifier-expression. An entire constraint array is dropped if an identifier-expression omits the index for an array name.
The following example statements use the DROP statement:
proc optmodel;
var x{1..10};
con c1: x[1] + x[2] <= 3;
con disp{i in 1..9}: x[i+1] >= x[i] + 0.1;
drop c1; /* drops the c1 constraint */
drop disp[5]; /* drops just disp[5] */
drop disp; /* drops all disp constraints */
The constraint can be added back to the model with the RESTORE statement.
The following line drops both the c1 and disp[5] constraints:
drop c1 disp[5];
EXPAND Statement
-
EXPAND
 identifier-expression
identifier-expression ![$\ms {]}$](images/ormpug_optmodel0027.png)
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The EXPAND statement prints the specified constraint, variable, implicit variable, or objective declaration expressions in the current problem after expanding aggregation operators, substituting the current value for parameters and indices, and resolving constant subexpressions. identifier-expression is the name of a variable, objective, or constraint. If the name is omitted and no options are specified, then all variables, objectives, implicit variables, and undropped constraints in the current problem are printed. The following statements show an example EXPAND statement:
proc optmodel;
number n=2;
var x{1..n};
min z1=sum{i in 1..n}(x[i]-i)**2;
max z2=sum{i in 1..n}(i-x[i])**3;
con c{i in 1..n}: x[i]>=0;
fix x[2]=3;
expand;
These statements produce the output in Figure 5.16.
Figure 5.16: EXPAND Statement Output
Specifying an identifier-expression restricts output to the specified declaration. A non-array name prints only the specified item. If an array name is used with a specific index, then information for the specified array location is output. Using an array name without an index restricts output to all locations in the array.
You can use the following options to further control the EXPAND statement output:
- SOLVE
-
causes the EXPAND statement to print the variables, objectives, and constraints in the same form that would be seen by the solver if a SOLVE statement were executed. This includes any transformations by the PROC OPTMODEL presolver (see the section Presolver). In this form any fixed variables are replaced by their values. Unless an identifier-expression specifies a particular non-array item or array location, the EXPAND output is restricted to only the variables, the constraints, and the current problem objective.
The following options restrict the types of declarations output when no specific non-array item or array location is requested. By default, all types of declarations are output. Only the requested declaration types are output when one or more of the following options are used.
- CONSTRAINT | CON
- FIX
-
requests the output of fixed variables. These variables might have been fixed by the FIX statement (or by the presolver if the SOLVE option is specified). The FIX option can also be used in combination with the name of a variable array to display just the fixed elements of the array. - IIS
-
restricts the display to items found in the irreducible infeasible set (IIS) after the most recent SOLVE performed by the LP solver with the IIS=ON option. The IIS option for the EXPAND statement can also be used in combination with the name of a variable or constraint array to display only the elements of the array in the IIS. For more information about IIS, see the section Irreducible Infeasible Set. - IMPVAR
-
requests the output of implicit variables referenced in the current problem. - OBJECTIVE | OBJ
-
requests the output of objectives used in the current problem. This includes the current problem objective and any objectives referenced as implicit variables. - OMITTED
-
requests the output of variables that are referenced by problem equations but were not included in the current USE PROBLEM instance. The OPTMODEL procedure omits these variables from the generated problem.
- VAR
-
requests the output of unfixed variables. The VAR option can also be used in combination with the name of a variable array to display just the unfixed elements of the array.
For example, you can see the effect of a FIX statement on the problem that is presented to the solver by using the SOLVE option. You can modify the previous example as follows:
proc optmodel;
number n=2;
var x{1..n};
min z1=sum{i in 1..n}(x[i]-i)**2;
max z2=sum{i in 1..n}(i-x[i])**3;
con c{i in 1..n}: x[i]>=0;
fix x[2]=3;
expand / solve;
These statements produce the output in Figure 5.17.
Figure 5.17: Expansion with Fixed Variable
Compare the results in Figure 5.17 to those in Figure 5.16. The constraint c[1] has been converted to a variable bound. The subexpression that uses the fixed variable has been resolved to a constant.
FILE Statement
-
FILE file-specification
 LRECL=value
LRECL=value ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The FILE statement selects the current output file for the PUT statement. By default PUT output is sent to the SAS log. Use the FILE statement to manage a group of output files. The specified file is opened for output if it is not already open. The output file remains open until it is closed with the CLOSEFILE statement.
file-specification names the output file. It can use any of the following forms:
- ’external-file’
-
specifies the physical name of an external file in quotation marks. The interpretation of the filename depends on the operating environment. - file-name
-
specifies the logical name associated with a file by the FILENAME statement or by the operating environment. The names PRINT and LOG are reserved to refer to the SAS listing and log files, respectively.Note: Details about the FILENAME statement can be found in SAS Statements: Reference.
- ( expression )
-
specifies an expression that evaluates to a string that contains the physical name of an external file.
The LRECL= option sets the line length of the output file. The LRECL= option is ignored if the file is already open or if the PRINT or LOG file is specified.
The LRECL= value can be specified in these forms:
- integer
-
specifies the desired line length. - identifier-expression
-
specifies the name of a numeric parameter that contains the length. - ( expression )
-
specifies a numeric expression in parentheses that returns the line length.
The LRECL= value cannot exceed the largest four-byte signed integer, which is 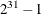 .
.
The following example shows how to use the FILE statement to handle multiple files:
proc optmodel;
file 'file.txt' lrecl=80; /* opens file.txt */
put 'This is line 1 of file.txt.';
file print; /* selects the listing */
put 'This goes to the listing.';
file 'file.txt'; /* reselects file.txt */
put 'This is line 2 of file.txt.';
closefile 'file.txt'; /* closes file.txt */
file log; /* selects the SAS log */
put 'This goes to the log.';
/* using expression to open and write a collection of files */
str ofile;
num i;
num l = 40;
do i = 1 to 3;
ofile = ('file' || i || '.txt');
file (ofile) lrecl=(l*i);
put ('This goes to ' || ofile);
closefile (ofile);
end;
The following statements illustrate the usefulness of using a logical name associated with a file by FILENAME statement:
proc optmodel; /* assigns a logical name to file.txt */ /* see FILENAME statement in */ /* SAS Statements: Reference */ filename myfile 'file.txt' mod; file myfile; put 'This is line 3 of file.txt.'; closefile myfile; file myfile; put 'This is line 4 of file.txt.'; closefile myfile;
Notice that the FILENAME statement opens the file referenced for append. Therefore, new data are appended to the end every
time the logical name, myfile, is used in the FILE statement.
FIX Statement
-
FIX identifier-list
 = ( expression )
= ( expression ) ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The FIX statement causes the solver to treat a list of variables, variable arrays, or variable array locations as fixed in
value. The identifier-list consists of one or more variable names separated by spaces. Each member of the identifier-list is fixed to the same expression. For example, the following statements fix the variables x and y to 3:
proc optmodel; var x, y; num a = 2; fix x y=(a+1);
A variable is specified with an identifier-expression (see the section Identifier Expressions). An entire variable array is fixed if the identifier-expression names an array without providing an index. A new value can be specified with the expression. If the expression is a constant, then the parentheses can be omitted. For example, the following statements fix all locations in array x to 0 except x[10], which is fixed to 1:
proc optmodel;
var x{1..10};
fix x = 0;
fix x[10] = 1;
If expression is omitted, the variable is fixed at its current value. For example, you can fix some variables to be their optimal values after the SOLVE statement is invoked. Note: The fixed value is equal to the current value for a fixed variable. The fixed value is updated if a new value is assigned to a fixed variable.
The effect of FIX can be reversed by using the UNFIX statement.
FOR Statement
-
FOR { index-set } statement;
The FOR statement executes its substatement for each member of the specified index-set . The index set can declare local dummy parameters. You can reference the value of these parameters in the substatement. For example, consider the following statements:
proc optmodel;
for {i in 1..2, j in {'a', 'b'}} put i= j=;
These statements produce the output in Figure 5.18.
As another example, the following statements set the current values for variable x to random values between 0 and 1:
proc optmodel;
var x{1..10};
for {i in 1..10}
x[i] = ranuni(-1);
Multiple statements can be controlled by specifying a DO statement group for the substatement.
Caution: Avoid modifying the parameters that are used by the FOR or COFOR statement index set from within the substatement. The set value that is used for the left-most index set item is not affected by such changes. However, the effect of parameter changes on later index set items cannot be predicted.
IF Statement
-
IF logic-expression THEN statement
 ELSE statement
ELSE statement ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The IF statement evaluates the logical expression and then conditionally executes the THEN or ELSE substatements. The substatement that follows the THEN keyword is executed when the logical expression result is nonmissing and nonzero. The ELSE substatement, if any, is executed when the logical expression result is a missing value or zero. The ELSE part is optional and must immediately follow the THEN substatement. When IF statements are nested, an ELSE is always matched to the nearest incomplete unmatched IF-THEN. Multiple statements can be controlled by using DO statements with the THEN or ELSE substatements.
Note: When an IF-THEN statement is used without an ELSE substatement, substatements of the IF statement are executed when possible as they are entered. Under certain circumstances, such as when an IF statement is nested in a FOR loop, the statement is not executed during interactive input until the next statement is seen. By following the IF-THEN statement with an extra semicolon, you can cause it to be executed upon submission, since the extra semicolon is handled as a null statement.
LEAVE Statement
-
LEAVE ;
The LEAVE statement terminates the execution of the entire loop body (iterative DO , DO UNTIL , DO WHILE , FOR , or COFOR ) that immediately contains the LEAVE statement. Execution resumes at the statement that follows the loop. The following example demonstrates a simple use of the LEAVE statement:
proc optmodel;
number i, j;
do i = 1..5;
do j = 1..4;
if i >= 3 and j = 2 then leave;
end;
print i j;
end;
The results from these statements are displayed in Figure 5.19.
For values of i equal to 1 or 2, the inner loop continues uninterrupted, leaving j with a value of 4. For values of i equal to 3, 4, or 5, the inner loop terminates early, leaving j with a value of 2.
Null Statement
-
;
The null statement is treated as a statement in the PROC OPTMODEL syntax, but its execution has no effect. It can be used as a placeholder statement.
PERFORMANCE Statement
-
PERFORMANCE options;
The PERFORMANCE statement controls the multithreaded and distributed execution features of PROC OPTMODEL and its solvers. The options that you specify in the PERFORMANCE statement are applied each time the statement is executed; they replace any previously specified options. For details about the options available for the PERFORMANCE statement, see the section PERFORMANCE Statement.
Within a COFOR loop, the PERFORMANCE statement controls solvers that are executed subsequently in the same COFOR iteration. The PERFORMANCE statement cannot specify distributed computing options in this context. If the COFOR loop is running in distributed mode, the options affect the solver as it runs in single-machine mode on the remote computing node. In distributed mode, the default NTHREADS= option value is equal to the number of threads on a node in the distributed computing environment. If the COFOR loop is running in multithreaded mode, the options affect execution of the solver on the machine that is running PROC OPTMODEL. In multithreaded mode, the default NTHREADS= option value is 1. In either mode, the NTHREADS= option value is limited to the number of threads in the COFOR loop execution environment.
PRINT Statement
-
PRINT print-items;
The PRINT statement outputs string and numeric data in tabular form. The statement specifies a list of arrays or other data items to print. Multiple items can be output together as data columns in the same table.
If no format is specified, the PRINT statement handles the details of formatting automatically (see the section Formatted Output for details). The default format for a numerical column is the fixed-point format (w.d format), which is chosen based on the values of the PDIGITS= and PWIDTH= options (see the section PROC OPTMODEL Statement) and on the values in the column. The PRINT statement uses scientific notation (the Ew. format) when a value is too large or too small to display in fixed format. The default format for a character column is the $w. format, where the width is set to be the length of the longest string (ignoring trailing blanks) in the column.
print-item can be specified in the following forms:
- identifier-expression
 format
format ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
specifies a data item to output. identifier-expression can name an array. In that case all defined array locations are output. format specifies a SAS format that overrides the default format. - ( expression )
 format
format ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
specifies a data value to output. format specifies a SAS format that overrides the default format. - { index-set } identifier-expression
 format
format ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
specifies a data item to output under the control of an index set . The item is printed as if it were an array with the specified set of indices. This form can be used to print a subset of the locations in an array, such as a single column. If the identifier-expression names an array, then the indices of the array must match the indices of the index-set. The format argument specifies a SAS format that overrides the default format. - { index-set } ( expression )
 format
format ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
specifies a data item to output under the control of an index set . The item is printed as if it were an array with the specified set of indices. In this form the expression is evaluated for each member of the index-set to create the array values for output. format specifies a SAS format that overrides the default format. - string
-
specifies a string value to print. - _PAGE_
-
specifies a page break.
The following example demonstrates the use of several print-item forms:
proc optmodel;
num x = 4.3;
var y{j in 1..4} init j*3.68;
print y; /* identifier-expression */
print (x * .265) dollar6.2; /* (expression) [format] */
print {i in 2..4} y; /* {index-set} identifier-expression */
print {i in 1..3}(i + i*.2345692) best7.;
/* {index-set} (expression) [format] */
print "Line 1"; /* string */
The output is displayed in Figure 5.20.
Figure 5.20: Print-item Forms
Adjacent print items that have similar indexing are grouped together and output in the same table. Items have similar indexing if they specify arrays that have the same number of indices and have matching index types (numeric versus string). Nonarray items are considered to have the same indexing as other nonarray items. The resulting table has a column for each array index followed by a column for each print item value. This format is called list form. For example, the following statements produce a list form table:
proc optmodel;
num a{i in 1..3} = i*i;
num b{i in 3..5} = 4*i;
print a b;
These statements produce the listing output in Figure 5.21.
The array index columns show the set of valid index values for the print items in the table. The array index column for the ith index is labeled [i]. There is a row for each combination of index values that was used. The index values are displayed in sorted ascending order.
The data columns show the array values that correspond to the index values in each row. If a particular array index is invalid or the array location is undefined, then the corresponding table entry is displayed as blank for numeric arrays and as an empty string for string arrays. If the print items are scalar, then the table has a single row and no array index columns.
If a table contains a single array print item, the array is two-dimensional (has two indices), and the array is dense enough, then the array is shown in matrix form. In this format there is a single index column that contains the row index values. The label of this column is blank. This column is followed by a column for every unique column index value for the array. The latter columns are labeled by the column value. These columns contain the array values for that particular array column. Table entries that correspond to array locations that have invalid or undefined combinations of row and column indices are blank or (for strings) printed as an empty string.
The following statements generate a simple example of matrix output:
proc optmodel;
print {i in 1..6, j in i..6} (i*10+j);
The PRINT statement produces the output in Figure 5.22.
Figure 5.22: Matrix Form PRINT Table
The PRINT statement prints single two-dimensional arrays in the form that uses fewer table cells (headings are ignored). Sparse arrays are normally printed in list form, and dense arrays are normally printed in matrix form. In a PROC OPTMODEL statement, the PMATRIX= option enables you to tune how the PRINT statement displays a two-dimensional array. The value of this option scales the total number of nonempty array elements, which is used to compute the tables cells needed for list form display. Specifying values for the PMATRIX= option less than 1 causes the list form to be used in more cases, while specifying values greater than 1 causes the matrix form to be used in more cases. If the value is 0, then the list form is always used. The default value of the PMATRIX= option is 1. Changing the default can be done with the RESET OPTIONS statement.
The following statements illustrate how the PMATRIX= option affects the display of the PRINT statement:
proc optmodel;
num a{i in 1..6, i..i} = i;
num b{i in 1..3, j in 1..3} = i*j;
print a;
print b;
reset options pmatrix=3;
print a;
reset options pmatrix=0.5;
print b;
The output is shown in Figure 5.23.
Figure 5.23: PRINT Statement: Effects of PMATRIX= Option
From Figure 5.23, you can see that, by default, the PRINT statement tries to make the display compact. However, you can change the default by using the PMATRIX= option.
PROFILE Statement
-
PROFILE
 mode
mode ![$\ms {]}$](images/ormpug_optmodel0027.png) options;
options;
The PROFILE statement controls the PROC OPTMODEL profiler, which enables you to collect and display timing and execution count information for PROC OPTMODEL processing. The profiler can be very useful for finding bottlenecks during execution, such as constraints that require large amounts of time during problem generation. When the profiler is enabled, PROC OPTMODEL records the time for processing a declaration, the time for executing statements, and the number of times that statements are executed. See Example 5.7: Sparse Modeling for an example use of the PROFILE statement.
The mode argument specifies the action that the PROFILE statement performs. You can use the following values for mode:
- ON
-
enables the profiler. Data are collected until the profiler is disabled or PROC OPTMODEL terminates. The profiler is also enabled when no mode is specified in a PROFILE statement. - OFF
-
disables the profiler. Note that the profiler is disabled when PROC OPTMODEL begins execution. -
prints the current accumulated profiler data. Items for declarations and statements are displayed in a table in descending order of their net time. Accumulated data are printed automatically when PROC OPTMODEL terminates.
The options control how PROC OPTMODEL collects and displays profiler information. Here are the valid options:
The elapsed time that is required to process an item includes the processing of other profiled items that it depends on. For example, the processing of a constraint during problem generation might require the evaluation of parameter values. The PROFILE statement reports net time so that the total of profiled times represents actual processing time.
The equation that is used to compute net time is
![\[ \mathrm{net\ time} = \mathrm{elapsed\ time} - \mathrm{nested\ time} - \mathrm{wait\ time} \]](images/ormpug_optmodel0040.png)
Elapsed time is the elapsed clock time this is required for processing an item. Nested time is the total of the elapsed times that are spent within the same thread to process other profiled items, such as substatements or declaration values. Wait time represents the time that a single thread is allocated but idle because it is waiting for other threads to perform the required processing. The total of net times can exceed the elapsed wall clock time when multiple threads are used.
PUT Statement
-
PUT
 put-items
put-items ![$\ms {]}$](images/ormpug_optmodel0027.png)
 @
@  @@
@@ ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The PUT statement writes text data to the current output file. The syntax of the PUT statement in PROC OPTMODEL is similar to the syntax of the PROC IML and DATA step PUT statements. The PUT statement contains a list of items that specify data for output and provide instructions for formatting the data.
The current output file is initially the SAS log. This can be overridden with the FILE statement. An output file can be closed with the CLOSEFILE statement.
Normally the PUT statement outputs the current line after processing all items. Final @ or @@ operators suppress this automatic line output and cause the current column position to be retained for use in the next PUT statement.
put-item can take any of the following forms.
- identifier-expression
 =
= ![$\ms {]}$](images/ormpug_optmodel0027.png)
 format
format ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
outputs the value of the parameter or variable that is specified by the identifier-expression . The equal sign (=) causes a name for the location to be printed before each location value.Normally each item value is printed in a default format. Any leading and trailing blanks in the formatted value are removed, and the value is followed by a blank space. When an explicit format is specified, the value is printed within the width determined by the format.
- name[*]
 .suffix
.suffix ![$\ms {]}$](images/ormpug_optmodel0027.png)
 =
= ![$\ms {]}$](images/ormpug_optmodel0027.png)
 format
format ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
outputs each defined location value for an array parameter. The array name is specified as in the identifier-expression form except that the index list is replaced by an asterisk (*). The equal sign (=) causes a name for the location to be printed before each location value along with the actual index values to be substituted for the asterisk.Each item value normally prints in a default format. Any leading and trailing blanks in the formatted value are removed, and the value is followed by a blank space. When an explicit format is specified, the value is printed within the width determined by the format.
- ( expression )
 =
= ![$\ms {]}$](images/ormpug_optmodel0027.png)
 format
format ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
outputs the value of the expression enclosed in parentheses. This produces similar results to the identifier-expression form except that the equal sign (=) uses the expression to form the name. - ’quoted-string’
-
copies the string to the output file. - @integer | identifier-expression | ( expression )
-
sets the absolute column position within the current line. The literal or expression value determines the new column position.
- +integer |identifier-expression|( expression )
-
sets the relative column position within the current line. The literal or expression value determines the amount to update the column position.
- /
-
outputs the current line and moves to the first column of the next line. - _PAGE_
-
outputs any pending line data and moves to the top of the next page.
QUIT Statement
-
QUIT ;
The QUIT statement terminates the OPTMODEL execution. The statement is executed immediately, so it cannot be a nested statement. A QUIT statement is implied when a DATA or PROC statement is read.
READ DATA Statement
-
READ DATA SAS-data-set
 NOMISS
NOMISS ![$\ms {]}$](images/ormpug_optmodel0027.png) INTO
INTO 
 set-name =
set-name = ![$\ms {]}$](images/ormpug_optmodel0027.png) [ read-key-columns ]
[ read-key-columns ] ![$\ms {]}$](images/ormpug_optmodel0027.png)
 read-columns
read-columns ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The READ DATA statement reads data from a SAS data set into PROC OPTMODEL parameter and variable locations. The arguments to the READ DATA statement are as follows:
- SAS-data-set
-
specifies the input data set name and options. You can specify the data set name and options directly or as the string value of an expression enclosed in parentheses. - set-name
-
specifies a set parameter in which to save the set of observation key values read from the input data set. - read-key-columns
-
provide the index values for array destinations. - read-columns
-
specify the data values to read and the destination locations.
The following example uses the READ DATA statement to copy data set variables j and k from the SAS data set indata into parameters of the same name. The READ= data set option specifies a password.
proc optmodel; number j, k; read data indata(read=secret) into j k;
Key Columns
If any read-key-columns are specified, then the READ DATA statement reads all observations from the input data set. If no read-key-columns are specified, then only the first observation of the data set is read. The data set is closed after reading the requested information.
Each read-key-column declares a local dummy parameter and specifies a data set variable that supplies the column value. The values of the specified data set variables from each observation are combined into a key tuple. This combination is known as the observation key. The observation key is used to index array locations specified by the read-columns items. The observation key is expected to be unique for each observation read from the data set.
The syntax for a read-key-column is as follows:
-
name
 = source-name
= source-name ![$\ms {]}$](images/ormpug_optmodel0027.png)
 / trim-option
/ trim-option ![$\ms {]}$](images/ormpug_optmodel0027.png)
A read-key-column creates a local dummy parameter named name that holds an element of the observation key tuple. The dummy parameter can be used in subsequent read-columns items to reference the element value. If a source-name is given, then it specifies the data set variable that supplies the value. Otherwise the source data set variable has the
same name as the dummy parameter, name. Use the special data set variable name _N_ to refer to the number identification of the observations.
You can specify a set-name to save the set of observation keys into a set parameter. If the observation key consists of a single scalar value, then the set member type must match the scalar type. Otherwise the set member type must be a tuple with element types that match the corresponding observation key element types.
The READ DATA statement initially assigns an empty set to the target set-name parameter. As observations are read, a tuple for each observation key is added to the set. A set used to index an array destination
in the read-columns can be read at the same time as the array values. Consider a data set, invdata, created by the following statements:
data invdata; input item $ invcount; datalines; table 100 sofa 250 chair 80 ;
The following statements read the data set invdata, which has two variables, item and invcount. The READ DATA statement constructs a set of inventory items, Items. At the same time, the parameter location invcount[item] is assigned the value of the data set variable invcount in the corresponding observation.
proc optmodel;
set<string> Items;
number invcount{Items};
read data invdata into Items=[item] invcount;
print invcount;
The output of these statements is shown in Figure 5.24.
When observations are read, the values of data set variables are copied to parameter locations. Numeric values are copied unchanged. For character values, trim-option controls how leading and trailing blanks are processed. trim-option is ignored when the value type is numeric. Specify any of the following keywords for trim-option:
Columns
read-columns specify data set variables to read and PROC OPTMODEL parameter locations to which to assign the values. The types of the input data set variables must match the types of the parameters. Array parameters can be implicitly or explicitly indexed by the observation key values.
Normally, missing values from the data set are assigned to the parameters that are specified in the read-columns. The NOMISS keyword suppresses the assignment of missing values, leaving the corresponding parameter locations unchanged. Note that the parameter location does not need to have a valid index in this case. This permits a single statement to read data into multiple arrays that have different index sets.
read-columns have the following forms:
- identifier-expression
 = name
= name  COL( name-expression )
COL( name-expression ) ![$\ms {]}$](images/ormpug_optmodel0027.png)
 / trim-option
/ trim-option ![$\ms {]}$](images/ormpug_optmodel0027.png)
-
transfers an input data set variable to a target parameter or variable. identifier-expression specifies the target. If the identifier-expression specifies an array without an explicit index, then the observation key provides an implicit index. The name of the input data set variable can be specified with a name or a COL expression. Otherwise the data set variable name is given by the name part of the identifier-expression. For COL expressions, the string-valued name-expression is evaluated to determine the data set variable name. trim-option controls removal of leading and trailing blanks in the incoming data. For example, the following statements read the data set variablescolumn1andcolumn2from the data setexdatainto the PROC OPTMODEL parameterspandq, respectively. The observation numbers inexdataare read into the setindx, which indexespandq.data exdata; input column1 column2; datalines; 1 2 3 4 ;
proc optmodel; number n init 2; set<num> indx; number p{indx}, q{indx}; read data exdata into indx=[_N_] p=column1 q=col("column"||n); print p q;The output is shown in Figure 5.25.
- { index-set } < read-columns >
-
performs the transfers by iterating each column specified by <read-columns> for each member of the index-set . If there are n columns and m index set members, then columns are generated. The dummy parameters from the index set can be used in the columns to generate distinct input data
set variable names in the iterated columns, using COL expressions. The columns are expanded when the READ DATA statement is
executed, before any observations are read. This form of read-columns cannot be nested. In other words, the following form of read-columns is NOT allowed:
columns are generated. The dummy parameters from the index set can be used in the columns to generate distinct input data
set variable names in the iterated columns, using COL expressions. The columns are expanded when the READ DATA statement is
executed, before any observations are read. This form of read-columns cannot be nested. In other words, the following form of read-columns is NOT allowed:
{ index-set } < { index-set } < read-columns > >
An example that demonstrates the use of the iterated column read-option follows.
You can use an iterated column read-option to read multiple data set variables into the same array. For example, a data set might store an entire row of array data in a group of data set variables. The following statements demonstrate how to read a data set that contains demand data divided by day:
data dmnd;
input loc $ day1 day2 day3 day4 day5;
datalines;
East 1.1 2.3 1.3 3.6 4.7
West 7.0 2.1 6.1 5.8 3.2
;
proc optmodel;
set DOW = 1..5; /* days of week, 1=Monday, 5=Friday */
set<string> LOCS; /* locations */
number demand{LOCS, DOW};
read data dmnd
into LOCS=[loc]
{d in DOW} < demand[loc, d]=col("day"||d) >;
print demand;
These statements read a set of demand variables named DAY1–DAY5 from each observation, filling in the two-dimensional array demand. The output is shown in Figure 5.26.
RESET OPTIONS Statement
-
RESET OPTIONS options;
-
RESET OPTION options;
The RESET OPTIONS statement sets PROC OPTMODEL option values or restores them to their defaults. Options can be specified by using the same syntax as in the PROC OPTMODEL statement. The RESET OPTIONS statement provides two extensions to the option syntax. If an option normally requires a value (specified with an equal sign (=) operator), then specifying the option name alone resets it to its default value. You can also specify an expression enclosed in parentheses in place of a literal value. See the section OPTMODEL Options for an example.
The RESET OPTIONS statement can be placed inside loops or conditional statements. The statement is applied each time it is executed.
RESTORE Statement
-
RESTORE identifier-list;
The RESTORE statement adds a list of constraints, constraint arrays, or constraint array locations that were dropped by the DROP statement back into the solver model, or includes constraints in a problem where they were not previously present. The space-delimited identifier-list specifies the names of the constraints. Each constraint, constraint array, or constraint array location is named by an identifier-expression. An entire constraint array is restored if an identifier-expression omits the index from an array name. For example, the following statements declare a constraint array and then drop it:
con c{i in 1..4}: x[i] + y[i] <=1;
drop c;
The following statement restores the first constraint:
restore c[1];
The following statement restores the second and third constraints:
restore c[2] c[3];
If you want to restore all of the constraints, you can submit the following statement:
restore c;
SAVE MPS Statement
-
SAVE MPS SAS-data-set
 ( OBJECTIVE
( OBJECTIVE  OBJ ) name
OBJ ) name ![$\ms {]}$](images/ormpug_optmodel0027.png)
 ( NOOBJECTIVE
( NOOBJECTIVE  NOOBJ )
NOOBJ ) ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The SAVE MPS statement saves the structure and coefficients for a linear programming model into a SAS data set. This data set can be used as input data for the OPTLP or OPTMILP procedure.
Note: The OPTMODEL presolver (see the section Presolver) is automatically bypassed so that the statement saves the original model without eliminating fixed variables, tightening bounds, and so on.
The SAS-data-set argument specifies the output data set name and options. You can specify the data set name and options directly or as the string value of an expression enclosed in parentheses. The output data set uses the MPS format described in Chapter 17: The MPS-Format SAS Data Set. The generated data set contains observations that define different parts of the linear program.
Variables, constraints, and objectives are referenced in the data set by using label text from the corresponding .label suffix value. The default text is based on the name in the model. See the section Suffixes for more details. Labels are limited by default to 32 characters and are abbreviated to fit. You can change the maximum length
for labels by using the MAXLABLEN=
option. When needed, a programmatically generated number is added to labels to avoid duplication.
If the OBJECTIVE keyword is used, the objective name becomes the current problem objective. If the NOOBJECTIVE keyword is used or the current problem does not have an objective, then the data set includes a default constant zero objective. Otherwise, the current problem objective is included in the data set.
When an integer variable has been assigned a nondefault branching priority or direction, the MPS data set includes a BRANCH section. See Chapter 17: The MPS-Format SAS Data Set, for more details.
The following statements show an example of the SAVE MPS statement. The model is specified using the OPTMODEL procedure. Then
it is saved as the MPS data set MPSData, as shown in Figure 5.27. Next, PROC OPTLP is used to solve the resulting linear program.
proc optmodel; var x >= 0, y >= 0; con c: x >= y; con bx: x <= 2; con by: y <= 1; min obj=0.5*x-y; save mps MPSData; quit; proc optlp data=MPSData pout=PrimalOut dout=DualOut; run;
Figure 5.27: The MPS Data Set Generated by SAVE MPS Statement
SAVE QPS Statement
-
SAVE QPS SAS-data-set
 ( OBJECTIVE
( OBJECTIVE  OBJ ) name
OBJ ) name ![$\ms {]}$](images/ormpug_optmodel0027.png)
 ( NOOBJECTIVE
( NOOBJECTIVE  NOOBJ )
NOOBJ ) ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The SAVE QPS statement saves the structure and coefficients for a quadratic programming model into a SAS data set. This data set can be used as input data for the OPTQP procedure.
Note: The OPTMODEL presolver (see the section Presolver) is automatically bypassed so that the statement saves the original model without eliminating fixed variables, tightening bounds, and so on.
The SAS-data-set argument specifies the output data set name and options. You can specify the data set name and options directly or as the string value of an expression enclosed in parentheses. The output data set uses the QPS format described in Chapter 17. The generated data set contains observations that define different parts of the quadratic program.
Variables, constraints, and objectives are referenced in the data set by using label text from the corresponding .label suffix value. The default text is based on the name in the model. See the section Suffixes for more details. Labels are limited by default to 32 characters and are abbreviated to fit. You can change the maximum length
for labels by using the MAXLABLEN=
option. When needed, a programmatically generated number is added to labels to avoid duplication.
If the OBJECTIVE keyword is used, the objective name becomes the current problem objective. If the NOOBJECTIVE keyword is used or the current problem does not have an objective, then the data set includes a default constant zero objective. Otherwise, the current problem objective is included in the data set. The quadratic coefficients of the objective function appear in the QSECTION section of the output data set.
The following statements show an example of the SAVE QPS statement. The model is specified using the OPTMODEL procedure. Then
it is saved as the QPS data set QPSData, as shown in Figure 5.28. Next, PROC OPTQP is used to solve the resulting quadratic program.
proc optmodel;
var x{1..2} >= 0;
min z = 2*x[1] + 3 * x[2] + x[1]**2 + 10*x[2]**2
+ 2.5*x[1]*x[2];
con c1: x[1] - x[2] <= 1;
con c2: x[1] + 2*x[2] >= 100;
save qps QPSData;
quit;
proc optqp data=QPSData pout=PrimalOut dout=DualOut;
run;
Figure 5.28: QPS Data Set Generated by the SAVE QPS Statement
| Obs | FIELD1 | FIELD2 | FIELD3 | FIELD4 | FIELD5 | FIELD6 |
|---|---|---|---|---|---|---|
| 1 | NAME | QPSData | . | . | ||
| 2 | ROWS | . | . | |||
| 3 | N | z | . | . | ||
| 4 | L | c1 | . | . | ||
| 5 | G | c2 | . | . | ||
| 6 | COLUMNS | . | . | |||
| 7 | x[1] | z | 2.0 | c1 | 1 | |
| 8 | x[1] | c2 | 1.0 | . | ||
| 9 | x[2] | z | 3.0 | c1 | -1 | |
| 10 | x[2] | c2 | 2.0 | . | ||
| 11 | RHS | . | . | |||
| 12 | .RHS. | c1 | 1.0 | . | ||
| 13 | .RHS. | c2 | 100.0 | . | ||
| 14 | QSECTION | . | . | |||
| 15 | x[1] | x[1] | 2.0 | . | ||
| 16 | x[1] | x[2] | 2.5 | . | ||
| 17 | x[2] | x[2] | 20.0 | . | ||
| 18 | ENDATA | . | . |
SOLVE Statement
-
SOLVE
 WITH solver
WITH solver ![$\ms {]}$](images/ormpug_optmodel0027.png)
 ( OBJECTIVE | OBJ ) name
( OBJECTIVE | OBJ ) name ![$\ms {]}$](images/ormpug_optmodel0027.png)
 ( NOOBJECTIVE | NOOBJ )
( NOOBJECTIVE | NOOBJ ) ![$\ms {]}$](images/ormpug_optmodel0027.png)
 RELAXINT
RELAXINT ![$\ms {]}$](images/ormpug_optmodel0027.png)
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The SOLVE statement invokes a PROC OPTMODEL solver. The current model is first resolved to the numeric form that is required by the solver. The resolved model and possibly the current values of any optimization variables are passed to the solver. After the solver finishes executing, the SOLVE statement prints a short table that shows a summary of results from the solver (see the section ODS Table and Variable Names) and updates the _OROPTMODEL_ macro variable.
Here are the arguments to the SOLVE statement:
Table 5.8: Default Solvers and Algorithms in PROC OPTMODEL
|
Problem |
Solver |
Algorithm |
|
Constraint programming |
CLP |
Constraint propagation and backtracking search |
|
Linear programming |
LP |
Dual simplex |
|
Mixed integer linear programming |
MILP |
Branch-and-cut |
|
General nonlinear programming |
NLP |
Interior point NLP |
|
Quadratic programming |
QP |
Interior point QP |
- name
-
specifies the objective to use. This sets the current objective for the problem. You can abbreviate the OBJECTIVE keyword as OBJ. If this argument is not specified, then the problem objective is unchanged. - NOOBJECTIVE
-
requests that the solver ignore the current objective for the problem and use a constant zero objective instead. This keyword enables the solver to process the current model as a feasibility problem. You can abbreviate the NOOBJECTIVE keyword as NOOBJ.
- RELAXINT
-
requests that any integral variables be relaxed to be continuous. RELAXINT can be used with linear and nonlinear problems in addition to any solver.
- options
-
specifies solver options. You can specify solver options directly only when you use the WITH clause. A list of the options available with the solver is provided in the individual chapters that describe each solver. Table 5.9 lists the available option types. You can use an expression in parentheses in place of a literal option value for numeric and keyword options. A string expression is matched to a keyword. OPTMODEL parameters that are changed by the solver must be specified by a parameter or array option.
Table 5.9: Solver Option Types
|
Type |
Syntax |
Example |
|
Boolean |
option | NOoption |
solve with nlp / NOMULTISTART; |
|
Keyword |
option=name |
solve with lp / ALGORITHM=PS; |
|
Numeric |
option=number |
solve with nlp / OPTTOL=1E–4; |
|
Parameter |
option=identifier-expression |
solve with network / links=(INCLUDE=LINKS) concomp; |
|
Array |
option=array-name |
solve with network / links=(WEIGHT=WEIGHT) tsp; |
The SOLVE statement uses the value of the predeclared _SOLVER_OPTIONS_ and _solver_OPTIONS_ string parameters to provide default solver options. Any options that are specified by these parameters are added before options that are specified in the SOLVE statement, with options from _SOLVER_OPTIONS_ appearing first. These options are included even when the SOLVE statement does not contain a WITH clause to specify a solver; in this case, solver is the name of the default solver as shown in Table 5.8.
Initially the predeclared string parameters _SOLVER_OPTIONS_ and _solver_OPTIONS_ (for each solver) are empty strings, but you can assign them. You must use keywords or literal values to specify option values in these strings. Redundant white space is allowed. For example, the following statements set up some simple defaults:
_SOLVER_OPTIONS_ = "MAXTIME = 600"; /* options for all solvers */ _LP_OPTIONS_ = "PRESOLVER=AGGRESSIVE"; /* options for LP solver */
Optimization techniques that use initial values obtain them from the current values of the optimization variables unless the NOINITVAR option is specified. When the solver finishes executing, the current value of each optimization variable is replaced by the optimal value found by the solver. These values can then be used as the initial values for subsequent solver invocations.
Note: If a solver fails, any currently pending statement is stopped and processing continues with the next complete statement read from the input. For example, if a SOLVE statement that is enclosed in a DO group (see the section DO Statement) fails, then the subsequent statements in the group are not executed and processing resumes at the point immediately following the DO group. Neither an infeasible result, an unbounded result, nor reaching an iteration limit is considered to be a solver failure.
Note: The information that appears in the macro variable _OROPTMODEL_ (see the section Macro Variable _OROPTMODEL_) varies by solver.
Note: The RELAXINT keyword is applied immediately before the problem is passed to the solver, after any processing by the PROC OPTMODEL presolver. So the problem presented to the solver might not be equivalent to the one produced by setting the .RELAX suffix of all variables to a nonzero value. In particular, the bounds of integer variables are still adjusted to be integral, and PROC OPTMODEL’s presolver might use integrality to tighten bounds further.
STOP Statement
-
STOP ;
The STOP statement halts the execution of all statements that contain it, including DO statements and other control or looping statements. Execution continues with the next top-level source statement. The following statements demonstrate a simple use of the STOP statement:
proc optmodel;
number i, j;
do i = 1..5;
do j = 1..4;
if i = 3 and j = 2 then stop;
end;
end;
print i j;
The output is shown in Figure 5.29.
When the counters i and j reach 3 and 2, respectively, the STOP statement terminates both loops. Execution continues with the PRINT statement.
SUBMIT Statement
-
SUBMIT arguments
 / options
/ options ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
-
SAS statements;
-
ENDSUBMIT ;
The SUBMIT statement allows SAS code to be executed before PROC OPTMODEL processing continues. For example, you can use the SUBMIT statement to invoke other SAS procedures to perform analysis or to display results. The following statements use PROC SORT to order a list of nodes by decreasing priority; the nodes can be used for further processing:
proc optmodel;
set<str> NODES;
num priority{NODES};
/* set up priority data... */
/* sort nodes by descending priority */
create data temppri from [id] priority;
submit;
proc sort;
by descending priority;
run;
endsubmit;
/* load nodes by priority */
str nodesByPri{i in 1..card(NODES)};
read data temppri into [_n_] nodesByPri=id;
/* use the sorted list... */
The SUBMIT statement must appear as the last or only statement on a line. It is followed by lines of SAS statements, terminated by the ENDSUBMIT statement on a line of its own. The SAS statements between the SUBMIT and ENDSUBMIT statements are referred to as a SUBMIT block. The SUBMIT block is sent to the SAS language processor each time the SUBMIT statement is executed.
The SUBMIT block can include SAS global statements and procedure and invocations. Macros are not expanded until the SUBMIT block is executed. So you can change macro variables to modify the behavior of the SUBMIT block each time it is processed.
The arguments list specifies macro variables to initialize in the SUBMIT block environment before the SUBMIT block is executed. List items are separated by spaces. Each of the arguments takes one of the following forms:
- name
-
copies the value of the PROC OPTMODEL parameter name to the macro variable that has the same name. - name = identifier-expression
-
copies the value of the PROC OPTMODEL parameter specified by identifier-expression to the macro variable name. - name = number | "string" | 'string'
-
copies the value of the specified number or string constant to the macro variable name. - name = ( expression )
-
copies the result of evaluating expression to the macro variable name.
The following statements use a SUBMIT argument to modify the output each time the SUBMIT block is invoked:
for {i in 1..5}
submit a=i;
%put Value of a is &a..;
endsubmit;
The options in the SUBMIT statement are used to retrieve status information after a SUBMIT block is executed. Each item in the space-delimited options list has one of the following forms:
- OK = identifier-expression
-
specifies a PROC OPTMODEL numeric parameter location, identifier-expression, that is updated to indicate the success of the SUBMIT block execution. The location is set to 1 if execution is successful or 0 if errors are detected. PROC OPTMODEL continues execution when the SUBMIT block encounters errors only if the OK= option is specified. - OUT
 =
= ![$\ms {]}$](images/ormpug_optmodel0027.png) output-argument
output-argument -
specifies a single output-argument for retrieving macro variable values from the SUBMIT block environment after each execution of the block. - OUT
 =
= ![$\ms {]}$](images/ormpug_optmodel0027.png) ( output-argument )
( output-argument ) -
specifies a list of space-delimited output-arguments for retrieving macro variable values from the SUBMIT block environment after the block is executed.
Each output-argument item specifies a macro variable to copy out of the SUBMIT block environment after the block is executed. Each item takes one of the following two forms:
- identifier-expression
-
copies the macro variable specified by the name portion of the identifier-expression into the PROC OPTMODEL parameter location specified by identifier-expression. - identifier-expression = name
-
copies the macro variable specified by name into the PROC OPTMODEL parameter location specified by identifier-expression.
The following statements show how to use the options in the SUBMIT statement to retrieve the result of a SUBMIT block execution:
proc optmodel;
num success, syscc;
submit / OK = success out syscc;
data example;
set notfound;
j = i*i;
run;
endsubmit;
print success syscc;
The DATA step fails, so the success parameter is set to 0 and syscc is set to the error code in the &SYSCC macro variable. The output is shown in Figure 5.30.
Note: The SUBMIT block runs in an environment that is nested in the environment that the OPTMODEL procedure is running in. Resources from the PROC OPTMODEL environment are initially visible in the nested environment. However, the nested environment can have its own local values for options, LIBNAME librefs, FILENAME filerefs, titles, footnotes, and macros. For example, the nested environment has its own global macro scope, which can hide macros visible in the outer environment. The output-arguments of the SUBMIT statement options can retrieve the values of macros defined in this scope.
Note: A SUBMIT block can reset the ODS environment of the OPTMODEL procedure. For example, the ODS SELECT and EXCLUDE lists could be cleared after the SUBMIT block executes.
Note: A SUBMIT statement can appear only in open code. An error message is displayed if the SUBMIT statement is read from a macro. You can avoid this limitation by placing the SUBMIT statement, SUBMIT block, and ENDSUBMIT in a separate file and by using the %INCLUDE statement to include the file in the macro.
UNFIX Statement
-
UNFIX identifier-list
 = ( expression )
= ( expression ) ![$\ms {]}$](images/ormpug_optmodel0027.png) ;
;
The UNFIX statement reverses the effect of FIX statements. The solver can vary the specified variables, variable arrays, or variable array locations specified by identifier-list. The identifier-list consists of one or more variable names separated by spaces.
Each variable name in the identifier-list is an identifier expression (see the section Identifier Expressions). The UNFIX statement affects an entire variable array if the identifier expression omits the index from an array name. The expression specifies a new initial value that is stored in each element of the identifier-list.
The following example demonstrates the UNFIX command:
proc optmodel;
var x{1..3};
fix x; /* fixes entire array to 0 */
unfix x[1]; /* x[1] can now be varied again */
unfix x[2] = 2; /* x[2] is given an initial value 2 */
/* and can be varied now */
unfix x; /* all x indices can now be varied */
After the following statements are executed, the variables x[1] and x[2] are not fixed. They each hold the value 4. The variable x[3] is fixed at a value of 2.
proc optmodel;
var x{1..3} init 2;
num a = 1;
fix x;
unfix x[1] x[2]=(a+3);
USE PROBLEM Statement
-
USE PROBLEM identifier-expression;
The USE PROBLEM programming statement makes the problem specified by the identifier-expression be the current problem. If the problem has not been previously used, the problem is created using the PROBLEM declaration corresponding to the name. The problem must have been previously declared.
[1] The OPTMODEL procedure never uses the network solver as a default. If the QP solver detects nonconvexity (nonconcavity) for a minimization (maximization) problem, then PROC OPTMODEL calls the NLP solver instead.
