The Nonlinear Programming Solver

The following data are used to build a regression model:

data samples;
   input x1 x2 y;
   datalines;
 4  8   43.71
62  5  351.29
81 62 2878.91
85 75 3591.59
65 54 2058.71
96 84 4487.87
98 29 1773.52
36 33  767.57
30 91 1637.66
 3 59  215.28
62 57 2067.42
11 48  394.11
66 21  932.84
68 24 1069.21
95 30 1770.78
34 14  368.51
86 81 3902.27
37 49 1115.67
46 80 2136.92
87 72 3537.84
;

Suppose you want to compute the parameters in your regression model based on the preceding data, and the model is

where 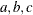are the parameters that need to be found.

The following PROC OPTMODEL call specifies the least squares problem for the regression model:

/* Reqression model with interactive term: y = a*x1 + b*x2 + c*x1*x2 */
proc optmodel;
   set obs;
   num x1{obs}, x2{obs}, y{obs};
   num mycov{i in 1.._nvar_, j in 1..i};
   var a, b, c;
   read data samples into obs=[_n_] x1 x2 y;
   impvar Err{i in obs} = y[i] - (a*x1[i]+b*x2[i]+c*x1[i]*x2[i]);
   min f = sum{i in obs} Err[i]^2;
   solve with nlp/covest=(cov=5 covout=mycov);
   print mycov;
   print a b c;
quit;

The solution is displayed in Figure 10.7.