| The OPTQP Procedure |
Example 17.1: Linear Least-Squares Problem
The linear least-squares problem arises in the context of determining a solution to an over-determined set of linear equations. In practice, these could arise in data fitting and estimation problems. An 1 system of linear equations can be defined as
This problem is called a least-squares problem for the following reason. Let ![]() ,
, ![]() , and
, and ![]() be defined as previously. Let
be defined as previously. Let ![]() be the
be the ![]() th component of the vector
th component of the vector ![]() :
:
You can create the QPS-format input data set by using the following SAS code:
data lsdata;
input field1 $ field2 $ field3$ field4 field5 $ field6 @;
datalines;
NAME . LEASTSQ . . .
ROWS . . . . .
N OBJ . . . .
G EQ3 . . . .
COLUMNS . . . . .
. X1 OBJ -14 EQ3 3
. X2 OBJ -4 EQ3 2
RHS . . . . .
. RHS OBJ -2 EQ3 0.9
RANGES . . . . .
. RNG EQ3 0.2 . .
BOUNDS . . . . .
FR BND1 X1 . . .
FR BND1 X2 . . .
QUADOBJ . . . . .
. X1 X1 52 . .
. X1 X2 10 . .
. X2 X2 10 . .
ENDATA . . . . .
;
The decision variables ![]() and
and ![]() are free, so they have bound type FR in the BOUNDS section of the QPS-format data set.
are free, so they have bound type FR in the BOUNDS section of the QPS-format data set.
You can use the following SAS code to solve the least-squares problem:
proc optqp data=lsdata
primalout = lspout;
run;
The optimal solution is displayed in Output 17.1.1.
Output 17.1.1: Solution to the Least-Squares ProblemThe iteration log is shown in Output 17.1.2.
Output 17.1.2: Iteration Log
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
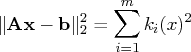
![\mathbf{a} = [4 & 0 \ -1 & 1 \ 3 & 2 ], \mathbf{b} = [1 \ 0 \ 1 ]](images/optqp_optqpeq87.gif)