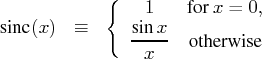The Unconstrained Nonlinear Programming Solver

Overview

The unconstrained nonlinear programming solver (NLPU) is a component of the OPTMODEL procedure, and it can be used for solving general unconstrained nonlinear programming (NLP) problems.

Mathematically, an unconstrained nonlinear programming problem can be stated as follows:

$\displaystyle\mathop{\rm minimize}_{x\in{\mathbb r}^n} & f(x) \$

where $x \in \mathbb{r}^n$ is the vector of decision variables and

: $\mathbb{r}^n\mapsto\mathbb{r}$ is the nonlinear objective function.

is assumed to be twice continuously differentiable, meaning that its second derivatives exist and are continuous in $\mathbb{r}^n$ .

For purely unconstrained optimization, PROC OPTMODEL implements the following algorithms:

Fletcher-Reeves nonlinear conjugate gradient algorithm for convex unconstrained optimization
Polak-Ribière nonlinear conjugate gradient algorithm for convex unconstrained optimization
Limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm for general nonconvex unconstrained optimization (default)

If the objective function is convex , then the optimal solution is a global optimum; otherwise it is a local optimum. In other words, the optimal solution obtained by the NLPU solver depends on the starting point. An example of a nonlinear function with multiple local optima is displayed in Figure 11.1.

Figure 11.1: An Example of Multiple Local Optimal Points

The function displayed in Figure 11.1 is

$f(x, y) = {sinc}\,(x^2 + y^2) + {sinc}\,((x - 2)^2 + y^2)$

where sinc(.), also called the "sampling function," is a function that arises frequently in signal processing. The function is defined as

${sinc}(x) & \equiv & \{1 & {for}\, x = 0,\ \displaystyle\frac{{sin}\, x}x & {otherwise}\ . \$

Top of Page