PROC NLP: Example 4.8: Chemical Equilibrium :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The NLP Procedure

Example 4.8: Chemical Equilibrium

The following example is used in many test libraries for nonlinear programming and was taken originally from Bracken and McCormick (1968).

The problem is to determine the composition of a mixture of various chemicals satisfying its chemical equilibrium state. The second law of thermodynamics implies that a mixture of chemicals satisfies its chemical equilibrium state (at a constant temperature and pressure) when the free energy of the mixture is reduced to a minimum. Therefore the composition of the chemicals satisfying its chemical equilibrium state can be found by minimizing the function of the free energy of the mixture.

Notation:

	number of chemical elements in the mixture
	number of compounds in the mixture
	number of moles for compound ,
	total number of moles in the mixture $(s = \sum_{i=1}^n x_j)$
$a_{ij}$	number of atoms of element in a molecule of compound
	atomic weight of element in the mixture

Constraints for the Mixture:

The number of moles must be positive:
$x_j \gt 0 , j=1, ... ,n$
There are 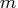mass balance relationships,
$\sum_{j=1}^n a_{ij} x_j = b_i , i=1, ... ,m$

Objective Function: Total Free Energy of Mixture

$f(x) = \sum_{j=1}^n x_j [c_j + \ln ( \frac{x_j}s ) ]$

with

$c_j = ( \frac{f^{\circ}}{rt} ) _j + \ln p$

where $f^{\circ}/rt$ is the model standard free energy function for the th compound (found in tables) and is the total pressure in atmospheres.

Minimization Problem:

Determine the parameters that minimize the objective function subject to the nonnegativity and linear balance constraints.

Numeric Example:

Determine the equilibrium composition of compound $\frac{1}2 n_2h_4 + \frac{1}2 o_2$ at temperature $t= 3500^{\circ}{\rm k}$ and pressure $p= 750{\rm psi}$ .

				$a_{ij}$

	Compound	$(f^{\circ} / rt)_j$
1		-10.021	-6.089	1
2		-21.096	-17.164	2
3		-37.986	-34.054	2		1
4		-9.846	-5.914		1
5		-28.653	-24.721		2
6		-18.918	-14.986	1	1
7		-28.032	-24.100		1	1
8		-14.640	-10.708			1
9		-30.594	-26.662			2
10		-26.111	-22.179	1		1

Example Specification:

  
    proc nlp tech=tr pall; 
       array c[10] -6.089 -17.164 -34.054  -5.914 -24.721 
                  -14.986 -24.100 -10.708 -26.662 -22.179; 
       array x[10] x1-x10; 
       min y; 
       parms x1-x10 = .1; 
       bounds 1.e-6 <= x1-x10; 
       lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10, 
              1. = x4 + 2. * x5 + x6 + x7, 
              1. = x3 + x7  + x8 + 2. * x9 + x10; 
       s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10; 
       y = 0.; 
       do j = 1 to 10; 
          y = y + x[j] * (c[j] + log(x[j] / s)); 
       end; 
    run;

Displayed Output:

The iteration history given in Output 4.8.1 does not show any problems.

Output 4.8.1: Iteration History

Trust Region Optimization

Without Parameter Scaling

Iteration	Function Calls	Active Constraints		Objective Function	Objective Function Change	Max Abs Gradient Element	Lambda	Trust Region Radius
1	2	3	'	-47.33412	2.2790	6.0765	2.456	1.000
2	3	3	'	-47.70043	0.3663	8.5592	0.908	0.418
3	4	3		-47.73074	0.0303	6.4942	0	0.359
4	5	3		-47.73275	0.00201	4.7606	0	0.118
5	6	3		-47.73554	0.00279	3.2125	0	0.0168
6	7	3		-47.74223	0.00669	1.9552	110.6	0.00271
7	8	3		-47.75048	0.00825	1.1157	102.9	0.00563
8	9	3		-47.75876	0.00828	0.4165	3.787	0.0116
9	10	3		-47.76101	0.00224	0.0716	0	0.0121
10	11	3		-47.76109	0.000083	0.00238	0	0.0111
11	12	3		-47.76109	9.609E-8	2.733E-6	0	0.00248

Optimization Results
Iterations	11	Function Calls	13
Hessian Calls	12	Active Constraints	3
Objective Function	-47.76109086	Max Abs Gradient Element	1.8637498E-6
Lambda	0	Actual Over Pred Change	0
Radius	0.0024776027

GCONV convergence criterion satisfied.

Output 4.8.2 lists the optimal parameters with the gradient.

Output 4.8.2: Optimization Results