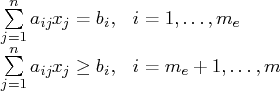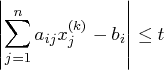| The NLP Procedure |
Active Set Methods
The parameter vector ![]() may be subject to
a set of
may be subject to
a set of ![]() linear equality and inequality constraints:
linear equality and inequality constraints:
The ![]() linear constraints define a feasible region
linear constraints define a feasible region ![]() in
in ![]() that must contain the point
that must contain the point ![]() that minimizes
the problem. If the feasible region
that minimizes
the problem. If the feasible region ![]() is empty, no
solution to the optimization problem exists.
is empty, no
solution to the optimization problem exists.
All optimization techniques in PROC NLP (except those processing
nonlinear constraints) are active set methods. The iteration
starts with a feasible point ![]() , which either is
provided by the user or can be computed by the Schittkowski and Stoer (1979)
algorithm implemented in PROC NLP. The algorithm then moves from
one feasible point
, which either is
provided by the user or can be computed by the Schittkowski and Stoer (1979)
algorithm implemented in PROC NLP. The algorithm then moves from
one feasible point ![]() to a better feasible point
to a better feasible point ![]() along a feasible search direction
along a feasible search direction ![]() :
:
Theoretically, the path of points ![]() never leaves the
feasible region
never leaves the
feasible region ![]() of the optimization problem, but it
can hit its boundaries. The active set
of the optimization problem, but it
can hit its boundaries. The active set ![]() of point
of point
![]() is defined as the index set of all linear equality
constraints and those inequality constraints that are satisfied
at
is defined as the index set of all linear equality
constraints and those inequality constraints that are satisfied
at ![]() . If no constraint is active for
. If no constraint is active for
![]() , the point is located in the interior of
, the point is located in the interior of
![]() , and the active set
, and the active set ![]() is
empty. If the point
is
empty. If the point ![]() in iteration
in iteration ![]() hits the boundary
of inequality constraint
hits the boundary
of inequality constraint ![]() , this constraint
, this constraint ![]() becomes active
and is added to
becomes active
and is added to ![]() . Each equality or active inequality
constraint reduces the dimension
(degrees of freedom) of the optimization problem.
. Each equality or active inequality
constraint reduces the dimension
(degrees of freedom) of the optimization problem.
In practice, the active constraints can be satisfied only with
finite precision. The LCEPSILON=![]() option
specifies the range for
active and violated linear constraints.
If the point
option
specifies the range for
active and violated linear constraints.
If the point ![]() satisfies the condition
satisfies the condition
If you cannot expect an improvement in the value of the objective
function by moving from an active constraint back into the interior
of the feasible region, you use this inequality constraint as an
equality constraint in the next iteration. That means the active
set ![]() still contains the constraint
still contains the constraint ![]() . Otherwise
you release the active inequality constraint and increase the dimension
of the optimization problem in the next iteration.
. Otherwise
you release the active inequality constraint and increase the dimension
of the optimization problem in the next iteration.
A serious numerical problem can arise when some of the active constraints
become (nearly) linearly dependent. Linearly dependent equality constraints
are removed before entering the optimization. You can use the
LCSINGULAR=
option to specify a criterion ![]() used in the update of the QR
decomposition that decides whether an active constraint is linearly
dependent relative to a set of other active constraints.
used in the update of the QR
decomposition that decides whether an active constraint is linearly
dependent relative to a set of other active constraints.
If the final parameter set ![]() is subjected to
is subjected to ![]() linear
equality or active inequality constraints, the QR decomposition of
the
linear
equality or active inequality constraints, the QR decomposition of
the ![]() matrix
matrix ![]() of the linear constraints
is computed by
of the linear constraints
is computed by ![]() , where
, where ![]() is an
is an ![]() orthogonal matrix and
orthogonal matrix and ![]() is an
is an ![]() upper triangular
matrix. The
upper triangular
matrix. The ![]() columns of matrix
columns of matrix ![]() can be separated into two
matrices,
can be separated into two
matrices, ![]() , where
, where ![]() contains the first
contains the first ![]() orthogonal
columns of
orthogonal
columns of ![]() and
and ![]() contains the last
contains the last ![]() orthogonal columns of
orthogonal columns of ![]() .
The
.
The ![]() column-orthogonal matrix
column-orthogonal matrix ![]() is also called
the nullspace matrix of the active linear constraints
is also called
the nullspace matrix of the active linear constraints ![]() .
The
.
The ![]() columns of the
columns of the ![]() matrix
matrix
![]() form a basis orthogonal to the rows of the
form a basis orthogonal to the rows of the ![]() matrix
matrix ![]() .
.
At the end of the iteration process, the PROC NLP can display the projected gradient
Those elements of the ![]() vector of first-order estimates
of Lagrange multipliers
vector of first-order estimates
of Lagrange multipliers
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.