| The NETFLOW Procedure |
RESET Statement
- RESET options ;
- SET options ;
The RESET statement is used to change options after PROC NETFLOW has started execution. Any of the following options can appear in the PROC NETFLOW statement.
Another name for the RESET statement is SET. You can use RESET when you are resetting options and SET when you are setting options for the first time.
The following options fall roughly into five categories:
- output data set specifications
- options that indicate conditions under which optimization is to be halted temporarily, giving you an opportunity to use PROC NETFLOW interactively
- options that control aspects of the operation of the network primal simplex optimization
- options that control the pricing strategies of the network simplex optimizer
- miscellaneous options
If you want to examine the setting of any options, use the SHOW statement. If you are interested in looking at only those options that fall into a particular category, the SHOW statement has options that enable you to do this.
The execution of PROC NETFLOW has three stages. In stage zero the problem data are read from the NODEDATA=, ARCDATA=, and CONDATA= data sets. If a warm start is not available, an initial basic feasible solution is found. Some options of the PROC NETFLOW statement control what occurs in stage zero. By the time the first RESET statement is processed, stage zero has already been completed.
In the first stage, an optimal solution to the network flow problem neglecting any side constraints is found. The primal and dual solutions for this relaxed problem can be saved in the ARCOUT= data set and the NODEOUT= data set, respectively.
In the second stage, the side constraints are examined and some initializations occur. Some preliminary work is also needed to commence optimization that considers the constraints. An optimal solution to the network flow problem with side constraints is found. The primal and dual solutions for this side-constrained problem are saved in the CONOUT= data set and the DUALOUT= data set, respectively.
Many options in the RESET statement have the same name except that they have as a suffix the numeral 1 or 2. Such options have much the same purpose, but option1 controls what occurs during the first stage when optimizing the network neglecting any side constraints and option2 controls what occurs in the second stage when PROC NETFLOW is performing constrained optimization.
Some options can be turned off by the option prefixed by the word NO. For example, FEASIBLEPAUSE1 may have been specified in a RESET statement and in a later RESET statement, you can specify NOFEASIBLEPAUSE1. In a later RESET statement, you can respecify FEASIBLEPAUSE1 and, in this way, toggle this option.
The options available with the RESET statement are summarized by purpose in the following table.
Table 5.3: Functional Summary, RESET Statement
| Description | Statement | Option |
| Output Data Set Options: | ||
| unconstrained primal solution data set | RESET | ARCOUT= |
| unconstrained dual solution data set | RESET | NODEOUT= |
| constrained primal solution data set | RESET | CONOUT= |
| constrained dual solution data set | RESET | DUALOUT= |
| Simplex Options: | ||
| use big-M instead of two-phase method, stage 1 | RESET | BIGM1 |
| use Big-M instead of two-phase method, stage 2 | RESET | BIGM2 |
| anti-cycling option | RESET | CYCLEMULT1= |
| interchange first nonkey with leaving key arc | RESET | INTFIRST |
| controls working basis matrix inversions | RESET | INVFREQ= |
| maximum number of L row operations allowed before refactorization | RESET | MAXL= |
| maximum number of LU factor column updates | RESET | MAXLUUPDATES= |
| anti-cycling option | RESET | MINBLOCK1= |
| use first eligible leaving variable, stage 1 | RESET | LRATIO1 |
| use first eligible leaving variable, stage 2 | RESET | LRATIO2 |
| negates INTFIRST | RESET | NOINTFIRST |
| negates LRATIO1 | RESET | NOLRATIO1 |
| negates LRATIO2 | RESET | NOLRATIO2 |
| negates PERTURB1 | RESET | NOPERTURB1 |
| anti-cycling option | RESET | PERTURB1 |
| controls working basis matrix refactorization | RESET | REFACTFREQ= |
| use two-phase instead of big-M method, stage 1 | RESET | TWOPHASE1 |
| use two-phase instead of big-M method, stage 2 | RESET | TWOPHASE2 |
| pivot element selection parameter | RESET | U= |
| zero tolerance, stage 1 | RESET | ZERO1= |
| zero tolerance, stage 2 | RESET | ZERO2= |
| zero tolerance, real number comparisons | RESET | ZEROTOL= |
| Pricing Options: | ||
| frequency of dual value calculation | RESET | DUALFREQ= |
| pricing strategy, stage 1 | RESET | PRICETYPE1= |
| pricing strategy, stage 2 | RESET | PRICETYPE2= |
| used when P1SCAN=PARTIAL | RESET | P1NPARTIAL= |
| controls search for entering candidate, stage 1 | RESET | P1SCAN= |
| used when P2SCAN=PARTIAL | RESET | P2NPARTIAL= |
| controls search for entering candidate, stage 2 | RESET | P2SCAN= |
| initial queue size, stage 1 | RESET | QSIZE1= |
| initial queue size, stage 2 | RESET | QSIZE2= |
| used when Q1FILLSCAN=PARTIAL | RESET | Q1FILLNPARTIAL= |
| controls scan when filling queue, stage 1 | RESET | Q1FILLSCAN= |
| used when Q2FILLSCAN=PARTIAL | RESET | Q2FILLNPARTIAL= |
| controls scan when filling queue, stage 2 | RESET | Q2FILLSCAN= |
| queue size reduction factor, stage 1 | RESET | REDUCEQSIZE1= |
| queue size reduction factor, stage 2 | RESET | REDUCEQSIZE2= |
| frequency of refreshing queue, stage 1 | RESET | REFRESHQ1= |
| frequency of refreshing queue, stage 2 | RESET | REFRESHQ2= |
| Optimization Termination Options: | ||
| pause after stage 1; don't start stage 2 | RESET | ENDPAUSE1 |
| pause when feasible, stage 1 | RESET | FEASIBLEPAUSE1 |
| pause when feasible, stage 2 | RESET | FEASIBLEPAUSE2 |
| maximum number of iterations, stage 1 | RESET | MAXIT1= |
| maximum number of iterations, stage 2 | RESET | MAXIT2= |
| negates ENDPAUSE1 | RESET | NOENDPAUSE1 |
| negates FEASIBLEPAUSE1 | RESET | NOFEASIBLEPAUSE1 |
| negates FEASIBLEPAUSE2 | RESET | NOFEASIBLEPAUSE2 |
| pause every PAUSE1 iterations, stage 1 | RESET | PAUSE1= |
| pause every PAUSE2 iterations, stage 2 | RESET | PAUSE2= |
| Interior Point Algorithm Options: | ||
| factorization method | RESET | FACT_METHOD= |
| allowed amount of dual infeasibility | RESET | TOLDINF= |
| allowed amount of primal infeasibility | RESET | TOLPINF= |
| allowed total amount of dual infeasibility | RESET | TOLTOTDINF= |
| allowed total amount of primal infeasibility | RESET | TOLTOTPINF= |
| cut-off tolerance for Cholesky factorization | RESET | CHOLTINYTOL= |
| density threshold for Cholesky processing | RESET | DENSETHR= |
| step-length multiplier | RESET | PDSTEPMULT= |
| preprocessing type | RESET | PRSLTYPE= |
| print optimization progress on SAS log | RESET | PRINTLEVEL2= |
| Interior Point Stopping Criteria Options: | ||
| maximum number of interior point iterations | RESET | MAXITERB= |
| primal-dual (duality) gap tolerance | RESET | PDGAPTOL= |
| stop because of complementarity | RESET | STOP_C= |
| stop because of duality gap | RESET | STOP_DG= |
| stop because of | RESET | STOP_IB= |
| stop because of | RESET | STOP_IC= |
| stop because of | RESET | STOP_ID= |
| stop because of complementarity | RESET | AND_STOP_C= |
| stop because of duality gap | RESET | AND_STOP_DG= |
| stop because of | RESET | AND_STOP_IB= |
| stop because of | RESET | AND_STOP_IC= |
| stop because of | RESET | AND_STOP_ID= |
| stop because of complementarity | RESET | KEEPGOING_C= |
| stop because of duality gap | RESET | KEEPGOING_DG= |
| stop because of | RESET | KEEPGOING_IB= |
| stop because of | RESET | KEEPGOING_IC= |
| stop because of | RESET | KEEPGOING_ID= |
| stop because of complementarity | RESET | AND_KEEPGOING_C= |
| stop because of duality gap | RESET | AND_KEEPGOING_DG= |
| stop because of | RESET | AND_KEEPGOING_IB= |
| stop because of | RESET | AND_KEEPGOING_IC= |
| stop because of | RESET | AND_KEEPGOING_ID= |
| Miscellaneous Options: | ||
| output complete basis information to ARCOUT= and NODEOUT= data sets | RESET | FUTURE1 |
| output complete basis information to CONOUT= and DUALOUT= data sets | RESET | FUTURE2 |
| turn off infeasibility or optimality flags | RESET | MOREOPT |
| negates FUTURE1 | RESET | NOFUTURE1 |
| negates FUTURE2 | RESET | NOFUTURE2 |
| negates SCRATCH | RESET | NOSCRATCH |
| negates ZTOL1 | RESET | NOZTOL1 |
| negates ZTOL2 | RESET | NOZTOL2 |
| write optimization time to SAS log | RESET | OPTIM_TIMER |
| no stage 1 optimization; do stage 2 optimization | RESET | SCRATCH |
| suppress similar SAS log messages | RESET | VERBOSE= |
| use zero tolerance, stage 1 | RESET | ZTOL1 |
| use zero tolerance, stage 2 | RESET | ZTOL2 |
Output Data Set Specifications
In a RESET statement, you can specify an ARCOUT= data set, a NODEOUT= data set, a CONOUT= data set, or a DUALOUT= data set. You are advised to specify these output data sets early because if you make a syntax error when using PROC NETFLOW interactively or, for some other reason, PROC NETFLOW encounters or does something unexpected, these data sets will contain information about the solution that was reached. If you had specified the FUTURE1 or FUTURE2 option in a RESET statement, PROC NETFLOW may be able to resume optimization in a subsequent run.You can turn off these current output data set specifications by specifying ARCOUT=NULL, NODEOUT=NULL, CONOUT=NULL, or DUALOUT=NULL.
If PROC NETFLOW is outputting observations to an output data set and you want this to stop, press the keys used to stop SAS procedures. PROC NETFLOW waits, if necessary, and then executes the next statement.
- ARCOUT=SAS-data-set
- AOUT=SAS-data-set
-
names the output data set that receives all information concerning
arc and nonarc variables, including flows and other information concerning the current solution and
the supply and demand information.
The current solution is the latest solution found by the
optimizer when the optimization
neglecting side constraints is halted or the unconstrained optimum
is reached.
You can specify an ARCOUT= data set in any RESET statement before the unconstrained optimum is found (even at commencement). Once the unconstrained optimum has been reached, use the SAVE statement to produce observations in an ARCOUT= data set. Once optimization that considers constraints starts, you will be unable to obtain an ARCOUT= data set. Instead, use a CONOUT= data set to get the current solution. See the section "ARCOUT= and CONOUT= Data Sets" for more information. - CONOUT=SAS-data-set
- COUT=SAS-data-set
-
names the output data set that contains the primal solution
obtained after optimization considering
side constraints reaches the optimal solution.
You can specify a CONOUT= data set in any RESET
statement before the constrained optimum is found (even at
commencement or while optimizing neglecting constraints).
Once the constrained optimum has been reached, or during stage 2
optimization,
use the SAVE statement
to produce observations in a CONOUT= data set.
See the section "ARCOUT= and CONOUT= Data Sets" for more information.
- DUALOUT=SAS-data-set
- DOUT=SAS-data-set
-
names the output data set that contains the dual solution
obtained after doing optimization that considers
side constraints reaches the optimal solution.
You can specify a DUALOUT= data set in any RESET
statement before the constrained optimum is found (even at
commencement or while optimizing neglecting constraints).
Once the constrained optimum has been reached, or during stage
2 optimization,
use the SAVE statement
to produce observations in a DUALOUT= data set.
See the section "NODEOUT= and DUALOUT= Data Sets" for more information.
- NODEOUT=SAS-data-set
- NOUT=SAS-data-set
-
names the output data set that receives all information about nodes
(supply/demand and nodal dual variable values) and other information
concerning the unconstrained optimal solution.
You can specify a NODEOUT= data set in any RESET statement before the unconstrained optimum is found (even at commencement). Once the unconstrained optimum has been reached, or during stage 1 optimization, use the SAVE statement to produce observations in a NODEOUT= data set. Once optimization that considers constraints starts, you will not be able to obtain a NODEOUT= data set. Instead use a DUALOUT= data set to get the current solution. See the section "NODEOUT= and DUALOUT= Data Sets" for more information.
Options to Halt Optimization
The following options indicate conditions when optimization is to be halted. You then have a chance to use PROC NETFLOW interactively. If the NETFLOW procedure is optimizing and you want optimization to halt immediately, press the CTRL-BREAK key combination used to stop SAS procedures. Doing this is equivalent to PROC NETFLOW finding that some prespecified condition of the current solution under which optimization should stop has occurred.If optimization does halt, you may need to change the conditions for when optimization should stop again. For example, if the number of iterations exceeded MAXIT2, use the RESET statement to specify a larger value for the MAXIT2= option before the next RUN statement. Otherwise, PROC NETFLOW will immediately find that the number of iterations still exceeds MAXIT2 and halt without doing any additional optimization.
- ENDPAUSE1
-
indicates that PROC NETFLOW will pause
after the unconstrained optimal solution has been obtained and
information about this solution has been output to the current
ARCOUT= data set, NODEOUT= data set, or both.
The procedure then executes the
next statement, or waits if no subsequent statement has been
specified.
- FEASIBLEPAUSE1
- FP1
-
indicates that unconstrained optimization should stop once a
feasible solution is reached. PROC NETFLOW checks for feasibility
every 10 iterations. A solution is feasible if there are no
artificial arcs having nonzero flow assigned to be conveyed
through them.
The presence of
artificial arcs with nonzero flows means that the current solution
does not satisfy all the nodal flow
conservation constraints implicit in network problems.
- MAXIT1=m
-
specifies the maximum number of primal simplex iterations PROC NETFLOW
is to perform in stage 1.
The default value for the MAXIT1= option is 1000.
If MAXIT1=m iterations are performed and you want to
continue unconstrained optimization, reset MAXIT1= to
a number larger than the
number of iterations already performed
and issue another RUN statement.
- NOENDPAUSE1
- NOEP1
-
negates the ENDPAUSE1 option.
- NOFEASIBLEPAUSE1
- NOFP1
-
negates the FEASIBLEPAUSE1 option.
- PAUSE1=p
-
indicates that PROC NETFLOW will halt unconstrained optimization and
pause when the
remainder of the number of stage 1 iterations divided by
the value of the PAUSE1= option is zero.
If present, the next statement is executed; if not,
the procedure waits for the next statement to be specified.
The default value for PAUSE1= is 999999.
- FEASIBLEPAUSE2
- FP2
- NOFEASIBLEPAUSE2
- NOFP2
- PAUSE2=p
- MAXIT2=m
-
are the stage 2 constrained optimization counterparts of the
options described previously and having as a suffix the numeral 1.
Options Controlling the Network Simplex Optimization
- BIGM1
- NOTWOPHASE1
- TWOPHASE1
- NOBIGM1
-
BIGM1 indicates that the "big-M" approach to optimization is
used. Artificial variables are treated like real arcs, slacks,
surpluses and nonarc variables. Artificials have very expensive
costs. BIGM1 is the default.
TWOPHASE1 indicates that the two-phase approach is used instead of the big-M approach. At first, artificial variables are the only variables to have nonzero objective function coefficients. An artificial variable's objective function coefficient is temporarily set to 1 and PROC NETFLOW minimizes. When all artificial variables have zero value, PROC NETFLOW has found a feasible solution, and phase 2 commences. Arcs and nonarc variables have their real costs and objective function coefficients.
Before all artificial variables are driven to have zero value, you can toggle between the big-M and the two-phase approaches by specifying BIGM1 or TWOPHASE1 in a RESET statement. The option NOTWOPHASE1 is synonymous with BIGM1, and NOBIGM1 is synonymous with TWOPHASE1. - CYCLEMULT1=c
- MINBLOCK1=m
- NOPERTURB1
- PERTURB1
-
In an effort to reduce the number of iterations performed when the
problem is highly degenerate, PROC NETFLOW has in stage 1 optimization
adopted an algorithm outlined in Ryan and Osborne (1988).
If the number of consecutive degenerate pivots (those with no progress toward the optimum) performed equals the value of the CYCLEMULT1= option times the number of nodes, the arcs that were "blocking" (can leave the basis) are added to a list. In subsequent iterations, of the arcs that now can leave the basis, the one chosen to leave is an arc on the list of arcs that could have left in the previous iteration. In other words, perference is given to arcs that "block" many iterations. After several iterations, the list is cleared.
If the number of blocking arcs is less than the value of the MINBLOCK1= option, a list is not kept. Otherwise, if PERTURB1 is specified, the arc flows are perturbed by a random quantity, so that arcs on the list that block subsequent iterations are chosen to leave the basis randomly. Although perturbation often pays off, it is computationally expensive. Periodically, PROC NETFLOW has to clear out the lists and un-perturb the solution. You can specify NOPERTURB1 to prevent perturbation.
Defaults are CYCLEMULT1=0.15, MINBLOCK1=2, and NOPERTURB1. - LRATIO1
-
specifies the type of ratio test to use in determining
which arc leaves the basis in stage 1.
In some iterations, more than one arc is eligible to leave the basis.
Of those arcs that can leave the
basis, the leaving arc is the first encountered by the algorithm
if the LRATIO1 option is specified.
Specifying the LRATIO1 option can decrease the chance of cycling but can
increase solution times.
The alternative to the LRATIO1 option is the NOLRATIO1 option, which
is the default.
- LRATIO2
-
specifies the type of ratio test to use in determining
what leaves the basis in stage 2.
In some iterations, more than one arc, constraint slack, surplus,
or nonarc variable is eligible to leave the basis.
If the LRATIO2 option is specified, the leaving arc, constraint slack, surplus,
or nonarc variable is the one that is eligible to leave the
basis first encountered by the algorithm.
Specifying the LRATIO2 option can decrease the chance of cycling but can
increase solution times.
The alternative to the LRATIO2 option is the NOLRATIO2 option, which
is the default.
- NOLRATIO1
-
specifies the type of ratio test to use in determining
which arc leaves the basis in stage 1.
If the NOLRATIO1 option is specified, of those arcs
that can leave the
basis, the leaving arc
has the minimum (maximum) cost if the leaving
arc is to be nonbasic with flow capacity equal to its
capacity (lower flow bound).
If more than one
possible leaving arc has the minimum (maximum) cost, the
first such arc encountered is chosen.
Specifying the NOLRATIO1 option can decrease solution times, but can
increase the chance of cycling.
The alternative to the NOLRATIO1 option is the LRATIO1 option.
The NOLRATIO1 option is the default.
- NOLRATIO2
-
specifies the type of ratio test to use in determining
which arc leaves the basis in stage 2.
If the NOLRATIO2 option is specified, the leaving arc, constraint slack, surplus,
or nonarc variable is the one eligible to leave the
basis with the minimum (maximum) cost or objective function coefficient
if the leaving
arc, constraint slack or nonarc variable is to be nonbasic with
flow or value equal to its capacity or upper value bound
(lower flow or value bound), respectively.
If several possible leaving arcs,
constraint slacks, surpluses, or nonarc variables
have the minimum (maximum) cost or objective function coefficient,
then the first encountered is chosen.
Specifying the NOLRATIO2 option can decrease solution times, but
can increase the chance of cycling.
The alternative to the NOLRATIO2 option is the LRATIO2 option.
The NOLRATIO2 option is the default.
Options Applicable to Constrained Optimization
The INVFREQ= option is relevant only if INVD_2D is specified in the PROC NETFLOW statement; that is, the inverse of the working basis matrix is being stored and processed as a two-dimensional array. The REFACTFREQ=, U=, MAXLUUPDATES=, and MAXL= options are relevant if the INVD_2D option is not specified in the PROC NETFLOW statement; that is, if the working basis matrix is LU factored.- BIGM2
- NOTWOPHASE2
- TWOPHASE2
- NOBIGM2
-
are the stage 2 constrained optimization counterparts of the
options BIGM1,
NOTWOPHASE1, TWOPHASE1, and NOBIGM1.
The TWOPHASE2 option is often better than the BIGM2 option when the problem has many side constraints. - INVFREQ=n
-
recalculates the working basis matrix
inverse whenever n iterations have been performed where n
is the value of the INVFREQ= option. Although a relatively expensive task,
it is prudent to do as roundoff errors
accumulate, especially affecting the elements of this matrix inverse.
The default is INVFREQ=50.
The INVFREQ= option should be used only if the INVD_2D option is specified in
the PROC NETFLOW statement.
- INTFIRST
-
In some iterations, it is found that what must
leave the basis is an arc that is part of the spanning tree
representation of the network part of the basis
(called a key arc).
It is
necessary to interchange another basic arc not part of the tree
(called a nonkey arc)
with the tree arc that leaves to permit the basis update
to be performed efficiently.
Specifying the INTFIRST option indicates that of the nonkey arcs eligible to be
swapped with the leaving key arc, the one chosen to do so is the first
encountered by the algorithm.
If the INTFIRST option is not
specified, all such arcs are examined and the one with the best
cost is chosen.
The terms key and nonkey are used because the algorithm used by PROC NETFLOW for network optimization considering side constraints (GUB-based, Primal Partitioning, or Factorization) is a variant of an algorithm originally developed to solve linear programming problems with generalized upper bounding constraints. The terms key and nonkey were coined then. The STATUS SAS variable in the ARCOUT= and CONOUT= data sets and the STATUS column in tables produced when PRINT statements are processed indicate whether basic arcs are key or nonkey. Basic nonarc variables are always nonkey. - MAXL=m
-
If the working basis matrix is LU factored,
U is an upper triangular
matrix and L is a lower triangular matrix corresponding to
a sequence of
elementary matrix
row operations required to change the working basis
matrix into U.
L and U enable
substitution techniques to be used to solve the
linear systems of the simplex algorithm.
Among other things, the LU processing
strives to keep the number of
L elementary matrix row operation matrices small.
A buildup in the number of these could indicate that fill-in
is becoming excessive and the computations involving
L and U will
be hampered.
Refactorization should be performed to restore
U sparsity and reduce L information.
When the number of L matrix
row operations exceeds the value of the MAXL= option, a
refactorization is done rather than one or more updates.
The default value for MAXL= is 10 times the number of side constraints.
The MAXL= option should not be used if INVD_2D is specified in
the PROC NETFLOW statement.
- MAXLUUPDATES=m
- MLUU=m
-
In some iterations, PROC NETFLOW must either perform a series of single
column updates or a complete refactorization of the working basis matrix.
More than one column of the working basis
matrix must change before the next simplex iteration can begin.
The single column updates can often be done faster than
a complete refactorization,
especially if few updates are necessary, the working basis
matrix is sparse, or a refactorization has been performed recently.
If the number of columns that must change is less than
the value specified in the MAXLUUPDATES= option,
the updates are attempted; otherwise, a refactorization is done.
Refactorization also occurs
if the sum of the number of columns that must be changed and
the number of LU updates done since the last refactorization
exceeds the value of the REFACTFREQ= option.
The MAXLUUPDATES= option should not be used if the INVD_2D option is specified in
the PROC NETFLOW statement.
In some iterations, a series of single column updates are not able to complete the changes required for a working basis matrix because, ideally, all columns should change at once. If the update cannot be completed, PROC NETFLOW performs a refactorization. The default value is 5. - NOINTFIRST
-
indicates that of the arcs eligible to be
swapped with the leaving arc, the one chosen to do so has the best cost.
See the INTFIRST option.
- REFACTFREQ=r
- RFF=r
-
specifies the maximum number of
L and U updates between
refactorization of the working basis matrix
to reinitialize LU factors.
In most iterations, one or several
Bartels-Golub updates can be performed.
An update is performed
more quickly than a complete refactorization. However, after
a series of updates, the sparsity of the U factor is degraded.
A refactorization is necessary to regain sparsity and to make
subsequent computations and updates more efficient.
The default value is 50.
The REFACTFREQ= option should not be used if INVD_2D is specified in
the PROC NETFLOW statement.
- U=u
-
controls the choice of pivot
during LU decomposition or Bartels-Golub update.
When searching for a pivot, any element less than the value of the U= option times
the
largest element in its matrix row is excluded, or matrix
rows are interchanged to improve numerical stability.
The U= option should have values on or between ZERO2 and 1.0.
Decreasing the value of the
U= option biases the algorithm toward maintaining
sparsity at the expense of numerical stability and vice-versa.
Reid (1975) suggests that the value of 0.01 is acceptable and this
is the default for the U= option.
This option should not be used if INVD_2D is specified in
the PROC NETFLOW statement.
Pricing Strategy Options
There are three main types of pricing strategies:- PRICETYPE
 =NOQ
=NOQ
- PRICETYPE
 =BLAND
=BLAND
- PRICETYPE
 =Q
=Q
The one that usually performs better than the others is PRICETYPE
Because the pricing strategy takes a lot of computational time, you should experiment with the following options to find the optimum specification. These options influence how the pricing step of the simplex iteration is performed. See the section "Pricing Strategies" for further information.
- PRICETYPE
 =BLAND or PTYPE
=BLAND or PTYPE =BLAND
=BLAND
- PRICETYPE
 =NOQ or PTYPE
=NOQ or PTYPE =NOQ
=NOQ
- P
 SCAN=BEST
SCAN=BEST
- P
 SCAN=FIRST
SCAN=FIRST
- P
 SCAN=PARTIAL and P
SCAN=PARTIAL and P NPARTIAL=p
NPARTIAL=p
- P
- PRICETYPE
 =Q or PTYPE
=Q or PTYPE =Q
=Q
QSIZE =q or Q
=q or Q =q
=q
REFRESHQ =r
=r
REDUCEQSIZE =r
=r
REDUCEQ =r
=r
- P
 SCAN=BEST
SCAN=BEST
- P
 SCAN=FIRST
SCAN=FIRST
- P
 SCAN=PARTIAL and P
SCAN=PARTIAL and P NPARTIAL=p
NPARTIAL=p
- Q
 FILLSCAN=BEST
FILLSCAN=BEST
- Q
 FILLSCAN=FIRST
FILLSCAN=FIRST
- Q
 FILLSCAN=PARTIAL and Q
FILLSCAN=PARTIAL and Q FILLNPARTIAL=q
FILLNPARTIAL=q
- P
For stage 2 optimization, you can specify P2SCAN=ANY, which is used in conjunction with the DUALFREQ= option.
Miscellaneous Options
- FUTURE1
-
signals that PROC NETFLOW must output extra observations to
the NODEOUT= and ARCOUT= data sets.
These observations contain information about the
solution
found by doing optimization
neglecting any side constraints.
These two data sets then can
be used as the NODEDATA=
and ARCDATA= data sets, respectively,
in subsequent
PROC NETFLOW runs with the WARM option specified.
See the section "Warm Starts".
- FUTURE2
-
signals that PROC NETFLOW must output extra observations to
the DUALOUT= and CONOUT= data sets.
These observations contain information about the
solution
found by optimization that considers side constraints.
These two data sets can then
be used as the NODEDATA= data set (also called the DUALIN= data set)
and the ARCDATA= data sets, respectively,
in subsequent
PROC NETFLOW runs with the WARM option specified.
See the section "Warm Starts".
- MOREOPT
-
The MOREOPT option turns off all optimality and infeasibility flags that may
have been raised. Unless this is done, PROC NETFLOW will not do any
optimization when a RUN statement is specified.
If PROC NETFLOW determines that the problem is infeasible, it will not do any more optimization unless you specify MOREOPT in a RESET statement. At the same time, you can try resetting options (particularly zero tolerances) in the hope that the infeasibility was raised incorrectly.
Consider the following example:proc netflow nodedata=noded /* supply and demand data */ arcdata=arcd1 /* the arc descriptions */ condata=cond1 /* the side constraints */ conout=solution; /* output the solution */ run; /* Netflow states that the problem is infeasible. */ /* You suspect that the zero tolerance is too large */ reset zero2=1.0e-10 moreopt; run; /* Netflow will attempt more optimization. */ /* After this, if it reports that the problem is */ /* infeasible, the problem really might be infeasible */
If PROC NETFLOW finds an optimal solution, you might want to do additional optimization to confirm that an optimum has really been reached. Specify the MOREOPT option in a RESET statement. Reset options, but in this case tighten zero tolerances. - NOFUTURE1
-
negates the FUTURE1 option.
- NOFUTURE2
-
negates the FUTURE2 option.
- NOSCRATCH
-
negates the SCRATCH option.
- NOZTOL1
-
indicates that the majority of tests for roundoff error should
not be done.
Specifying the NOZTOL1 option
and obtaining the same optimal solution as when the NOZTOL1
option is not specified
in the PROC NETFLOW statement
(or the ZTOL1 option is specified), verifies that the zero tolerances
were not too high.
Roundoff error checks that are critical to the successful
functioning of PROC NETFLOW
and any related readjustments are always done.
- NOZTOL2
-
indicates that the majority of tests for roundoff error
are not to be done during an
optimization that considers side constraints.
The reasons for specifying the NOZTOL2 option are the same as those for
specifying the NOZTOL1 option for stage 1 optimization (see the NOZTOL1 option).
- OPTIM_TIMER
-
indicates that the procedure is to issue a message to the SAS log
giving the CPU time spent doing optimization. This includes the time
spent preprocessing, performing optimization, and postprocessing.
Not counted in that time is the rest of the procedure execution, which
includes reading the data and creating output SAS data sets.
The time spent optimizing can be small compared to the total CPU time used by the procedure. This is especially true when the problem is quite small (e.g., fewer than 10,000 variables). - SCRATCH
-
specifies that you do not want PROC
NETFLOW to enter or continue stage 1 of
the algorithm.
Rather than specify RESET SCRATCH, you can use
the CONOPT statement.
- VERBOSE=v
-
limits the number of similar messages that are displayed on the SAS log.
For example, when reading the ARCDATA= data set, PROC NETFLOW might have cause to issue the following message many times:ERROR: The HEAD list variable value in obs i in ARCDATA is missing and the TAIL list variable value of this obs is nonmissing. This is an incomplete arc specification.If there are many observations that have this fault, messages that are similar are issued for only the first VERBOSE= such observations. After the ARCDATA= data set has been read, PROC NETFLOW will issue the messageNOTE: More messages similar to the ones immediately above could have been issued but were suppressed as VERBOSE=v.
If observations in the ARCDATA= data set have this error, PROC NETFLOW stops and you have to fix the data. Imagine that this error is only a warning and PROC NETFLOW proceeded to other operations such as reading the CONDATA= data set. If PROC NETFLOW finds there are numerous errors when reading that data set, the number of messages issued to the SAS log are also limited by the VERBOSE= option.
If you have a problem with a large number of side constraints and for some reason you stop stage 2 optimization early, PROC NETFLOW indicates that constraints are violated by the current solution. Specifying VERBOSE=v allows at most v violated constraints to be written to the log. If there are more, these are not displayed.
When PROC NETFLOW finishes and messages have been suppressed, the messageNOTE: To see all messages, specify VERBOSE=vmin.
is issued. The value of vmin is the smallest value that should be specified for the VERBOSE= option so that all messages are displayed if PROC NETFLOW is run again with the same data and everything else (except the VERBOSE= option) unchanged. No messages are suppressed.
The default value for the VERBOSE= option is 12. - ZERO1=z
- Z1=z
-
specifies the zero tolerance level in stage 1.
If the NOZTOL1 option is not specified,
values within z of zero are set to 0.0,
where z is the value of the ZERO1= option.
Flows close to the lower flow bound or capacity of arcs are
reassigned those exact values.
Two values are deemed to be close if one is within
z of the other.
The default value for the ZERO1= option is 0.000001.
Any value specified for the ZERO1= option that is < 0.0 or > 0.0001 is invalid.
- ZERO2=z
- Z2=z
-
specifies the zero tolerance level in stage 2.
If the NOZTOL2 option is not specified,
values within z of zero are set to 0.0,
where z is the value of the ZERO2= option.
Flows close to the lower flow bound or capacity of arcs are
reassigned those exact values.
If there are nonarc variables,
values close to the lower or upper value bound of nonarc variables are
reassigned those exact values.
Two values are deemed to be close if one is within z
of the other.
The default value for the ZERO2= option is 0.000001.
Any value specified for the ZERO2= option that is < 0.0 or > 0.0001 is invalid.
- ZEROTOL=z
-
specifies the zero tolerance used when PROC NETFLOW must compare
any real number with another real number, or zero.
For example, if
 and
and 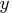 are real numbers, then for
are real numbers, then for  to be
considered greater than
to be
considered greater than 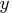 ,
,  must be at least
must be at least 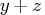 .
The ZEROTOL= option is used throughout any PROC NETFLOW run.
.
The ZEROTOL= option is used throughout any PROC NETFLOW run.
ZEROTOL=z controls the way PROC NETFLOW performs all double precision comparisons; that is, whether a double precision number is equal to, not equal to, greater than (or equal to), or less than (or equal to) zero or some other double precision number. A double precision number is deemed to be the same as another such value if the absolute difference between them is less than or equal to the value of the ZEROTOL= option.
The default value for the ZEROTOL= option is 1.0E-14. You can specify the ZEROTOL= option in the NETFLOW or RESET statement. Valid values for the ZEROTOL= option must be > 0.0 and < 0.0001. Do not specify a value too close to zero as this defeats the purpose of the ZEROTOL= option. Neither should the value be too large, as comparisons might be incorrectly performed.
The ZEROTOL= option is different from the ZERO1= and ZERO2= options in that ZERO1= and ZERO2= options work when determining whether optimality has been reached, whether an entry in the updated column in the ratio test of the simplex method is zero, whether a flow is the same as the arc's capacity or lower bound, or whether the value of a nonarc variable is at a bound. The ZEROTOL= option is used in all other general double precision number comparisons. - ZTOL1
-
indicates that all tests for roundoff error are performed during
stage 1 optimization.
Any alterations are carried out.
The opposite of the ZTOL1 option is the NOZTOL1 option.
- ZTOL2
-
indicates that all tests for roundoff error are performed during
stage 2 optimization.
Any alterations are carried out.
The opposite of the ZTOL2 option is the NOZTOL2 option.
Interior Point Algorithm Options
- FACT_METHOD=f
-
enables you to choose the type of algorithm used to factorize and
solve the main linear systems at each iteration of the
interior point algorithm.
FACT_METHOD=LEFT_LOOKING is new for SAS 9.1.2. It uses algorithms described in George, Liu, and Ng (2001). Left looking is one of the main methods used to perform Cholesky optimization and, along with some recently developed implementation approaches, can be faster and require less memory than other algorithms.
Specify FACT_METHOD=USE_OLD if you want the procedure to use the only factorization available prior to SAS 9.1.2. - TOLDINF=t
- RTOLDINF=t
-
specifies the allowed amount of dual infeasibility.
In the section "Interior Point Algorithmic Details", the vector
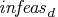 is
defined. If all elements of this vector are
is
defined. If all elements of this vector are 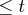 ,
the solution is deemed feasible.
,
the solution is deemed feasible.
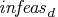 is replaced by a zero vector, making computations faster.
This option is the dual equivalent to the TOLPINF= option.
Valid values for
is replaced by a zero vector, making computations faster.
This option is the dual equivalent to the TOLPINF= option.
Valid values for 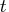 are greater than 1.0E-12. The default is 1.0E-7.
are greater than 1.0E-12. The default is 1.0E-7.
- TOLPINF=t
- RTOLPINF=t
-
specifies the allowed amount of primal infeasibility.
This option is the primal equivalent to the TOLDINF= option.
In the section "Interior Point: Upper Bounds", the vector
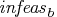 is
defined.
In the section "Interior Point Algorithmic Details", the vector
is
defined.
In the section "Interior Point Algorithmic Details", the vector
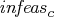 is
defined. If all elements in these vectors are
is
defined. If all elements in these vectors are 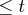 ,
the solution is deemed feasible.
,
the solution is deemed feasible.
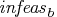 and
and
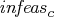 are replaced by zero vectors, making computations faster.
Increasing the value of the TOLPINF= option too much can lead to instability, but a modest increase can give the algorithm added
flexibility and decrease the iteration count.
Valid values for
are replaced by zero vectors, making computations faster.
Increasing the value of the TOLPINF= option too much can lead to instability, but a modest increase can give the algorithm added
flexibility and decrease the iteration count.
Valid values for 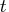 are greater than 1.0E-12.
The default is 1.0E-7.
are greater than 1.0E-12.
The default is 1.0E-7.
- TOLTOTDINF=t
- RTOLTOTDINF=t
-
specifies the allowed total amount of dual infeasibility.
In the section "Interior Point Algorithmic Details", the vector
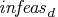 is
defined. If
is
defined. If 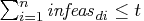 ,
the solution is deemed feasible.
,
the solution is deemed feasible.
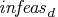 is replaced by a zero vector, making computations faster.
This option is the dual equivalent to the TOLTOTPINF= option.
Valid values for
is replaced by a zero vector, making computations faster.
This option is the dual equivalent to the TOLTOTPINF= option.
Valid values for 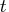 are greater than 1.0E-12. The default is 1.0E-7.
are greater than 1.0E-12. The default is 1.0E-7.
- TOLTOTPINF=t
- RTOLTOTPINF=t
-
specifies the allowed total amount of primal infeasibility.
This option is the primal equivalent to the
TOLTOTDINF= option.
In the section "Interior Point: Upper Bounds", the vector
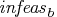 is defined.
In the section "Interior Point Algorithmic Details", the vector
is defined.
In the section "Interior Point Algorithmic Details", the vector
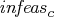 is defined.
If
is defined.
If 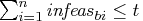 and
and
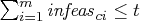 ,
the solution is deemed feasible.
,
the solution is deemed feasible.
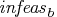 and
and 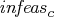 are replaced by zero vectors, making computations faster.
Increasing the value of the TOLTOTPINF= option too much can lead to instability, but a modest increase can give the algorithm added
flexibility and decrease the iteration count.
Valid values for
are replaced by zero vectors, making computations faster.
Increasing the value of the TOLTOTPINF= option too much can lead to instability, but a modest increase can give the algorithm added
flexibility and decrease the iteration count.
Valid values for 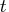 are greater than 1.0E-12. The default is 1.0E-7.
are greater than 1.0E-12. The default is 1.0E-7.
- CHOLTINYTOL=c
- RCHOLTINYTOL=c
-
specifies the cut-off tolerance for Cholesky factorization of the
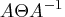 .
If a diagonal value drops below c, the row is essentially
treated as dependent and is ignored in the factorization.
Valid values for c are between 1.0E-30 and 1.0E-6.
The default value is 1.0E-8.
.
If a diagonal value drops below c, the row is essentially
treated as dependent and is ignored in the factorization.
Valid values for c are between 1.0E-30 and 1.0E-6.
The default value is 1.0E-8.
- DENSETHR=d
- RDENSETHR=d
-
specifies the density threshold for Cholesky processing.
When the symbolic factorization
encounters a column of
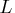 that
has DENSETHR= proportion of nonzeros and the
remaining part of
that
has DENSETHR= proportion of nonzeros and the
remaining part of 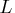 is at least
is at least 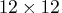 , the remainder of
, the remainder of 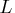 is
treated as dense. In practice, the lower right
part of the Cholesky triangular factor
is
treated as dense. In practice, the lower right
part of the Cholesky triangular factor 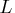 is quite dense and it can be
computationally more efficient to
treat it as 100% dense.
The default value for d is 0.7.
A specification of
is quite dense and it can be
computationally more efficient to
treat it as 100% dense.
The default value for d is 0.7.
A specification of 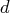
 0.0 causes all dense processing;
0.0 causes all dense processing;
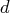
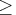 1.0 causes all sparse processing.
1.0 causes all sparse processing.
- PDSTEPMULT=p
- RPDSTEPMULT=p
-
specifies the step-length multiplier.
The maximum feasible step-length chosen by the
Primal-Dual with Predictor-Corrector algorithm is multiplied
by the value of the PDSTEPMULT= option.
This number must be less than 1 to avoid moving beyond the barrier.
An actual step length greater than 1 indicates numerical difficulties.
Valid values for p are between 0.01 and 0.999999.
The default value is 0.99995.
In the section "Interior Point Algorithmic Details", the solution of the next iteration is obtained by moving along a direction from the current iteration's solution:
where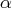 is the maximum feasible step-length chosen by the interior
point algorithm. If
is the maximum feasible step-length chosen by the interior
point algorithm. If 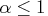 , then
, then 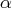 is reduced slightly
by multiplying it by p.
is reduced slightly
by multiplying it by p. 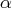 is a value as large as
possible but
is a value as large as
possible but 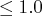 and not so large that an
and not so large that an 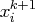 or
or
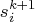 of some variable
of some variable 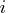 is "too close" to zero.
is "too close" to zero.
- PRSLTYPE=p
- IPRSLTYPE=p
-
Preprocessing the linear programming problem often succeeds
in allowing some variables and constraints to be temporarily eliminated
from the LP that must be solved.
This reduces the solution time
and possibly also the chance that the optimizer will
run into numerical difficulties.
The task of preprocessing is inexpensive to do.
You control how much preprocessing to do by specifying PRSLTYPE=p, where p can be -1, 0, 1, 2, or 3.-1 Do not perform preprocessing. For most problems, specifying PRSLTYPE=-1 is not recommended. 0 Given upper and lower bounds on each variable, the greatest and least contribution to the row activity of each variable is computed. If these are within the limits set by the upper and lower bounds on the row activity, then the row is redundant and can be discarded. Try to tighten the bounds on any of the variables it can. For example, if all coefficients in a constraint are positive and all variables have zero lower bounds, then the row's smallest contribution is zero. If the rhs value of this constraint is zero, then if the constraint type is  or
or 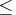 , all the variables in
that constraint can be fixed
to zero. These variables and the constraint can be removed.
If the constraint type is
, all the variables in
that constraint can be fixed
to zero. These variables and the constraint can be removed.
If the constraint type is 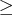 , the constraint is redundant.
If the rhs is negative and the constraint is
, the constraint is redundant.
If the rhs is negative and the constraint is 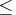 , the
problem is infeasible.
If just one variable in a row is not fixed, use
the row to impose an implicit upper or lower bound on the
variable and then eliminate the row.
The preprocessor also tries to tighten the bounds on
constraint right-hand sides.
, the
problem is infeasible.
If just one variable in a row is not fixed, use
the row to impose an implicit upper or lower bound on the
variable and then eliminate the row.
The preprocessor also tries to tighten the bounds on
constraint right-hand sides.1 When there are exactly two unfixed variables with coefficients in an equality constraint, solve for one in terms of the other. The problem will have one less variable. The new matrix will have at least two fewer coefficients and one less constraint. In other constraints where both variables appear, two coefs are combined into one. PRSLTYPE=0 reductions are also done. 2 It may be possible to determine that an equality constraint is not constraining a variable. That is, if all variables are nonnegative, then 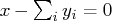 does
not constrain
does
not constrain  , since it must be nonnegative if all the
, since it must be nonnegative if all the
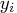 's are nonnegative. In this case, eliminate
's are nonnegative. In this case, eliminate  by
subtracting this equation from all others containing
by
subtracting this equation from all others containing  .
This is useful when the only other entry for
.
This is useful when the only other entry for  is in the
objective function. Perform this reduction if there is
at most one other nonobjective coefficient. PRSLTYPE=0
reductions are also done.
is in the
objective function. Perform this reduction if there is
at most one other nonobjective coefficient. PRSLTYPE=0
reductions are also done.3 All possible reductions are performed. PRSLTYPE=3 is the default.
Preprocessing is iterative. As variables are fixed and eliminated, and constraints are found to be redundant and they too are eliminated, and as variable bounds and constraint right-hand sides are tightened, the LP to be optimized is modified to reflect these changes. Another iteration of preprocessing of the modified LP may reveal more variables and constraints that can be eliminated. - PRINTLEVEL2=p
-
is used when you want to see PROC NETFLOW's progress to the optimum.
PROC NETFLOW will produce a table on the SAS log. A row of
the table is generated during each iteration and may consist of values
of
- the affine step complementarity
- the complementarity of the solution for the next iteration
- the total bound infeasibility
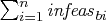 (see the
(see the
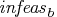 array in the section "Interior Point: Upper Bounds")
array in the section "Interior Point: Upper Bounds")
- the total constraint infeasibility
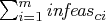 (see the
(see the
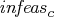 array in the section "Interior Point Algorithmic Details")
array in the section "Interior Point Algorithmic Details")
- the total dual infeasibility
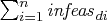 (see the
(see the
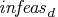 array in the section "Interior Point Algorithmic Details")
array in the section "Interior Point Algorithmic Details")
Interior Point Algorithm Options: Stopping Criteria
- MAXITERB=m
- IMAXITERB=m
-
specifies the maximum number of iterations of the interior point algorithm that can be performed.
The default value for m is 100.
One of the most remarkable aspects of the interior point algorithm is that
for most problems, it usually needs to do a small number of iterations,
no matter the size of the problem.
- PDGAPTOL=p
- RPDGAPTOL=p
-
specifies the primal-dual gap or
duality gap tolerance.
Duality gap is defined in the section "Interior Point Algorithmic Details".
If the relative gap
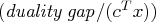 between the primal and dual objectives is smaller than the value
of the PDGAPTOL= option and both the primal and dual problems are feasible,
then PROC NETFLOW stops optimization with a solution that is deemed optimal.
Valid values for p are between 1.0E-12 and 1.0E-1.
The default is 1.0E-7.
between the primal and dual objectives is smaller than the value
of the PDGAPTOL= option and both the primal and dual problems are feasible,
then PROC NETFLOW stops optimization with a solution that is deemed optimal.
Valid values for p are between 1.0E-12 and 1.0E-1.
The default is 1.0E-7.
- STOP_C=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if complementarity
(the value of the Complem-ity
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is
 s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- STOP_DG=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if the duality gap
(the value of the Duality_gap
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is
 s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- STOP_IB=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if total bound infeasibility
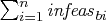 (see the
(see the 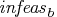 array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=1 or
PRINTLEVEL2=2) is
array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=1 or
PRINTLEVEL2=2) is  s,
optimization will stop.
This option is discussed in the section "Stopping Criteria".
s,
optimization will stop.
This option is discussed in the section "Stopping Criteria".
- STOP_IC=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if total constraint infeasibility
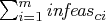 (see the
(see the 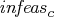 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is  s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- STOP_ID=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if total dual infeasibility
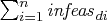 (see the
(see the 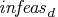 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is  s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- AND_STOP_C=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if complementarity
(the value of the Complem-ity
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is
 s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- AND_STOP_DG=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if the duality gap
(the value of the Duality_gap
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is
 s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- AND_STOP_IB=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if total bound infeasibility
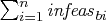 (see the
(see the 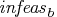 array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is
array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is  s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- AND_STOP_IC=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if total constraint infeasibility
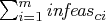 (see the
(see the 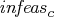 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is  s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- AND_STOP_ID=s
-
is used to determine whether optimization should stop.
At the beginning of each iteration, if total dual infeasibility
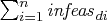 (see the
(see the 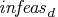 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is  s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
s, and the conditions related to other
AND_STOP parameters are also satisfied, optimization will stop.
This option is discussed in the section "Stopping Criteria".
- KEEPGOING_C=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if complementarity
(the value of the Complem-ity
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- KEEPGOING_DG=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if the duality gap
(the value of the Duality_gap
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- KEEPGOING_IB=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if total bound infeasibility
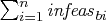 (see the
(see the 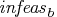 array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- KEEPGOING_IC=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if total constraint infeasibility
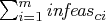 (see the
(see the 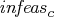 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- KEEPGOING_ID=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if total dual infeasibility
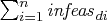 (see the
(see the 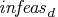 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- AND_KEEPGOING_C=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if complementarity
(the value of the Complem-ity
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- AND_KEEPGOING_DG=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if the duality gap
(the value of the Duality_gap
column in the table produced when you specify
PRINTLEVEL2=1 or PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- AND_KEEPGOING_IB=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if total bound infeasibility
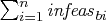 (see the
(see the 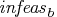 array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
array in the section "Interior Point: Upper Bounds"; this value appears in the Tot_infeasb
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- AND_KEEPGOING_IC=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if total constraint infeasibility
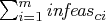 (see the
(see the 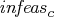 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasc
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
- AND_KEEPGOING_ID=s
-
is used to determine whether optimization should stop.
If a stopping condition is met, if total dual infeasibility
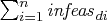 (see the
(see the 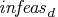 array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
array in the section "Interior Point Algorithmic Details"; this value appears in the Tot_infeasd
column in the table produced when you specify
PRINTLEVEL2=2)
is > s, and the conditions related to other
AND_KEEPGOING parameters are also satisfied, optimization will
continue.
This option is discussed in the section "Stopping Criteria".
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.