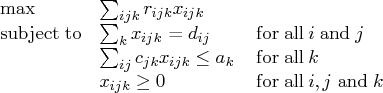| The LP Procedure |
Example 3.12: An Assignment Problem
This example departs somewhat from the emphasis of previous ones. Typically, linear programming models are large, have considerable structure, and are solved with some regularity. Some form of automatic model building, or matrix generation as it is commonly called, is a useful aid. The sparse input format provides a great deal of flexibility in model specification so that, in many cases, the DATA step can be used to generate the matrix.
The following assignment problem illustrates some techniques in matrix generation. In this example, you have four machines that can produce any of six grades of cloth, and you have five customers that demand various amounts of each grade of cloth. The return from supplying a customer with a demanded grade depends on the machine on which the cloth was made. In addition, the machine capacity depends both upon the specific machine used and the grade of cloth made.
To formulate this problem, let 
denote customer,
denote grade, and 
denote machine.
Then let 
denote the amount of cloth of grade made on
machine for customer ;
let 
denote the return from selling
one unit of grade cloth made on machine
to customer ;
let 
denote the demand for
grade cloth by customer ;
let 
denote the number of units of machine
required to produce one
unit of grade cloth;
and let 
denote the
number of units of machine available.
Then, you get
The data are saved in three data sets. The OBJECT data set contains the returns for satisfying demand, the DEMAND data set contains the amounts demanded, and the RESOURCE data set contains the conversion factors for each grade and the total amounts of machine resources available.
title 'An Assignment Problem';
data object;
input machine customer
grade1 grade2 grade3 grade4 grade5 grade6;
datalines;
1 1 102 140 105 105 125 148
1 2 115 133 118 118 143 166
1 3 70 108 83 83 88 86
1 4 79 117 87 87 107 105
1 5 77 115 90 90 105 148
2 1 123 150 125 124 154 .
2 2 130 157 132 131 166 .
2 3 103 130 115 114 129 .
2 4 101 128 108 107 137 .
2 5 118 145 130 129 154 .
3 1 83 . . 97 122 147
3 2 119 . . 133 163 180
3 3 67 . . 91 101 101
3 4 85 . . 104 129 129
3 5 90 . . 114 134 179
4 1 108 121 79 . 112 132
4 2 121 132 92 . 130 150
4 3 78 91 59 . 77 72
4 4 100 113 76 . 109 104
4 5 96 109 77 . 105 145
;
data demand;
input customer
grade1 grade2 grade3 grade4 grade5 grade6;
datalines;
1 100 100 150 150 175 250
2 300 125 300 275 310 325
3 400 0 400 500 340 0
4 250 0 750 750 0 0
5 0 600 300 0 210 360
;
data resource;
input machine
grade1 grade2 grade3 grade4 grade5 grade6 avail;
datalines;
1 .250 .275 .300 .350 .310 .295 744
2 .300 .300 .305 .315 .320 . 244
3 .350 . . .320 .315 .300 790
4 .280 .275 .260 . .250 .295 672
;
The linear program is built using the DATA step. The model is saved in a SAS data set in the sparse input format for PROC LP. Each section of the following DATA step generates a piece of the linear program. The first section generates the objective function; the next section generates the demand constraints; and the last section generates the machine resource availability constraints.
/* build the linear programming model */
data model;
array grade{6} grade1-grade6;
length _type_ $ 8 _row_ $ 8 _col_ $ 8;
keep _type_ _row_ _col_ _coef_;
ncust=5;
nmach=4;
ngrade=6;
/* generate the objective function */
_type_='MAX';
_row_='OBJ';
do k=1 to nmach;
do i=1 to ncust;
link readobj; /* read the objective coefficient data */
do j=1 to ngrade;
if grade{j}^=. then do;
_col_='X'||put(i,1.)||put(j,1.)||put(k,1.);
_coef_=grade{j};
output;
end;
end;
end;
end;
/* generate the demand constraints */
do i=1 to ncust;
link readdmd; /* read the demand data */
do j=1 to ngrade;
if grade{j}^=. then do;
_type_='EQ';
_row_='DEMAND'||put(i,1.)||put(j,1.);
_col_='_RHS_';
_coef_=grade{j};
output;
_type_=' ';
do k=1 to nmach;
_col_='X'||put(i,1.)||put(j,1.)||put(k,1.);
_coef_=1.0;
output;
end;
end;
end;
end;
/* generate the machine constraints */
do k=1 to nmach;
link readres; /* read the machine data */
_type_='LE';
_row_='MACHINE'||put(k,1.);
_col_='_RHS_';
_coef_=avail;
output;
_type_=' ';
do i=1 to ncust;
do j=1 to ngrade;
if grade{j}^=. then do;
_col_='X'||put(i,1.)||put(j,1.)||put(k,1.);
_coef_=grade{j};
output;
end;
end;
end;
end;
readobj: set object;
return;
readdmd: set demand;
return;
readres: set resource;
return;
run;
With the model built and saved in a data set, it is ready for solution using PROC LP. The following program solves the model and saves the solution in the data set called PRIMAL:
/* solve the linear program */
proc lp data=model sparsedata noprint primalout=primal;
run;
The following output is produced by PROC LP.
Output 3.12.1: An Assignment Problem
The solution is prepared for reporting using the DATA step, and a report is written using PROC TABULATE.
/* report the solution */
data solution;
set primal;
keep customer grade machine amount;
if substr(_var_,1,1)='X' then do;
if _value_^=0 then do;
customer = substr(_var_,2,1);
grade = substr(_var_,3,1);
machine = substr(_var_,4,1);
amount = _value_;
output;
end;
end;
run;
proc tabulate data=solution;
class customer grade machine;
var amount;
table (machine*customer), (grade*amount);
run;
The report shown in Output 3.12.2 gives the assignment of customer, grade of cloth, and machine that maximizes the return and does not violate the machine resource availability.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.