Previous Page

|

Next Page

IPNLP Solver Options

This section describes the options recognized by the IPNLP solver. These options can be specified after a forward slash (/) in the SOLVE statement, provided that the IPNLP solver is explicitly specified using a WITH clause.

Details of the currently available options are described as follows:

MAXITER=

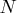
specifies that the solver take at most 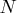major iterations to determine an optimum of the NLP problem. The value of 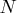is an integer between zero and the largest four-byte, signed integer, which is 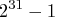. A major iteration in IPNLP consists of finding a descent direction and a step size along which the next approximation of the optimum will reside. The default value of 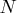is 5000 iterations.

MAXTIME=

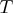
specifies an upper limit of 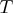seconds of real time for the solver to find a local optimum. Note that the time specified by the MAXTIME= option is checked only once at the end of each major iteration. The default value is 7200 seconds (2 hours).

OPTTOL=

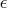
defines the measure by which the user can decide whether the current iterate is an acceptable approximation of a local minimum. The value of this option is a positive real number. The IPNLP solver determines that the current iterate is a local minimum when the norm of the scaled vector of the optimality conditions is less than 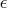. The default value is 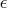=1E - 6.

PRINTFREQ=

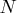
specifies how often the iterations are to be displayed in the SAS log. 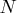should be an integer between zero and the largest four-byte, signed integer, which is 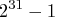. If 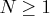, the solver prints only those iterations that are a multiple o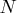f . If 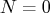, no iteration is displayed in the log. The default value is PRINTFREQ=1.