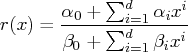Introduction to Optimization

PROC OPTMODEL

Modeling a Linear Programming Problem

Consider the candy manufacturer's problem described in the section "PROC OPTLP". You can formulate the problem using PROC OPTMODEL and solve it using the primal simplex solver as follows:

  
 proc optmodel; 
  
   /* declare variables */ 
   var choco, toffee; 
  
   /* maximize objective function (profit) */ 
   maximize profit = 0.25*choco + 0.75*toffee; 
  
   /* subject to constraints */ 
   con process1: 15*choco + 40*toffee    <= 27000; 
   con process2:            56.25*toffee <= 27000; 
   con process3: 18.75*choco             <= 27000; 
   con process4: 12*choco + 50*toffee    <= 27000; 
  
   /* solve LP using primal simplex solver */ 
   solve with lp / solver = primal_spx; 
  
   /* display solution */ 
   print choco toffee; 
 quit;
 

The optimal objective value and the optimal solution are displayed in the following summary output:

  
                  The OPTMODEL Procedure 
  
                     Solution Summary 
  
          Solver                  Primal Simplex 
          Objective Function              profit 
          Solution Status                Optimal 
          Objective Value                    475 
          Iterations                           3 
  
          Primal Infeasibility                 0 
          Dual Infeasibility                   0 
          Bound Infeasibility                  0 
  
  
                     choco    toffee 
  
                      1000       300
 

You can observe from the preceding example that PROC OPTMODEL provides an easy and intuitive way of modeling and solving mathematical programming models.

Modeling a Nonlinear Programming Problem

The following optimization problem illustrates how you can use some features of PROC OPTMODEL to formulate and solve nonlinear programming problems. The objective of the problem is to find coefficients for an approximation function that matches the values of a given function, , at a set of points . The approximation is a rational function with degree in the numerator and denominator:

The problem can be formulated by minimizing the sum of squared errors at each point in :

The following code implements this model. The function is approximated over a set of points in the range 0 to 1. The function values are saved in a data set that is used by PROC OPTMODEL to set model parameters:

  
    data points; 
       /* generate data points */ 
       keep f x; 
       do i = 0 to 100; 
          x = i/100; 
          f = 2**x; 
          output; 
       end; 
  
    proc optmodel; 
       /* declare, read, and save our data points */ 
       set points; 
       number f{points}; 
       read data points into points = [x] f; 
  
       /* declare variables and model parameters */ 
       number d=1; /* linear polynomial */ 
       var a{0..d}; 
       var b{0..d} init 1; 
       constraint fixb0: b[0] = 1; 
  
       /* minimize sum of squared errors */ 
       min z=sum{x in points} 
                   ((a[0] + sum{i in 1..d} a[i]*x**i) / 
                    (b[0] + sum{i in 1..d} b[i]*x**i) - f[x])**2; 
  
       /* solve and show coefficients */ 
       solve; 
       print a b; 
       quit;
 

The expression for the objective z is defined using operators that parallel the mathematical form. In this case the polynomials in the rational function are linear, so is equal to 1.

The constraint fixb0 forces the constant term of the rational function denominator, b[0], to equal 1. This causes the resulting coefficients to be normalized. The OPTMODEL presolver preprocesses the problem to remove the constraint. An unconstrained solver is used after substituting for b[0].

The SOLVE statement selects a solver, calls it, and displays the status. The PRINT command then prints the values of coefficient arrays a and b:

  
               The OPTMODEL Procedure 
  
                  Solution Summary 
  
          Solver                      L-BFGS 
          Objective Function               z 
          Solution Status            Optimal 
          Objective Value       0.0000590999 
          Iterations                      21 
  
          Optimality Error      3.9537991E-7 
  
  
            [1]           a           b 
  
             0      0.99817     1.00000 
             1      0.42064    -0.29129
 

The approximation for between 0 and 1 is therefore