Input and Output Data Sets :: SAS/OR(R) 14.1 User's Guide: Mathematical Programming Legacy Procedures

DATA= Input Data Set

The DATA= data set is used only to specify an objective function f that is a combination of m other functions $f_ i$ . For each function $f_ i$ , $i=1,\ldots ,m$ , listed in a MAX , MIN , or LSQ statement, each observation l, $l=1,\ldots ,\mi{nobs}$ , in the DATA= data set defines a specific function $f_{il}$ that is evaluated by substituting the values of the variables of this observation into the program statements. If the MAX or MIN statement is used, the $m \times \mi{nobs}$ specific functions $f_{il}$ are added to a single objective function f. If the LSQ statement is used, the sum-of-squares f of the $m \times \mi{nobs}$ specific functions $f_{il}$ is minimized. The NOMISS option causes observations with missing values to be skipped.

INEST= Input Data Set

The INEST= (or INVAR=, or ESTDATA=) input data set can be used to specify the initial values of the parameters defined in a DECVAR statement as well as boundary constraints and the more general linear constraints which could be imposed on these parameters. This form of input is similar to the dense format input used in PROC LP.

The variables of the INEST= data set are

a character variable _TYPE_ that indicates the type of the observation
n numeric variables with the parameter names used in the DECVAR statement
the BY variables that are used in a DATA= input data set
a numeric variable _RHS_ specifying the right-hand-side constants (needed only if linear constraints are used)
additional variables with names corresponding to constants used in the program statements

The content of the _TYPE_ variable defines the meaning of the observation of the INEST= data set. PROC NLP recognizes the following _TYPE_ values:

PARMS, which specifies initial values for parameters. Additional variables can contain the values of constants that are referred to in program statements. The values of the constants in the PARMS observation initialize the constants in the program statements.
UPPERBD | UB, which specifies upper bounds. A missing value indicates that no upper bound is specified for the parameter.
LOWERBD | LB, which specifies lower bounds. A missing value indicates that no lower bound is specified for the parameter.
LE | $<=$ | <, which specifies linear constraint $\sum _ j a_{ij} x_ j \leq b_ i$ . The n parameter values contain the coefficients $a_{ij}$ , and the _RHS_ variable contains the right-hand side $b_ i$ . Missing values indicate zeros.
GE | $>=$ | >, which specifies linear constraint $\sum _ j a_{ij} x_ j \geq b_ i$ . The n parameter values contain the coefficients $a_{ij}$ , and the _RHS_ variable contains the right-hand side $b_ i$ . Missing values indicate zeros.
EQ | =, which specifies linear constraint $\sum _ j a_{ij} x_ j = b_ i$ . The n parameter values contain the coefficients $a_{ij}$ , and the _RHS_ variable contains the right-hand side $b_ i$ . Missing values indicate zeros.

The constraints specified in an INEST= data set are added to the constraints specified in the BOUNDS and LINCON statements. You can use an OUTEST= data set as an INEST= data set in a subsequent run of PROC NLP. However, be aware that the OUTEST= data set also contains the boundary and general linear constraints specified in the previous run of PROC NLP. When you are using this OUTEST= data set without changes as an INEST= data set, PROC NLP adds the constraints from the data set to the constraints specified by a BOUNDS and LINCON statement. Although PROC NLP automatically eliminates multiple identical constraints you should avoid specifying the same constraint twice.

INQUAD= Input Data Set

Two types of INQUAD= data sets can be used to specify the objective function of a quadratic programming problem for TECH= QUADAS or TECH= LICOMP,

$f(x) = \frac{1}{2} x^ T G x + g^ T x + c, \quad \mbox{with} \quad G^ T = G$

The dense INQUAD= data set must contain all numerical values of the symmetric matrix G, the vector g, and the scalar c. Using the sparse INQUAD= data set enables you to specify only the nonzero positions in matrix G and vector g. Those locations that are not set by the sparse INQUAD= data set are assumed to be zero.

Dense INQUAD= Data Set

A dense INQUAD= data set must contain two character variables, _TYPE_ and _NAME_, and at least n numeric variables whose names are the parameter names. The _TYPE_ variable takes the following values:

QUAD lists the n values of the row of the G matrix that is defined by the parameter name used in the _NAME_ variable.
LINEAR lists the n values of the g vector.
CONST sets the value of the scalar c and cannot contain different numerical values; however, it could contain up to $n-1$ missing values.
PARMS specifies initial values for parameters.
UPPERBD | UB specifies upper bounds. A missing value indicates that no upper bound is specified.
LOWERBD | LB specifies lower bounds. A missing value indicates that no lower bound is specified.
LE | $<=$ | < specifies linear constraint $\sum _ j a_{ij} x_ j \leq b_ i$ . The n parameter values contain the coefficients $a_{ij}$ , and the _RHS_ variable contains the right-hand side $b_ i$ . Missing values indicate zeros.
GE | $>=$ | > specifies linear constraint $\sum _ j a_{ij} x_ j \geq b_ i$ . The n parameter values contain the coefficients $a_{ij}$ , and the _RHS_ variable contains the right-hand side $b_ i$ . Missing values indicate zeros.
EQ | = specifies linear constraint $\sum _ j a_{ij} x_ j = b_ i$ . The n parameter values contain the coefficients $a_{ij}$ , and the _RHS_ variable contains the right-hand side $b_ i$ . Missing values indicate zeros.

Constraints specified in a dense INQUAD= data set are added to the constraints specified in BOUNDS and LINCON statements.

Sparse INQUAD= Data Set

A sparse INQUAD= data set must contain three character variables _TYPE_, _ROW_, and _COL_, and one numeric variable _VALUE_. The _TYPE_ variable can assume two values:

QUAD specifies that the _ROW_ and _COL_ variables define the row and column locations of the values in the G matrix.
LINEAR specifies that the _ROW_ variable defines the row locations of the values in the g vector. The _COL_ variable is not used.

Using both the MODEL= option and the INCLUDE statement with the same model file will include the file twice (erroneous in most cases).

OUT= Output Data Set

The OUT= data set contains those variables of a DATA= input data set that are referred to in the program statements and additional variables computed by the program statements for the objective function. Specifying the NOMISS option enables you to skip observations with missing values in variables used in the program statements. The OUT= data set can also contain first- and second-order derivatives of these variables if the OUTDER= option is specified. The variables and derivatives are the final parameter estimates $x^*$ or (for TECH= NONE) the initial value $x^0$ .

The variables of the OUT= data set are

the BY variables and all other variables that are used in a DATA= input data set and referred to in the program code
a variable _OBS_ containing the number of observations read from a DATA= input data set, where the counting is restarted with the start of each BY group. If there is no DATA= input data set, then _OBS_=1.
a character variable _TYPE_ naming the type of the observation
the parameter variables listed in the DECVAR statement
the function variables listed in the MIN , MAX , or LSQ statement
all other variables computed in the program statements
the character variable _WRT_ (if OUTDER= 1) containing the with respect to variable for which the first-order derivatives are written in the function variables
the two character variables _WRT1_ and _WRT2_ (if OUTDER= 2) containing the two with respect to variables for which the first- and second-order derivatives are written in the function variables

OUTEST= Output Data Set

The OUTEST= or OUTVAR= output data set saves the optimization solution of PROC NLP. You can use the OUTEST= or OUTVAR= data set as follows:

to save the values of the objective function on grid points to examine, for example, surface plots using PROC G3D (use the OUTGRID option)
to avoid any costly computation of analytical (first- or second-order) derivatives during optimization when they are needed only upon termination. In this case a two-step approach is recommended:
1. In a first execution, the optimization is done; that is, optimal parameter estimates are computed, and the results are saved in an OUTEST= data set.
2. In a subsequent execution, the optimal parameter estimates in the previous OUTEST= data set are read in an INEST= data set and used with TECH= NONE to compute further results, such as analytical second-order derivatives or some kind of covariance matrix.
to restart the procedure using parameter estimates as initial values
to split a time-consuming optimization problem into a series of smaller problems using intermediate results as initial values in subsequent runs. (Refer to the MAXTIME= , MAXIT= , and MAXFUNC= options to trigger stopping.)
to write the value of the objective function, the parameter estimates, the time in seconds starting at the beginning of the optimization process and (if available) the gradient to the OUTEST= data set during the iterations. After the PROC NLP run is completed, the convergence progress can be inspected by graphically displaying the iterative information. (Refer to the OUTITER option.)

The variables of the OUTEST= data set are

the BY variables that are used in a DATA= input data set
a character variable _TECH_ naming the optimization technique used
a character variable _TYPE_ specifying the type of the observation
a character variable _NAME_ naming the observation. For a linear constraint, the _NAME_ variable indicates whether the constraint is active at the solution. For the initial observations, the _NAME_ variable indicates if the number in the _RHS_ variable corresponds to the number of positive, negative, or zero eigenvalues.
n numeric variables with the parameter names used in the DECVAR statement. These variables contain a point x of the parameter space, lower or upper bound constraints, or the coefficients of linear constraints.
a numeric variable _RHS_ (right-hand side) that is used for the right-hand-side value $b_ i$ of a linear constraint or for the value $f=f(x)$ of the objective function at a point x of the parameter space
a numeric variable _ITER_ that is zero for initial values, equal to the iteration number for the OUTITER output, and missing for the result output

The _TYPE_ variable identifies how to interpret the observation. If _TYPE_ is

PARMS then parameter-named variables contain the coordinates of the resulting point $x^{*}$ . The _RHS_ variable contains $f(x^*)$ .
INITIAL then parameter-named variables contain the feasible starting point $x^{(0)}$ . The _RHS_ variable contains $f(x^{(0)})$ .
GRIDPNT then (if the OUTGRID option is specified) parameter-named variables contain the coordinates of any point $x^{(k)}$ used in the grid search. The _RHS_ variable contains $f(x^{(k)})$ .
GRAD then parameter-named variables contain the gradient at the initial or final estimates.
STDERR then parameter-named variables contain the approximate standard errors (square roots of the diagonal elements of the covariance matrix) if the COV= option is specified.
_NOBS_ then (if the COV= option is specified) all parameter variables contain the value of _NOBS_ used in computing the $\sigma ^2$ value in the formula of the covariance matrix.
UPPERBD | UB then (if there are boundary constraints) the parameter variables contain the upper bounds.
LOWERBD | LB then (if there are boundary constraints) the parameter variables contain the lower bounds.
NACTBC then all parameter variables contain the number $n_{abc}$ of active boundary constraints at the solution $x^*$ .
ACTBC then (if there are active boundary constraints) the observation indicate which parameters are actively constrained, as follows:

_NAME_=GE

the active lower bounds

_NAME_=LE

the active upper bounds

_NAME_=EQ

the active equality constraints
NACTLC then all parameter variables contain the number $n_{alc}$ of active linear constraints that are recognized as linearly independent.
NLDACTLC then all parameter variables contain the number of active linear constraints that are recognized as linearly dependent.
LE then (if there are linear constraints) the observation contains the ith linear constraint $\sum _ j a_{ij} x_ j \leq b_ i$ . The parameter variables contain the coefficients 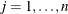$a_{ij}$ , $j=1,\ldots ,n$ , and the _RHS_ variable contains $b_ i$ . If the constraint i is active at the solution $x^{*}$ , then _NAME_=ACTLC or _NAME_=LDACTLC.
GE then (if there are linear constraints) the observation contains the ith linear constraint $\sum _ j a_{ij} x_ j \geq b_ i$ . The parameter variables contain the coefficients 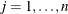$a_{ij}$ , $j=1,\ldots ,n$ , and the _RHS_ variable contains $b_ i$ . If the constraint i is active at the solution $x^{*}$ , then _NAME_=ACTLC or _NAME_=LDACTLC.
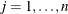EQ then (if there are linear constraints) the observation contains the ith linear constraint $\sum _ j a_{ij} x_ j = b_ i$ . The parameter variables contain the coefficients $a_{ij}$ , $j=1,\ldots ,n$ , the _RHS_ variable contains $b_ i$ , and _NAME_=ACTLC or _NAME_=LDACTLC.
LAGRANGE then (if at least one of the linear constraints is an equality constraint or an active inequality constraint) the observation contains the vector of Lagrange multipliers. The Lagrange multipliers of active boundary constraints are listed first followed by those of active linear constraints and those of active nonlinear constraints. Lagrange multipliers are available only for the set of linearly independent active constraints.
PROJGRAD then (if there are linear constraints) the observation contains the $n - n_\mi {act}$ values of the projected gradient $g_ Z = Z^ T g$ in the variables corresponding to the first $n-n_\mi {act}$ parameters.
JACOBIAN then (if the PJACOBI or OUTJAC option is specified) the m observations contain the m rows of the $m \times n$ Jacobian matrix. The _RHS_ variable contains the row number l, $l=1,\ldots ,m$ .
HESSIAN then the first n observations contain the n rows of the (symmetric) Hessian matrix. The _RHS_ variable contains the row number j, 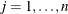$j=1,\ldots ,n$ , and the _NAME_ variable contains the corresponding parameter name.
PROJHESS then the first $n - n_\mi {act}$ observations contain the $n-n_\mi {act}$ rows of the projected Hessian matrix $Z^ TGZ$ . The _RHS_ variable contains the row number j, $j=1,\ldots ,n-n_\mi {act}$ , and the _NAME_ variable is blank.
CRPJAC then the first n observations contain the n rows of the (symmetric) crossproduct Jacobian matrix at the solution. The _RHS_ variable contains the row number j, 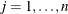$j=1,\ldots ,n$ , and the _NAME_ variable contains the corresponding parameter name.
PROJCRPJ then the first $n - n_\mi {act}$ observations contain the $n-n_\mi {act}$ rows of the projected crossproduct Jacobian matrix $Z^ T(J^ TJ)Z$ . The _RHS_ variable contains the row number j, $j=1,\ldots ,n-n_{act}$ , and the _NAME_ variable is blank.
COV1, COV2, COV3, COV4, COV5, or COV6 then (depending on the COV= option) the first n observations contain the n rows of the (symmetric) covariance matrix of the parameter estimates. The _RHS_ variable contains the row number j, 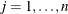$j=1,\ldots ,n$ , and the _NAME_ variable contains the corresponding parameter name.
DETERMIN contains the determinant $\mi{det} = a \times 10^ b$ of the matrix specified by the value of the _NAME_ variable where a is the value of the first variable in the DECVAR statement and b is in _RHS_.
NEIGPOS, NEIGNEG, or NEIGZER then the _RHS_ variable contains the number of positive, negative, or zero eigenvalues of the matrix specified by the value of the _NAME_ variable.
COVRANK then the _RHS_ variable contains the rank of the covariance matrix.
SIGSQ then the _RHS_ variable contains the scalar factor of the covariance matrix.
_TIME_ then (if the OUTITER option is specified) the _RHS_ variable contains the number of seconds passed since the start of the optimization.
TERMINAT then if optimization terminated at a point satisfying one of the termination criteria, an abbreviation of the corresponding criteria is given to the _NAME_ variable. Otherwise _NAME_=PROBLEMS.

If for some reason the procedure does not terminate successfully (for example, no feasible initial values can be computed or the function value or derivatives at the starting point cannot be computed), the OUTEST= data set may contain only part of the observations (usually only the PARMS and GRAD observation).

Note: Generally you can use an OUTEST= data set as an INEST= data set in a further run of PROC NLP. However, be aware that the OUTEST= data set also contains the boundary and general linear constraints specified in the previous run of PROC NLP. When you are using this OUTEST= data set without changes as an INEST= data set, PROC NLP adds the constraints from the data set to the constraints specified by a BOUNDS or LINCON statement. Although PROC NLP automatically eliminates multiple identical constraints you should avoid specifying the same constraint twice.

Output of Profiles

The following observations are written to the OUTEST= data set only when the PROFILE statement or CLPARM option is specified.

Table 6.4: Output of Profiles

_TYPE_	_NAME_	_RHS_	Meaning of Observation
PLC_LOW	parname	y value	coordinates of lower CL for $\alpha$
PLC_UPP	parname	y value	coordinates of upper CL for $\alpha$
WALD_CL	LOWER	y value	lower Wald CL for $\alpha$ in _ALPHA_
WALD_CL	UPPER	y value	upper Wald CL for $\alpha$ in _ALPHA_
PL_CL	LOWER	y value	lower PL CL for $\alpha$ in _ALPHA_
PL_CL	UPPER	y value	upper PL CL for $\alpha$ in _ALPHA_
PROFILE	L(THETA)	missing	y value corresponding to x
			in following _NAME_=THETA
PROFILE	THETA	missing	x value corresponding to y
			in previous _NAME_=L(THETA)

Assume that the PROFILE statement specifies $n_ p$ parameters and $n_{\alpha }$ confidence levels. For CLPARM , $n_ p=n$ and $n_{\alpha }=4$ .

_TYPE_=PLC_LOW and _TYPE_=PLC_UPP: If the CLPARM= option or the PROFILE statement with the OUTTABLE option is specified, then the complete set $\theta$ of parameter estimates (rather than only the confidence limit $x=\theta _ j$ ) is written to the OUTEST= data set for each side of the confidence interval. This output may be helpful for further analyses on how small changes in $x=\theta _ j$ affect the changes in the other $\theta _ i, i \neq j$ . The _ALPHA_ variable contains the corresponding value of $\alpha$ . There should be no more than $2n_{\alpha }n_ p$ observations. If the confidence limit cannot be computed, the corresponding observation is not available.
_TYPE_=WALD_CL: If CLPARM= WALD, CLPARM= BOTH, or the PROFILE statement with $\alpha$ values is specified, then the Wald confidence limits are written to the OUTEST= data set for each of the default or specified values of $\alpha$ . The _ALPHA_ variable contains the corresponding value of $\alpha$ . There should be $2n_{\alpha }$ observations.
_TYPE_=PL_CL: If CLPARM= PL, CLPARM= BOTH, or the PROFILE statement with $\alpha$ values is specified, then the PL confidence limits are written to the OUTEST= data set for each of the default or specified values of $\alpha$ . The _ALPHA_ variable contains the corresponding values of $\alpha$ . There should be $2n_{\alpha }$ observations; some observations may have missing values.
_TYPE_=PROFILE: If CLPARM= PL, CLPARM= BOTH, or the CLPARM= statement with or without $\alpha$ values is specified, then a set of $(x,y)$ point coordinates in two adjacent observations with _NAME_=L(THETA) (y value) and _NAME_=THETA (x value) is written to the OUTEST= data set. The _RHS_ and _ALPHA_ variables are not used (are set to missing). The number of observations depends on the difficulty of the optimization problems.

OUTMODEL= Output Data Set

The program statements for objective functions, nonlinear constraints, and derivatives can be saved into an OUTMODEL= output data set. This data set can be used in an INCLUDE program statement or as a MODEL= input data set in subsequent calls of PROC NLP. The OUTMODEL= option is similar to the option used in PROC MODEL in SAS/ETS software.

Storing Programs in Model Files

Models can be saved to and recalled from SAS catalog files. SAS catalogs are special files which can store many kinds of data structures as separate units in one SAS file. Each separate unit is called an entry, and each entry has an entry type that identifies its structure to the SAS system.

In general, to save a model, use the OUTMODEL= name option in the PROC NLP statement, where name is specified as libref.catalog.entry, libref.entry, or entry. The libref, catalog, and entry names must be valid SAS names no more than 8 characters long. The catalog name is restricted to 7 characters on the CMS operating system. If not given, the catalog name defaults to MODELS, and the libref defaults to WORK. The entry type is always MODEL. Thus, OUTMODEL= X writes the model to the file WORK.MODELS.X.MODEL.

The MODEL= option is used to read in a model. A list of model files can be specified in the MODEL= option, and a range of names with numeric suffixes can be given, as in MODEL=(MODEL1-MODEL10). When more than one model file is given, the list must be placed in parentheses, as in MODEL=(A B C). If more than one model file is specified, the files are combined in the order listed in the MODEL= option.

When the MODEL= option is specified in the PROC NLP statement and model definition statements are also given later in the PROC NLP step, the model files are read in first, in the order listed, and the model program specified in the PROC NLP step is appended after the model program read from the MODEL= files.

The INCLUDE statement can be used to append model code to the current model code. The contents of the model files are inserted into the current model at the position where the INCLUDE statement appears.

Note that the following statements are not part of the program code that is written to an OUTMODEL= data set: MIN , MAX , LSQ , MINQUAD , MAXQUAD , DECVAR , BOUNDS , BY , CRPJAC , GRADIENT , HESSIAN , JACNLC , JACOBIAN , LABEL , LINCON , MATRIX , and NLINCON .

The NLP Procedure