The CLP Procedure

Example 3.12 Scheduling a Major Basketball Conference

Example 1.8 illustrated how you could use the CLP procedure to solve a single round-robin problem by modeling it as a scheduling CSP. This example illustrates an alternate way of modeling and solving a well-known double round-robin problem using the CLP procedure. This example is based on the work of Nemhauser and Trick (1998) and deals with scheduling the Atlantic Coast Conference (ACC) Men’s Basketball games for the 1997–1998 season.

A temporally dense double round-robin (DDRR) for teams is a double round-robin in which the games are played over a minimal number of dates or time slots. If is even, the number of slots is and each team plays in every time slot. If is odd, the number of slots is and teams play in each time slot. In the latter case, each time slot has a team with a bye, and each team has two byes for the season.

The Atlantic Coast Conference (ACC) 1997–1998 men’s basketball scheduling problem as described in Nemhauser and Trick (1998) and Henz (2001) is a DDRR that consists of the following nine teams with their abbreviated team name and team number shown in parentheses: Clemson (Clem 1), Duke (Duke 2), Florida State (FSU 3), Georgia Tech (GT 4), Maryland (UMD 5), University of North Carolina (UNC 6), NC State (NCSU 7), Virginia (UVA 8), and Wake Forest (Wake 9).

The general objective is to schedule the DDRR to span the months of January and February and possibly include a game in December or March or both. In general, each team plays twice a week—typically Wednesday and Saturday. Although the actual day might differ, these two time slots are referred to as the “weekday slot” and the “weekend slot.” Since there are an odd number of teams, there is a team with a bye in each slot and four games in each slot, resulting in a schedule that requires 18 time slots or nine weeks. The last time slot must be a weekend slot, which implies the first slot is a weekday slot. The first slot, denoted slot 1, corresponds to the last weekday slot of December 1997, and the final slot, slot 18, corresponds to the first weekend slot of March 1998. Each team plays eight home games and eight away games, and has two byes.

In addition there are several other constraints that must be satisfied. This example uses the following criteria employed by Nemhauser and Trick (1998) as presented by Henz (2001).

Mirroring: The dates are grouped into pairs 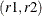, such that each team gets to play against the same team in dates 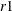and 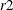. Such a grouping is called a mirroring scheme. A separation of nine slots can be achieved by mirroring a round-robin schedule; while this separation is desirable, it is not possible for this problem.

Nemhauser and Trick fix the mirroring scheme to

$m = (1, 8), (2, 9), (3, 12), (4, 13), (5, 14), (6, 15), (7, 16), (10, 17), (11, 18)$

in order to satisfy the constraints that UNC and Duke play in time slots 11 and 18. (See criterion 9.)

Initial and final home and away games: Every team must play at home on at least one of the first three dates. Every team must play at home on at least one of the last three dates. No team can play away on both of the last two dates.
Home/away/bye pattern: No team can have more than two away games in a row. No team can have more than two home games in a row. No team can have more than three away games or byes in a row. No team can have more than four home games or byes in a row.
Weekend pattern: Of the nine weekends, each team plays four at home, four away, and has one bye.
First weekends: Each team must have home games or byes on at least two of the first five weekends.
Rival matches: Every team except FSU has a traditional rival. The rival pairs are Clem-GT, Duke-UNC, UMD-UVA, and NCSU-Wake. In the last date, every team except FSU plays against its rival, unless it plays against FSU or has a bye.
Popular matches in February: The following pairings must occur at least once in dates 11 to 18: Duke-GT, Duke-Wake, GT-UNC, UNC-Wake.
Opponent sequence: No team plays in two consecutive away dates against Duke and UNC. No team plays in three consecutive dates against Duke, UNC, and Wake (independent of the home or away status).
Idiosyncrasies: UNC plays its rival Duke in the last date and in date 11. UNC plays Clem in the second date. Duke has a bye in date 16. Wake does not play home in date 17. Wake has a bye in the first date. Clem, Duke, UMD and Wake do not play away in the last date. Clem, FSU, and GT do not play away in the first date. Neither FSU nor NCSU has a bye in last date. UNC does not have a bye in the first date.

Previous work for solving round-robin problems, including that of Nemhauser and Trick (1998) and Henz (2001), have used a general three-phase framework for finding good schedules.

pattern generation
pattern set generation
timetable generation

A pattern is a valid sequence of home, away, and bye games for a given team for the entire season. For example, the following is a valid pattern:

A H B A H H A H A A H B H A A H H A

For this example, patterns that satisfy criterion 1 through criterion 5 and some constraints in criterion 9 are generated using the CLP procedure with the SAS macro %PATTERNS.

/****************************************************************/
/* First, find all possible patterns. Consider only time        */
/* constraints at this point. A pattern should be suitable      */
/* for any team. Do not consider individual teams yet.          */
/****************************************************************/
%macro patterns();

proc clp out=all_patterns findall;
   /* For date 1 to 18. */
   %do j = 1 %to 18;
      var h&j = [0, 1]; /* home */
      var a&j = [0, 1]; /* away */
      var b&j = [0, 1]; /* bye */

      /* A team is either home, away, or bye. */
      lincon h&j + a&j + b&j=1;
   %end;

   /*------------------------------------------------------------*/
   /* Criterion 1 - Mirroring Scheme                             */
   /*------------------------------------------------------------*/
   /* The dates are grouped into pairs (j, j1), such that each   */
   /* team plays the same opponent on dates j and j1.            */
   /* A home game on date j will be an away game on date j1      */
   %do j = 1 %to 18;
      %do j1 = %eval(&j+1) %to 18;
         %if ( &j=1 and &j1=8 ) or ( &j=2 and &j1=9 ) or
             ( &j=3 and &j1=12 ) or ( &j=4 and &j1=13 ) or
             ( &j=5 and &j1=14 ) or ( &j=6 and &j1=15 ) or
             ( &j=7 and &j1=16 ) or ( &j=10 and &j1=17 ) or
             ( &j=11 and &j1=18 ) %then
            lincon h&j = a&j1, a&j = h&j1, b&j = b&j1;;
      %end;
   %end;

   /*------------------------------------------------------------*/
   /* Criterion 2 - Initial and Final Home and Away Games        */
   /*------------------------------------------------------------*/
   /* Every team must play home on at least one of the first three dates. */
   lincon h1 + h2 + h3 >= 1;

   /* Every team must play home on at least one of the last three dates. */
   lincon h16 + h17 + h18 >= 1;

   /* No team can play away on both last two dates. */
   lincon a17 + a18 < 2;

   /*------------------------------------------------------------*/
   /* Criterion 3 - Home/Away/Bye Pattern                        */
   /*------------------------------------------------------------*/
   %do j = 1 %to 16;
      /* No team can have more than two away matches in a row.*/
      lincon a&j + a%eval(&j+1) + a%eval(&j+2) < 3;
      /* No team can have more than two home matches in a row.*/
      lincon h&j + h%eval(&j+1) + h%eval(&j+2) < 3;
   %end;

   /* No team can have more than three away matches or byes in a row.*/
   %do j = 1 %to 15;
      lincon a&j + b&j + a%eval(&j+1) + b%eval(&j+1) + a%eval(&j+2)
             + b%eval(&j+2) + a%eval(&j+3) + b%eval(&j+3) < 4;
   %end;

   /* No team can have more than four home matches or byes in a row.*/
   %do j = 1 %to 14;
       lincon h&j + b&j + h%eval(&j+1) + b%eval(&j+1) + h%eval(&j+2)
              + b%eval(&j+2) + h%eval(&j+3) + b%eval(&j+3) + h%eval(&j+4)
              + b%eval(&j+4) < 5;
   %end;

   /*------------------------------------------------------------*/
   /* Criterion 4 - Weekend Pattern                              */
   /*------------------------------------------------------------*/
   /* Each team plays four weekends at home. */
   lincon 0 %do j = 2 %to 18 %by 2; +h&j %end; =4;
   /* Each team plays four weekends away. */
   lincon 0 %do j = 2 %to 18 %by 2; +a&j %end; =4;
   /* Each team has 1 weekend with a bye  */
   lincon 0 %do j = 2 %to 18 %by 2; +b&j %end; =1;

   /*------------------------------------------------------------*/
   /* Criterion 5 - First Weekends                               */
   /*------------------------------------------------------------*/
   /* Each team must have home games or byes on at least two     */
   /* of the first five weekends.                                */
   lincon 0 %do j = 2 %to 10 %by 2; + h&j + b&j %end; >=2;

   /*------------------------------------------------------------*/
   /* Criterion 9 - (Partial)                                    */
   /*------------------------------------------------------------*/      
   /* The team with a bye in date 1 does not play away on the    */
   /*    last date or home in date 17 (Wake)                     */
   /* The team with a bye in date 16 does not play away in       */
   /*    date 18 (Duke)                                          */
   lincon b1 + a18 < 2, b1 + h17 < 2, b16 + a18 < 2;
 
run;

%mend;

%patterns;

The %PATTERNS macro generates 38 patterns. The next step is to find a subset of patterns with cardinality equal to the number of teams that would collectively support a potential assignment to all of the teams. For example, each of the 18 time slots must correspond to four home games, four away games, and one bye. Furthermore, pairs of patterns that do not support a potential meeting date between the two corresponding teams are excluded. The following %PATTERN_SETS macro uses the CLP procedure with the preceding constraints to generate 17 possible pattern sets.

/*****************************************************************/
/* Determine all possible "pattern sets" considering only time   */
/* constraints.                                                  */
/* Individual teams are not considered at this stage.            */
/* xi - binary variable indicates pattern i is in pattern set    */
/*****************************************************************/

%macro pattern_sets();

data _null_;
   set all_patterns;
   %do i=1 %to 38;
      if _n_=&i then do;
         %do j=1 %to 18;
            call symput("h&i._&j", put(h&j,best.));
            call symput("a&i._&j", put(a&j,best.));
            call symput("b&i._&j", put(b&j,best.));
         %end;
      end;
   %end;
run;

proc clp out=pattern_sets findall;
   /* xi=1 if pattern i belongs to pattern set */
   var (x1-x38)= [0, 1];

   /* Exactly nine patterns per patterns set */
   lincon 0 %do i = 1 %to 38; + x&i %end;=9;

   /* time slot constraints */
   %do j = 1 %to 18;
      /* Four home games per time slot */
      lincon 0 %do i = 1 %to 38; + &&h&i._&j*x&i %end; =4;
      /* Four away games per time slot */
      lincon 0 %do i = 1 %to 38; + &&a&i._&j*x&i %end; =4;
      /* One bye per time slot */
      lincon 0 %do i = 1 %to 38; + &&b&i._&j*x&i %end; =1;
   %end;

   /* Exclude pattern pairs that do not support a meeting date */
   %do i = 1 %to 38;
      %do i1 = %eval(&i+1) %to 38;
         %let count=0;
         %do j=1 %to 18;
            %if ( (&&h&i._&j=0 or &&a&i1._&j=0) and
                  (&&a&i._&j=0 or &&h&i1._&j=0)) %then %do;
               %let count=%eval(&count+1);
            %end;
         %end;
         %if (&count=18) %then %do;
            lincon x&i+x&i1<=1;
         %end;
      %end;
   %end;
run;

%mend;

%pattern_sets;

The %PATTERN_SETS macro generates 17 pattern sets. The final step is to add the individual team constraints and match up teams to the pattern set in order to come up with a schedule for each team. The schedule for each team indicates the opponent for each time slot (0 for a bye) and whether it corresponds to a home game, away game, or a bye.

The following SAS macro %TIMETABLE uses the pattern set index as a parameter and invokes the CLP procedure with the individual team constraints to determine the team schedule.

/*********************************************************************/
/* Assign individual teams to pattern set k                          */ 
/* Teams: 1 Clem, 2 Duke, 3 FSU, 4 GT, 5 UMD, 6 UNC, 7 NCSU, 8 UVA,  */
/*        9 Wake                                                     */
/*********************************************************************/
%macro timetable(k);

proc clp out=ACC_ds_&k varselect=minrmaxc findall;

   %do j = 1 %to 18;
      /*  alpha(i,j): Team i's opponent on date j ( 0 = bye ). */
      %do i = 1 %to 9;
         var alpha&i._&j = [0, 9];
      %end;

      /* Timetable constraint 1 */
      /* Opponents in a time slot must be distinct */
      alldiff ( %do i = 1 %to 9; alpha&i._&j %end; );

      /* Timetable constraint 2 */
      %do i = 1 %to 9;
         %do i1 = 1 %to 9;
            /* indicates if teams i and i1 play in time slot j */
            var X&i._&i1._&j = [0, 1]; 
            reify X&i._&i1._&j: (alpha&i._&j = &i1);

            /* team i plays i1 iff team i1 plays i */
            %if (&i1 > &i ) %then %do;
               lincon X&i._&i1._&j = X&i1._&i._&j;
            %end;
         %end;
      %end;
   %end;

   /* Mirroring Scheme at team level.                         */ 
   /* The dates are grouped into pairs (j, j1) such that each */
   /* team plays the same opponent in dates j and j1.         */
   /* One of these should be a home game for each team.       */
   %do i = 1 %to 9;
      %do j = 1 %to 18;
         %do j1 = %eval(&j+1) %to 18;
            %if ( &j=1 and &j1=8 ) or ( &j=2 and &j1=9 ) or
                ( &j=3 and &j1=12 ) or ( &j=4 and &j1=13 ) or 
                ( &j=5 and &j1=14 ) or ( &j=6 and &j1=15 ) or 
                ( &j=7 and &j1=16 ) or ( &j=10 and &j1=17 ) or 
                ( &j=11 and &j1=18 ) %then %do;
               lincon alpha&i._&j=alpha&i._&j1,
               /* H and A are matrices that indicate home */
               /* and away games                          */
               H&i._&j=A&i._&j1,  
               H&i._&j1=A&i._&j;
            %end;
         %end;
      %end;
   %end;

   /* Timetable constraint 3 */
   /* Each team plays every other team twice */
   %do i = 1 %to 9;
      %do i1 = 1 %to 9;
         %if &i1 ne &i %then %do;
            lincon 0 %do j = 1 %to 18; + X&i._&i1._&j %end; = 2;
         %end;
      %end;
   %end;

   /* Timetable constraint 4 */
   /* Teams do not play against themselves */
   %do j = 1 %to 18;
      %do i = 1 %to 9;
         lincon alpha&i._&j<>&i;
         lincon X&i._&i._&j = 0;  /* redundant */
      %end;
   %end;

   /* Timetable constraint 5 */
   /* Setup Bye Matrix */
   /* alpha&i._&j=0 means team &i has a bye on date &j. */
   %do j = 1 %to 18;
      %do i = 1 %to 9;
         var B&i._&j = [0, 1]; /*Bye matrix*/
         reify B&i._&j: ( alpha&i._&j = 0 );
      %end;
   %end;

   /* Timetable constraint 6 */
   /* alpha&i._&j=&i1 implies teams &i and &i1 play on date &j */
   /* It must be a home game for one, away game for the other  */
   %do j = 1 %to 18;
      %do i = 1 %to 9;
         %do i1 = 1 %to 9;
            /* reify control variables.*/
            var U&i._&i1._&j = [0, 1] V&i._&i1._&j = [0, 1];

            /* if &i is home and &i1 is away. */
            reify U&i._&i1._&j: ( H&i._&j + A&i1._&j = 2);
            /* if &i1 is home and &i is away. */
            reify V&i._&i1._&j: ( A&i._&j + H&i1._&j = 2);

            /* Necessary condition if &i plays &i1 on date j  */
            lincon X&i._&i1._&j <= U&i._&i1._&j + V&i._&i1._&j;
         %end;
      %end;
   %end;

   /* Timetable constraint 7 */                
   /* Each team must be home, away or have a bye on a given date */
   %do j = 1 %to 18;
      %do i = 1 %to 9;
         /* Team &i is home (away) at date &j. */
         var H&i._&j = [0, 1] A&i._&j = [0, 1];
         lincon H&i._&j + A&i._&j + B&i._&j = 1;
      %end;
   %end;
          
   %do i = 1 %to 9;
      %do i1 = %eval(&i+1) %to 9;
      
         /* Timetable constraint 8 */                 
         /*-------------------------------------------------------*/
         /* Criterion 6 - Rival Matches                           */
         /*-------------------------------------------------------*/
         /* The final weekend is reserved for 'rival games' */
         /* unless the team plays FSU or has a bye          */
         %if ( &i=1 and &i1=4 ) or ( &i=2 and &i1=6 ) or 
             ( &i=5 and &i1=8 ) or ( &i=7 and &i1=9 ) %then %do;
            lincon X&i._&i1._18 + B&i._18 + X&i._3_18 = 1;
            
            /* redundant */
            lincon X&i1._&i._18 + B&i1._18 + X&i1._3_18 = 1;
         %end;

         /* Timetable constraint 9 */                 
         /*-------------------------------------------------------*/
         /* Criterion 7 - Popular Matches                         */
         /*-------------------------------------------------------*/
         /* The following pairings are specified to occur at      */
         /* least once in February.                               */
         %if ( &i=2 and &i1=4 ) or ( &i=2 and &i1=9 ) or
             ( &i=4 and &i1=6 ) or ( &i=6 and &i1=9 ) %then %do;
            lincon 0 %do j = 11 %to 18; + X&i._&i1._&j  %end; >= 1;

            /* redundant */
            lincon 0 %do j = 11 %to 18; + X&i1._&i._&j %end; >= 1;
         %end;
      %end;
   %end;
    
   /* Timetable constraint 10 */       
   /*-------------------------------------------------------*/
   /* Criterion 8 - Opponent Sequence                       */
   /*-------------------------------------------------------*/
   %do i = 1 %to 9;
      /* No team plays two consecutive away dates against   */
      /* Duke (2) and UNC (6)                               */
      %do j = 1 %to 17;
         var Q&i._26_&j = [0, 1] P&i._26_&j = [0, 1]; 
         reify Q&i._26_&j: ( X&i._2_&j +  X&i._6_&j = 1 );
         reify P&i._26_&j: ( X&i._2_%eval(&j+1) +  X&i._6_%eval(&j+1) =1 );
         lincon Q&i._26_&j + A&i._&j + P&i._26_&j + A&i._%eval(&j+1) < 4;
      %end;

      /* No team plays three consecutive dates against      */
      /* Duke(2), UNC(6) and Wake(9).                       */
      %do j = 1 %to 16;
         var L&i._269_&j = [0, 1] M&i._269_&j = [0, 1]
             N&i._269_&j = [0, 1];
         reify L&i._269_&j: ( X&i._2_&j +  X&i._6_&j +  X&i._9_&j = 1 );
         reify M&i._269_&j: ( X&i._2_%eval(&j+1) + X&i._6_%eval(&j+1) +
                              X&i._9_%eval(&j+1) =1 );
         reify N&i._269_&j: ( X&i._2_%eval(&j+2) + X&i._6_%eval(&j+2) +
                              X&i._9_%eval(&j+2) =1 );
         lincon L&i._269_&j + M&i._269_&j + N&i._269_&j  < 3;
      %end;
   %end;

   
   /* Timetable constraint 11 */       
   /*-------------------------------------------------------*/
   /* Criterion 9 - Idiosyncratic Constraints               */
   /*-------------------------------------------------------*/
   /* UNC plays Duke in date 11 and 18 */
   lincon alpha6_11 = 2 ;
   lincon alpha6_18 = 2 ;
   /* UNC plays Clem in the second date. */
   lincon alpha6_2 = 1 ;
   /* Duke has a bye in date 16. */
   lincon B2_16 = 1 ;
   /* Wake does not play home in date 17. */
   lincon H9_17 = 0 ;
   /* Wake has a bye in the first date. */
   lincon B9_1 = 1 ;
   /* Clem, Duke, UMD and Wake do not play away in the last date. */
   lincon A1_18 = 0 ;
   lincon A2_18 = 0 ;
   lincon A5_18 = 0 ;
   lincon A9_18 = 0 ;
   /* Clem, FSU, and GT do not play away in the first date. */
   lincon A1_1 = 0 ;
   lincon A3_1 = 0 ;
   lincon A4_1 = 0 ;
   /* FSU and NCSU do not have a bye in the last date. */
   lincon B3_18 = 0 ;
   lincon B7_18 = 0 ;
   /* UNC does not have a bye in the first date. */
   lincon B6_1 = 0 ;

   /* Timetable constraint 12 */       
   /*-------------------------------------------------------*/  
   /* Match teams with patterns.                            */
   /*-------------------------------------------------------*/
   %do i = 1 %to 9; /* For each team */
      var p&i=[1,9];
      %do j=1 %to 18; /* For each date */   
         element ( p&i, (&&col&k._h_&j), H&i._&j )
                 ( p&i, (&&col&k._a_&j), A&i._&j )
                 ( p&i, (&&col&k._b_&j), B&i._&j );
      %end;
   %end;
run;

%mend;

/**************************************************************/
/* Try all possible pattern sets to find all valid schedules. */
/**************************************************************/

%macro find_schedules;

proc transpose data=pattern_sets out=trans_good; run;
 
data _temp; 
   set trans_good; 
   set all_patterns; 
run; 
 
proc sql noprint; 
   %do k = 1 %to 17; /* For each pattern */ 
      %do j=1 %to 18; /* For each date */ 
         select h&j into :col&k._h_&j 
            separated by ',' from _temp where col&k=1; 
         select a&j into :col&k._a_&j 
            separated by ',' from _temp where col&k=1; 
         select b&j into :col&k._b_&j 
            separated by ',' from _temp where col&k=1; 
      %end; 
   %end; 
run;

 
data all; run; 
 
%do k = 1 %to 17; /* For each pattern set */ 
   %timetable(k=&k); 

   data all; 
      set all ACC_ds_&k; 
   run; 
%end; 
 
data all; 
   set all; 
   if _n_=1 then delete; 
run; 
 
%mend; 
 
%find_schedules;

The %FIND_SCHEDULES macro invokes the %TIMETABLE macro for each of the 17 pattern sets and generates 179 possible schedules including the one that was eventually used by the ACC, which is displayed in Output 3.12.1.

Output 3.12.1: ACC Basketball Tournament Schedule