ROUND Function

The ROUND function rounds the first argument to a value that is very close to a multiple of the second argument. The result might not be an exact multiple of the second argument.

Computers use binary arithmetic with finite precision. If you work with numbers that do not have an exact binary representation, computers often produce results that differ slightly from the results that are produced with decimal arithmetic.

For example, the decimal values 0.1 and 0.3 do not have exact binary representations. In decimal arithmetic, 3*0.1 is exactly equal to 0.3, but this equality is not true in binary arithmetic. As the following example shows, if you write these two values in SAS, they appear the same. If you compute the difference, however, you can see that the values are different.

data _null_;
   point_three=0.3;   
   three_times_point_one=3*0.1;  
   difference=point_three - three_times_point_one;
   put point_three= ; 
   put three_times_point_one= ;
   put difference= ; 
run; 

The following lines are written to the SAS log:

   point_three= 0.3
   three_times_point_one= 0.3
   difference= -5.55112E-17

Rounding by definition finds an exact multiple of the rounding unit that is closest to the value to be rounded. For example, 0.33 rounded to the nearest tenth equals 3*0.1 or 0.3 in decimal arithmetic. In binary arithmetic, 0.33 rounded to the nearest tenth equals 3*0.1, and not 0.3, because 0.3 is not an exact multiple of one tenth in binary arithmetic.

The ROUND function returns the value that is based on decimal arithmetic, even though this value is sometimes not the exact, mathematically correct result. In the example ROUND(0.33,0.1), ROUND returns 0.3 and not 3*0.1.

If the characters "0.3" appear as a constant in a SAS program, the value is computed by the standard informat as 3/10. To be consistent with the standard informat, ROUND(0.33,0.1) computes the result as 3/10, and the following statement produces the results that you would expect.

if round(x,0.1) = 0.3 then 
   ... more SAS statements ...

However, if you use the variable Y instead of the constant 0.3, as the following statement shows, the results might be unexpected depending on how the variable Y is computed.

if round(x,0.1) = y then 
   ... more SAS statements ...

If SAS reads Y as the characters "0.3" using the standard informat, the result is the same as if a constant 0.3 appeared in the IF statement. If SAS reads Y with a different informat, or if a program other than SAS reads Y, then there is no guarantee that the characters "0.3" would produce a value of exactly 3/10. Imprecision can also be caused by computation involving numbers that do not have exact binary representations, or by porting data sets from one operating environment to another that has a different floating-point representation.

If you know that Y is a decimal number with one decimal place, but are not certain that Y has exactly the same value as would be produced by the standard informat, it is better to use the following statement:

if round(x,0.1) = round(y,0.1) then 
   ... more SAS statements ...

You should not use the ROUND function as a general method to test for approximate equality. Two numbers that differ only in the least significant bit can round to different values if one number rounds down and the other number rounds up. Testing for approximate equality depends on how the numbers have been computed. If both numbers are computed to high relative precision, you could test for approximate equality by using the ABS and the MAX functions, as the following example shows.

if abs(x-y) <= 1e-12 * max( abs(x), abs(y) ) then 
   ... more SAS statements ...

In general, ROUND(argument, rounding-unit) produces the result that you expect from decimal arithmetic if the result has no more than nine significant digits and any of the following conditions are true:

For example:

options pageno=1 nodate;

data rounding;
   d1 = round(1234.56789,100)     - 1200; 
   d2 = round(1234.56789,10)      - 1230; 
   d3 = round(1234.56789,1)       - 1235; 
   d4 = round(1234.56789,.1)      - 1234.6;
   d5 = round(1234.56789,.01)     - 1234.57; 
   d6 = round(1234.56789,.001)    - 1234.568;  
   d7 = round(1234.56789,.0001)   - 1234.5679; 
   d8 = round(1234.56789,.00001)  - 1234.56789;
   d9 = round(1234.56789,.1111)   - 1234.5432; 
      /* d10 has too many decimal places in the value for */
      /* rounding-unit.                                   */
   d10 = round(1234.56789,.11111) - 1234.54321; 
run;
proc print data=rounding noobs;
run;

When the rounding unit is the reciprocal of an integer, the ROUND function computes the result by dividing by the integer. (ROUND treats the rounding unit as a reciprocal of an integer if the reciprocal of the rounding unit differs from an integer in at most the three or four least significant bits.) Therefore, you can safely compare the result from ROUND with the ratio of two integers, but not with a multiple of the rounding unit. For example:

options pageno=1 nodate;

data rounding2;
   drop pi unit;
   pi = arcos(-1);
   unit=1/7;
   d1=round(pi,unit) - 22/7;        
   d2=round(pi, unit) - 22*unit;  
run;
proc print data=rounding2 noobs;
run;

The ROUND function computes the result by multiplying an integer by the rounding unit when all of the following conditions are true:

For example:

data _null_;
   difference=round(1234.56789,.11111) - 11111*.11111;
   put difference=;
run;

The following line is written to the SAS log:

   difference=0

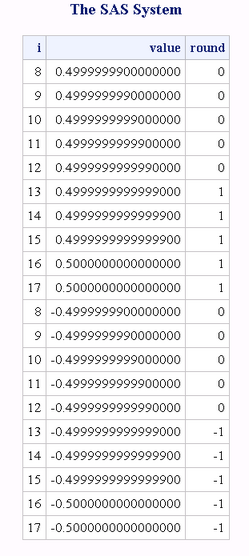
When the value to be rounded is approximately halfway between two multiples of the rounding unit, the ROUND function rounds up the absolute value and restores the original sign. For example:

data test;
   do i=8 to 17;
      value=0.5 - 10**(-i);
      round=round(value);
      output;
   end;
   do i=8 to 17;
      value=-0.5 + 10**(-i);
      round=round(value);
      output;
   end;
run;
proc print data=test noobs;
   format value 19.16;
run;

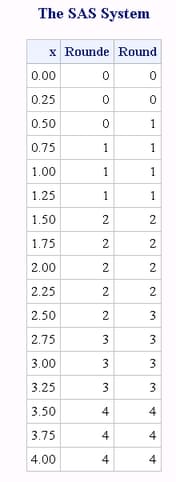
The approximation is relative to the size of the value to be rounded, and is computed in a manner that is shown in the following DATA step. This DATA step code will not always produce results exactly equivalent to the ROUND function.

data testfile;
   do i = 1 to 17;
      value = 0.5 - 10**(-i);
      epsilon = min(1e-6, value * 1e-12);
      temp = value + .5 + epsilon;
      fraction = modz(temp, 1);
      round = temp - fraction;
      output;
   end;
run;
proc print data=testfile noobs;
   format value 19.16;
run;