The following example compares the LMS and FAST-LTS subroutines. The data are the stack loss data of Brownlee (1965). The three explanatory variables correspond to measurements for a plant that oxidizes ammonia to nitric acid on 21 consecutive days:
-
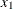 represents the air flow to the plant.
represents the air flow to the plant.
-
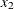 represents the temperature of cooling water.
represents the temperature of cooling water.
-
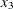 represents the acid concentration.
represents the acid concentration.
The response variable gives the permillage of ammonia lost (stack loss). The following data are also given in Rousseeuw and Leroy (1987) and Osborne (1985):
/* Obs X1 X2 X3 Y Stack Loss data */
SL = { 1 80 27 89 42,
2 80 27 88 37,
3 75 25 90 37,
4 62 24 87 28,
5 62 22 87 18,
6 62 23 87 18,
7 62 24 93 19,
8 62 24 93 20,
9 58 23 87 15,
10 58 18 80 14,
11 58 18 89 14,
12 58 17 88 13,
13 58 18 82 11,
14 58 19 93 12,
15 50 18 89 8,
16 50 18 86 7,
17 50 19 72 8,
18 50 19 79 8,
19 50 20 80 9,
20 56 20 82 15,
21 70 20 91 15 };
x = SL[, 2:4]; y = SL[, 5];
Rousseeuw and Leroy (1987) cite a large number of papers in which the preceding data were analyzed. They state that most researchers “concluded that observations 1, 3, 4, and 21 were outliers” and that some people also reported observation 2 as an outlier.
For ![]() and
and ![]() (three explanatory variables plus an intercept), there are a total of
(three explanatory variables plus an intercept), there are a total of ![]() 5,985 different subsets of four observations. If you do not specify OPTN[5], the LMS subroutine draws 2,000 random sample
subsets. A large number of subsets are collinear and therefore lead to singular linear systems. To suppress printing these
subsets and to reduce other output, choose OPTN[2]=2 as in the following statements:
5,985 different subsets of four observations. If you do not specify OPTN[5], the LMS subroutine draws 2,000 random sample
subsets. A large number of subsets are collinear and therefore lead to singular linear systems. To suppress printing these
subsets and to reduce other output, choose OPTN[2]=2 as in the following statements:
/* Use 2000 Random Subsets for LMS */ optn = j(9,1,.); optn[2]= 2; /* print a moderate amount of output */ optn[3]= 1; /* compute only LMS regression */ ods select IterHist0 BestSubset EstCoeff; call lms(sc, coef, wgt, optn, y, x); ods select all;
Summary statistics are shown in Output 12.2.1. The “IterHist0” table summarizes the process of choosing subsets of four observations. A total of 2,103 subsets are chosen in order to obtain
2,000 nonsingular subsets. The subset that yields the best regression fit consists of observations 10, 11, 15, and 19. The
parameter estimates for the LMS regression are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Output 12.2.1: LMS Regression Output
| Subset | Singular | Best Criterion |
Percent |
|---|---|---|---|
| 500 | 23 | 0.163262 | 25 |
| 1000 | 55 | 0.140519 | 50 |
| 1500 | 79 | 0.140519 | 75 |
| 2000 | 103 | 0.126467 | 100 |
| Observations of Best Subset | |||
|---|---|---|---|
| 15 | 11 | 19 | 10 |
| Estimated Coefficients | |||
|---|---|---|---|
| VAR1 | VAR2 | VAR3 | Intercep |
| 0.75 | 0.5 | 0 | -39.25 |
The three matrices that are returned by the LMS subroutine contain detailed information about the regression. A few of the results are shown in Output 12.2.2, which is produced by the following statements:
r1 = {"Quantile", "Number of Subsets", "Number of Singular Subsets",
"Number of Nonzero Weights", "Min Objective Function",
"Preliminary Scale Estimate", "Final Scale Estimate",
"Robust R Squared", "Asymptotic Consistency Factor"};
sc1 = sc[1:9];
print sc1[r=r1 L="LMS Information and Estimates"];
The matrix that is shown in Output 12.2.2 includes the following information:
-
The LMS algorithm minimizes the square of the 13th smallest residual.
-
Of the 21 observations in the data, 17 are assigned nonzero weights. Equivalently, four are classified as influential observations and are assigned zero weights.
-
The other statistics are described in the documentation for the LMS subroutine.
Output 12.2.2: LMS Regression Output
| LMS Information and Estimates | |
|---|---|
| Quantile | 13 |
| Number of Subsets | 2103 |
| Number of Singular Subsets | 103 |
| Number of Nonzero Weights | 17 |
| Min Objective Function | 0.75 |
| Preliminary Scale Estimate | 1.0478511 |
| Final Scale Estimate | 1.2076147 |
| Robust R Squared | 0.9648438 |
| Asymptotic Consistency Factor | 1.1413664 |
You can print the wgt vector to discover that the observations 1, 3, 4, and 21 have scaled residuals larger than 2.5 (output not shown) and so
are classified as outliers.
The FAST-LTS algorithm uses only 500 random subsets and gets better optimization results, as measured by the sum of the squared residuals criterion. The following statements call the LTS subroutine:
/* Use 500 random subsets for FAST-LTS algorithm */ optn = j(9,1,.); optn[2]= 0; /* suppress output */ optn[3]= 0; /* compute only LTS regression */ optn[9]= 0; /* FAST-LTS */ call lts(sc, coef, wgt, optn, y, x);
The following statements display information about the LTS algorithm, parameter estimates, and outliers:
r1 = {"Quantile", "Number of Subsets", "Number of Singular Subsets",
"Number of Nonzero Weights", "Min Objective Function",
"Preliminary Scale Estimate", "Final Scale Estimate",
"Robust R Squared", "Asymptotic Consistency Factor"};
sc1 = sc[1:9];
print sc1[r=r1 L="LTS Information and Estimates"];
print (coef[1,])[L="Estimated Coefficients"
c={"x1" "x2" "x3" "Intercept"}];
outliers = loc(wgt[1,]=0);
print outliers;
The results are shown in Output 12.2.3. The LTS algorithm examines 517 subsets of observations, for which 17 are singular, and classifies six observations as outliers. The output also shows the parameter estimates for the regression model.
Output 12.2.3: Results for LTS Algorithm
| LTS Information and Estimates | |
|---|---|
| Quantile | 13 |
| Number of Subsets | 517 |
| Number of Singular Subsets | 17 |
| Number of Nonzero Weights | 15 |
| Min Objective Function | 0.4749406 |
| Preliminary Scale Estimate | 0.9888436 |
| Final Scale Estimate | 1.0360273 |
| Robust R Squared | 0.974552 |
| Asymptotic Consistency Factor | 2.0820364 |
| Estimated Coefficients | |||
|---|---|---|---|
| x1 | x2 | x3 | Intercept |
| 0.7409211 | 0.3915267 | 0.0111345 | -37.32333 |
| outliers | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 13 | 21 |
For a small number of observations, you can generate regression results by considering all possible subsets of observations.
For the LMS subroutine, you can set OPTN[5] = ![]() to generate all subsets. For the stack loss data, the parameter estimates are identical to Output 12.2.2.
to generate all subsets. For the stack loss data, the parameter estimates are identical to Output 12.2.2.