LMS Call :: SAS/IML(R) 13.1 User's Guide

LMS Call

Subsections:

Example

CALL LMS (sc, coef, wgt, opt, y <*>, x <*>, sorb ) ;

The LMS subroutine performs least median of squares (LMS) robust regression (sometimes called resistant regression) by minimizing the $h$ th-ordered squared residual. The subroutine is able to detect outliers and perform a least squares regression on the remaining observations.

The algorithm used in the LMS subroutine is based on the PROGRESS program of Rousseeuw and Hubert (1996), which is an updated version of Rousseeuw and Leroy (1987). In the special case of regression through the origin with a single regressor, Barreto and Maharry (2006) show that the PROGRESS algorithm does not, in general, find the slope that yields the least median of squares. Starting with SAS/IML 9.2, the LMS subroutine uses the algorithm of Barreto and Maharry (2006) to obtain the correct LMS slope in the case of regression through the origin with a single regressor. In this case, input arguments that are specific to the PROGRESS algorithm are ignored and output specific to the PROGRESS algorithm is suppressed.

The value of $h$ can be specified, but in most applications the default value works well and the results seem to be quite stable toward different choices of $h$ .

In the following discussion, $N$ is the number of observations and $n$ is the number of regressors. The input arguments to the LMS subroutine are as follows:

opt

specifies an options vector. The options vector can be a vector of missing values, which results in default values for all options. The components of opt are as follows:

opt[1]

specifies whether an intercept is used in the model (opt[1]=0) or not (opt[1] 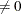$\neq 0$ ). If opt[1]=0, then a column of ones is added as the last column to the input matrix 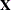$\mb {X}$ ; that is, you do not need to add this column of ones yourself. The default is opt[1]=0.

opt[2]

specifies the amount of printed output. Higher values request additional output and include the output of lower values.

0: prints no output except error messages.
1: prints all output except (1) arrays of 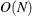$O(N)$ , such as weights, residuals, and diagnostics; (2) the history of the optimization process; and (3) subsets that result in singular linear systems.
2: additionally prints arrays of 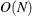$O(N)$ , such as weights, residuals, and diagnostics; also prints the case numbers of the observations in the best subset and some basic history of the optimization process.
3: additionally prints subsets that result in singular linear systems.

The default is opt[2]=0.

opt[3]

specifies whether only LMS is computed or whether, additionally, least squares (LS) and weighted least squares (WLS) regression are computed.

0: computes only LMS.
1: computes, in addition to LMS, weighted least squares regression on the observations with small LMS residuals (where small is defined by opt[8]).
2: computes, in addition to LMS, unweighted least squares regression.
3: adds both unweighted and weighted least squares regression to LMS regression.

The default is opt[3]=0.

opt[4]

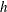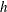specifies the quantile $h$ to be minimized. This is used in the objective function. The default is opt[4] $=h=\left[\frac{N+n+1}{2}\right]$ , which corresponds to the highest possible breakdown value. This is also the default of the PROGRESS program. The value of $h$ should be in the range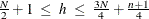 $\frac{N}{2}+1 ~ \leq ~ h ~ \leq ~ \frac{3N}{4} + \frac{n+1}{4}$

opt[5]

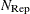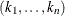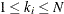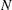specifies the number $N_\mr {Rep}$ of generated subsets. Each subset consists of $n$ observations $(k_1,\ldots ,k_ n)$ , where $1 \leq k_ i \leq N$ . The total number of subsets that contain $n$ observations out of $N$ observations is

$N_\mr {tot} = {N \choose n} = \frac{\prod _{j=1}^ n (N-j+1)}{\prod _{j=1}^ n j}$

where $n$ is the number of parameters including the intercept.

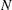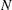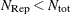Due to computer time restrictions, not all subset combinations of $n$ observations out of $N$ can be inspected for larger values of $N$ and $n$ . Specifying a value of $N_\mr {Rep} < N_\mr {tot}$ enables you to save computer time at the expense of computing a suboptimal solution.

If opt[5] is zero or missing, the default number of subsets is taken from the following table.

n	1	2	3	4	5	6	7	8	9	10
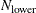
$N_\mr {lower}$	500	50	22	17	15	14	0	0	0	0
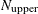
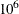
$N_\mr {upper}$	$10^6$	1414	182	71	43	32	27	24	23	22
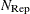
$N_\mr {Rep}$	500	1000	1500	2000	2500	3000	3000	3000	3000	3000

n	11	12	13	14	15
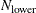
$N_\mr {lower}$	0	0	0	0	0
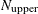
$N_\mr {upper}$	22	22	22	23	23
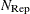
$N_\mr {Rep}$	3000	3000	3000	3000	3000

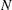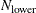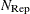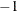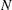If the number of cases (observations) $N$ is smaller than $N_\mr {lower}$ , then all possible subsets are used; otherwise, $N_\mr {Rep}$ subsets are chosen randomly. This means that an exhaustive search is performed for opt[5]= $-1$ . If $N$ is larger than 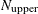$N_\mr {upper}$ , a note is printed in the log file that indicates how many subsets exist.

opt[6]

is not used.

opt[7]

specifies whether the last argument sorb contains a given parameter vector 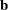$\mb {b}$ or a given subset for which the objective function should be evaluated.

0

sorb contains a given subset index.

1

sorb contains a given parameter vector $\mb {b}$ .

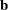The default is opt[7]=0.

opt[8]

is relevant only for LS and WLS regression (opt[3] > 0). It specifies whether the covariance matrix of parameter estimates and approximate standard errors (ASEs) are computed and printed.

0: does not compute covariance matrix and ASEs.
1: computes covariance matrix and ASEs but prints neither of them.
2: computes the covariance matrix and ASEs but prints only the ASEs.
3: computes and prints both the covariance matrix and the ASEs.

The default is opt[8]=0.

y

refers to an 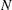$N$ response vector.

x

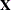refers to an $N \times n$ matrix $\mb {X}$ of regressors. If opt[1] is zero or missing, an intercept 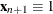$\mb {x}_{n+1} \equiv 1$ is added by default as the last column of 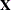$\mb {X}$ . If the matrix 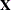$\mb {X}$ is not specified, 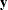$\mb {y}$ is analyzed as a univariate data set.

sorb

refers to an $n$ vector that contains either of the following:

$n$ observation numbers of a subset for which the objective function should be evaluated; this subset can be the start for a pairwise exchange algorithm if opt[7] is specified.
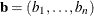$n$ given parameters $\mb {b}=(b_1,\ldots ,b_ n)$ (including the intercept, if necessary) for which the objective function should be evaluated.

Missing values are not permitted in $x$ or $y$ . Missing values in opt cause the default value to be used.

The LMS subroutine returns the following values:

sc

is a column vector that contains the following scalar information, where rows 1–9 correspond to LMS regression and rows 11–14 correspond to either LS or WLS:

sc[1]: the quantile 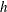$h$ used in the objective function
sc[2]: number of subsets generated
sc[3]: number of subsets with singular linear systems
sc[4]: number of nonzero weights $w_ i$
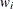
sc[5]: lowest value of the objective function 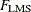$F_\mr {LMS}$ attained
sc[6]: preliminary LMS scale estimate $S_ P$
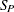
sc[7]: final LMS scale estimate $S_ F$
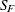
sc[8]: robust R square (coefficient of determination)
sc[9]: asymptotic consistency factor

If opt[3] > 0, then the following are also set:

sc[11]: LS or WLS objective function (sum of squared residuals)
sc[12]: LS or WLS scale estimate
sc[13]: R square value for LS or WLS
sc[14]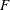: $F$ value for LS or WLS

For opt[3]=1 or opt[3]=3, these rows correspond to WLS estimates; for opt[3]=2, these rows correspond to LS estimates.

coef

is a matrix with $n$ columns that contains the following results in its rows:

coef[1,]: LMS parameter estimates
coef[2,]: indices of observations in the best subset

If opt[3] > 0, then the following are also set:

coef[3,]: LS or WLS parameter estimates
coef[4,]: approximate standard errors of LS or WLS estimates
coef[5,]: $t$ values
coef[6,]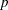: $p$ -values
coef[7,]: lower boundary of Wald confidence intervals
coef[8,]: upper boundary of Wald confidence intervals

For opt[3]=1 or opt[3]=3, these rows correspond to WLS estimates; for opt[3]=2, these rows correspond to LS estimates.

wgt

is a matrix with 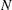$N$ columns that contains the following results in its rows:

wgt[1,]: weights (1 for small residuals; 0 for large residuals)
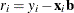
wgt[2,]: residuals $r_ i = y_ i - \mb {x}_ i \mb {b}$
wgt[3,]: resistant diagnostic 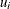$u_ i$ (the resistant diagnostic cannot be computed for a perfect fit when the objective function is zero or nearly zero)

Example

Consider results for Brownlee (1965) stackloss data. The three explanatory variables correspond to measurements for a plant that oxidizes ammonia to nitric acid on 21 consecutive days.

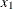$x_1$ air flow to the plant
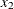$x_2$ cooling water inlet temperature
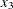$x_3$ acid concentration

The response variable $y_ i$ contains the permillage of ammonia lost (stackloss). The data are also given by Rousseeuw and Leroy (1987) and Osborne (1985). Rousseeuw and Leroy (1987) cite a large number of papers where this data set was analyzed and state that most researchers “concluded that observations 1, 3, 4, and 21 were outliers,” and that some people also reported observation 2 as an outlier.

For $N=21$ and $n=4$ (three explanatory variables including intercept), you obtain a total of 5,985 different subsets of 4 observations out of 21. If you decide not to specify opt[5], the LMS subroutine chooses $N_{rep}=$ 2,000 random sample subsets. Since there is a large number of subsets with singular linear systems, which you do not want to print, choose opt[2]=2 for reduced printed output.

   /* X1  X2  X3   Y  Stackloss data */
aa = { 1  80  27  89  42,
       1  80  27  88  37,
       1  75  25  90  37,
       1  62  24  87  28,
       1  62  22  87  18,
       1  62  23  87  18,
       1  62  24  93  19,
       1  62  24  93  20,
       1  58  23  87  15,
       1  58  18  80  14,
       1  58  18  89  14,
       1  58  17  88  13,
       1  58  18  82  11,
       1  58  19  93  12,
       1  50  18  89   8,
       1  50  18  86   7,
       1  50  19  72   8,
       1  50  19  79   8,
       1  50  20  80   9,
       1  56  20  82  15,
       1  70  20  91  15 };

a = aa[, 2:4]; b = aa[, 5];
opt = j(8, 1, .);
opt[2]= 2;    /* ipri */
opt[3]= 3;    /* ilsq */
opt[8]= 3;    /* icov */

call lms(sc, coef, wgt, opt, b, a);

The first portion of the output displays descriptive statistics, as shown in Figure 24.191:

Figure 24.191: Descriptive Statistics

LMS: The 13th ordered squared residual will be minimized.

Median and Mean
	Median	Mean
VAR1	58	60.428571429
VAR2	20	21.095238095
VAR3	87	86.285714286
Intercep	1	1
Response	15	17.523809524

Dispersion and Standard Deviation
	Dispersion	StdDev
VAR1	5.930408874	9.1682682584
VAR2	2.965204437	3.160771455
VAR3	4.4478066555	5.3585712381
Intercep	0	0
Response	5.930408874	10.171622524

The next portion of the output shows the least squares estimates and the covariance of the estimates. Information about the residuals are also displayed, but are not shown in Figure 24.192.

Figure 24.192: Least Squares Estimates

Unweighted Least-Squares Estimation

LS Parameter Estimates
Variable	Estimate	Approx Std Err	t Value	Pr > \|t\|	Lower WCI	Upper WCI
VAR1	0.7156402	0.13485819	5.31	<.0001	0.45132301	0.97995739
VAR2	1.29528612	0.36802427	3.52	0.0026	0.57397182	2.01660043
VAR3	-0.1521225	0.15629404	-0.97	0.3440	-0.4584532	0.15420818
Intercep	-39.919674	11.8959969	-3.36	0.0038	-63.2354	-16.603949

Sum of Squares = 178.8299616

Degrees of Freedom = 17

LS Scale Estimate = 3.2433639182

Cov Matrix of Parameter Estimates
	VAR1	VAR2	VAR3	Intercep
VAR1	0.0181867302	-0.036510675	-0.007143521	0.2875871057
VAR2	-0.036510675	0.1354418598	0.0000104768	-0.651794369
VAR3	-0.007143521	0.0000104768	0.024427828	-1.676320797
Intercep	0.2875871057	-0.651794369	-1.676320797	141.51474107

R-squared = 0.9135769045

F(3,17) Statistic = 59.9022259

Probability = 3.0163272E-9

The LMS subroutine prints results for the 2,000 random subsets. Figure 24.193 shows the iteration history, the best subset of observations that are used to form estimates, and the estimated parameters. The subroutine also displays residual information (not shown).

Figure 24.193: Least Median Squares Estimates

There are 5985 subsets of 4 cases out of 21 cases.

The algorithm will draw 2000 random subsets of 4 cases.

Random Subsampling for LMS

Subset	Singular	Best Criterion	Percent
500	23	0.163262	25
1000	55	0.140519	50
1500	79	0.140519	75
2000	103	0.126467	100

Minimum Criterion= 0.1264668282

Least Median of Squares (LMS) Method

Minimizing 13th Ordered Squared Residual.

Highest Possible Breakdown Value = 42.86 %

Random Selection of 2103 Subsets

Among 2103 subsets 103 is/are singular.

Observations of Best Subset
15	11	19	10

Estimated Coefficients
VAR1	VAR2	VAR3	Intercep
0.75	0.5	0	-39.25

Observations 1, 3, 4, and 21 have scaled residuals larger than 2.0 (table not shown) and are considered outliers. The corresponding WLS estimates are shown in Figure 24.194:

Figure 24.194: Weighted Least Squares Estimates

LMS Objective Function = 0.75

Preliminary LMS Scale = 1.0478510755

Robust R Squared = 0.96484375

Final LMS Scale = 1.2076147288

LMS Residuals
N	Observed	Estimated	Residual	Res / S
1	42.000000	34.250000	7.750000	6.417610
2	37.000000	34.250000	2.750000	2.277216
3	37.000000	29.500000	7.500000	6.210590
4	28.000000	19.250000	8.750000	7.245688
5	18.000000	18.250000	-0.250000	-0.207020
6	18.000000	18.750000	-0.750000	-0.621059
7	19.000000	19.250000	-0.250000	-0.207020
8	20.000000	19.250000	0.750000	0.621059
9	15.000000	15.750000	-0.750000	-0.621059
10	14.000000	13.250000	0.750000	0.621059
11	14.000000	13.250000	0.750000	0.621059
12	13.000000	12.750000	0.250000	0.207020
13	11.000000	13.250000	-2.250000	-1.863177
14	12.000000	13.750000	-1.750000	-1.449138
15	8.000000	7.250000	0.750000	0.621059
16	7.000000	7.250000	-0.250000	-0.207020
17	8.000000	7.750000	0.250000	0.207020
18	8.000000	7.750000	0.250000	0.207020
19	9.000000	8.250000	0.750000	0.621059
20	15.000000	12.750000	2.250000	1.863177
21	15.000000	23.250000	-8.250000	-6.831649

Distribution of Residuals

MinRes	1st Qu.	Median	Mean	3rd Qu.	MaxRes
-8.25	-0.5	0.25	0.9047619048	0.75	8.75

Resistant Diagnostic
N	U	Resistant Diagnostic
1	10.448052	2.278040
2	7.931751	1.729399
3	10.000000	2.180349
4	11.666667	2.543741
5	2.729730	0.595176
6	3.486486	0.760176
7	4.729730	1.031246
8	4.243243	0.925175
9	3.648649	0.795533
10	3.759835	0.819775
11	4.605767	1.004218
12	4.925169	1.073859
13	3.888889	0.847914
14	4.586421	1.000000
15	5.297030	1.154938
16	4.009901	0.874299
17	6.679576	1.456381
18	4.305340	0.938715
19	4.019976	0.876495
20	3.000000	0.654105
21	11.000000	2.398384

Median(U)= 4.5864208797

Weighted Least-Squares Estimation

RLS Parameter Estimates Based on LMS
Variable	Estimate	Approx Std Err	t Value	Pr > \|t\|	Lower WCI	Upper WCI
VAR1	0.79768556	0.06743906	11.83	<.0001	0.66550742	0.9298637
VAR2	0.57734046	0.16596894	3.48	0.0041	0.25204731	0.9026336
VAR3	-0.0670602	0.06160314	-1.09	0.2961	-0.1878001	0.05367975
Intercep	-37.652459	4.73205086	-7.96	<.0001	-46.927108	-28.37781

Weighted Sum of Squares = 20.400800254

Degrees of Freedom = 13

RLS Scale Estimate = 1.2527139846

Cov Matrix of Parameter Estimates
	VAR1	VAR2	VAR3	Intercep
VAR1	0.0045480273	-0.007921409	-0.001198689	0.0015681747
VAR2	-0.007921409	0.0275456893	-0.00046339	-0.065017508
VAR3	-0.001198689	-0.00046339	0.0037949466	-0.246102248
Intercep	0.0015681747	-0.065017508	-0.246102248	22.392305355

Weighted R-squared = 0.9750062263

F(3,13) Statistic = 169.04317954

Probability = 1.158521E-10

There are 17 points with nonzero weight.

Average Weight = 0.8095238095