REGRESS Call :: SAS/IML(R) 13.1 User's Guide

REGRESS Call

RUN REGRESS (x, y, name, <tval>, <l1>, <l2>, <l3>) ;

The REGRESS module performs ordinary least squares regression. It is primarily used for demonstration purposes.

The inputs to the REGRESS subroutine are as follows:

x: is an 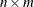$n \times m$ numeric matrix, where 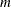$m$ is the number of variables and $n$ is the number of data points.
y: is an 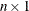$n \times 1$ response vector.
name: is an 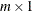$m \times 1$ matrix of variable names.
tval: is an optional $t$ -value.
l1, l2, l3: are optional 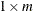$1 \times m$ vectors that specify linear combinations of coefficients for hypothesis testing.

The design matrix is given by x, and y is the response vector. The name vector identifies each of the variables. If you specify a $t$ -value, the module prints a table of observed and predicted values, residuals, hat diagonal, and confidence limits for the mean and predicted values. If you also specify linear combinations with l1, l2, and l3, the module performs the hypothesis test $\mb {H:} ~ l^{\prime }b = 0$ , where $b$ is the vector of parameter estimates. An example follows:

/* U.S. Population for decades beginning 1790, in millions */
name = { "Intercept", "Decade", "Decade**2" };
x = { 1  1  1,   1  2  4,   1  3  9,   1  4 16,
      1  5 25,   1  6 36,   1  7 49,   1  8 64 };
y = {  3.929,    5.308,     7.239,     9.638,
      12.866,   17.069,    23.191,    31.443 };
/* 5 dof at 0.025 level to get 95% confidence interval */
tval = quantile("T", 1-0.025, 5);
l1 = { 0 1 0 };   /* test hypothesis lb=0 for linear coef */
l2 = { 0 1 0,     /* test hypothesis lb=0 for linear,quad */
       0 0 1 };
l3 = { 0 1 1 };   /* test hypothesis lb=0 for linear+quad */
run regress( x, y, name, tval, l1, l2, l3 );

Figure 25.2: Regression Analysis

name	b	stdb	t	probt
Intercept	5.0693393	0.9655939	5.2499702	0.0033263
Decade	-1.109935	0.4923003	-2.254588	0.0738509
Decade**2	0.5396369	0.0533975	10.10604	0.0001625

Covariance of Estimates
	Intercept	Decade	Decade**2
Intercept	0.9324	-0.436	0.0428
Decade	-0.436	0.2424	-0.026
Decade**2	0.0428	-0.026	0.0029

Correlation of Estimates
	Intercept	Decade	Decade**2
Intercept	1	-0.918	0.8295
Decade	-0.918	1	-0.976
Decade**2	0.8295	-0.976	1

Predicted values, Residuals, and Limits

y	yhat	resid	h	lowerm	upperm	lower	upper
3.929	4.499	-0.57	0.7083	3.0017	5.9964	2.1737	6.8244
5.308	5.008	0.3	0.2798	4.067	5.949	2.9954	7.0207
7.239	6.5963	0.6427	0.2321	5.7391	7.4535	4.6214	8.5711
9.638	9.2638	0.3742	0.2798	8.3228	10.205	7.2511	11.276
12.866	13.011	-0.145	0.2798	12.07	13.952	10.998	15.023
17.069	17.837	-0.768	0.2321	16.979	18.694	15.862	19.812
23.191	23.742	-0.551	0.2798	22.801	24.683	21.729	25.755
31.443	30.727	0.7164	0.7083	29.229	32.224	28.401	33.052

Test Hypothesis that l b = 0

	f	dfn	dfe	prob
for Linear Coef	5.0831686	1	5	0.0739

	f	dfn	dfe	prob
for Linear,Quad Coef	666.51095	2	5	<.0001

	f	dfn	dfe	prob
for Linear+Quad Coef	1.6774629	1	5	0.2518