The QUADREG module fits a quadratic response surface to data. It is primarily used for demonstration purposes. The inputs to the QUADREG subroutine are as follows:
- xopt
-
is a returned value that contains
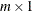 critical factor values.
critical factor values.
- yopt
-
is a returned value that contains the critical response value.
- type
-
is a returned character string that contains the solution type (maximum or minimum).
- parms
-
is a returned value that contains the parameter estimates for the quadratic model.

-
is an
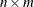 data matrix, where
data matrix, where 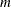 is the number of factor variables and
is the number of factor variables and  is the number of data points.
is the number of data points.
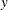
-
is an
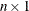 response vector.
response vector.
The QUADREG module fits a regression model with a complete quadratic set of regressions across several factors. The estimated model parameters are divided into a vector of linear coefficients and a matrix of quadratic coefficients to obtain critical factor values that optimize the response. It further determines the type of the optima (maximum, minimum, or saddle point) by computing the eigenvalues of the estimated parameters.
x = { -1 -1, -1 0, -1 1, 0 -1,
0 0, 0 1, 1 -1, 1 0, 1 1 };
y = { 71.7, 75.2, 76.3, 79.2, 81.5, 80.2, 80.1, 79.1, 75.8 };
run quadreg( xopt, yopt, nature, parms, x, y );
print parms[rowname={c b1 b2 a11 a12 a22} label="Parameter Estimates"],
xopt[rowname={x1 x2} label="Critical Factor Values"],
nature[label=""] "Response" yopt [label=""];
Figure 25.1: Parameter Estimates and Optima
| Parameter Estimates | |
|---|---|
| C | 81.222222 |
| B1 | 1.9666667 |
| B2 | 0.2166667 |
| A11 | -3.933333 |
| A12 | -2.225 |
| A22 | -1.383333 |
| Critical Factor Values |
|
|---|---|
| X1 | 0.2949376 |
| X2 | -0.158881 |
| Maximum | Response | 81.495032 |