WAVIFT Call :: SAS/IML(R) 13.1 User's Guide

WAVIFT Call

CALL WAVIFT (result, decomp <, opt> <, level> ) ;

The Inverse Fast Wavelet Transform (WAVIFT) subroutine computes the inverse wavelet transform of a wavelet decomposition computed by using the WAVFT subroutine. Details of this algorithm are available in many references, including Mallat (1989), Daubechies (1992), and Ogden (1997).

The inverse transform yields an exact reconstruction of the original input data, provided that no smoothing is specified. Alternatively, a smooth reconstruction of the input data can be obtained by thresholding the detail coefficients in the decomposition prior to applying the inverse transformation. Thresholding, also known as shrinkage, replaces the detail coefficient $d_ j^{(i)}$ at level $i$ by $\delta _{T_ i} ( d_ j^{(i)} )$ , where the $\delta _ T(x)$ is a shrinkage function and $T_ i$ is the threshold value used at level $i$ . The wavelet subroutines support hard and soft shrinkage functions (Donoho and Johnstone, 1994) and the nonnegative garrote shrinkage function (Breiman, 1995). These functions are defined as follows:

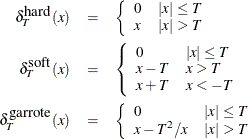
$\begin{eqnarray*} \delta _ T^{\mbox{hard}} (x) & = & \left\{ \begin{array}{ll} 0 & |x| \leq T \\ x & |x| > T \end{array} \right. \\ \delta _ T^{\mbox{soft}} (x) & = & \left\{ \begin{array}{ll} 0 & |x| \leq T \\ x-T & x > T \\ x+T & x < -T \end{array} \right. \\ \delta _ T^{\mbox{garrote}} (x) & = & \left\{ \begin{array}{ll} 0 & |x| \leq T \\ x-T^2/x & |x| > T \end{array} \right. \end{eqnarray*}$

You can specify several methods for choosing the threshold values. Methods in which the threshold $T_ i$ varies with the level $i$ are called adaptive. Methods where the same threshold is used at all levels are called global.

The input arguments to the WAVIFT subroutine are as follows:

decomp

specifies a wavelet decomposition that has been computed by using a call to the WAVFT subroutine.

opt

refers to an options vector that specifies the thresholding algorithm. If this optional argument is not specified, then no thresholding is applied.

The options vector has the following components:

opt[1]

specifies the thresholding policy.

0: specifies that no thresholding be done. If opt[1]=0 then all other entries in the options vector are ignored.
1: specifies hard thresholding.
2: specifies soft thresholding.
3: specifies garrote thresholding.

opt[2]

specifies the method for selecting the threshold.

0: specifies a global user-supplied threshold.
1: specifies a global threshold chosen by using the minimax criterion of Donoho and Johnstone (1994).
2: specifies a global threshold defined by using the universal criterion of Donoho and Johnstone (1994).
3: specifies an adaptive method where the thresholds at each level 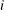$i$ are chosen to minimize an approximation of the 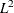$L^2$ risk in estimating the true data values by using the reconstruction with thresholded coefficients (Donoho and Johnstone, 1995).
4: specifies a hybrid method of Donoho and Johnstone (1995). The universal threshold as specified by opt[2]=2 is used at levels where most of the detail coefficients are essentially zero. The risk minimization method as specified by opt[2]=4 is used at all other levels.

opt[3]

specifies the value of the global user-supplied threshold if opt[2]=1. It is ignored if opt[2] ${\neq 1}$ .

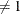opt[4]

specifies the number of levels starting at the highest detail coefficient level at which thresholding is to be applied. If this value is negative or missing, thresholding is applied at all levels in decomp.

Some common examples of threshold options specifications are:

opt={1 3 . -1};: specifies hard thresholding with a minimax threshold applied at all levels in the decomposition. This threshold is named “RiskShrink” in Donoho and Johnstone (1994).
opt={2 2 . -1};: specifies soft thresholding with a universal threshold applied at all levels in the decomposition. This threshold is named “VisuShrink” in Donoho and Johnstone (1994).
opt={2 4 . -1};: specifies soft thresholding with level dependent thresholds which minimize the Stein Unbiased Estimate of Risk (SURE). This threshold is named “SureShrink” in Donoho and Johnstone (1995).

level

is an optional scalar argument that specifies the level at which the reconstructed data are to be returned. If this argument is not specified then the reconstructed data are returned at the top level defined in decomp.

The WAVIFT subroutine returns

result: a vector obtained by inverting, after thresholding the detail coefficients, the discrete wavelet transform encoded in decomp. The row or column orientation of result is the same as that of the input data specified in the corresponding WAVFT subroutine. If you specify the optional level argument, result contains the reconstruction at the specified level, otherwise the reconstruction corresponds to the top level in the decomposition.

An example is available in the documentation for the WAVFT subroutine.