SVD Call :: SAS/IML(R) 13.1 User's Guide

Previous Page|Next Page

SVD Call

CALL SVD (u, q, v, a) ;

The SVD subroutine computes the singular value decomposition for a numerical matrix.

The input to the SVD subroutine is as follows:

a

is the $m \times n$ input matrix that is factored as described in the following discussion.

The SVD subroutine returns the following output arguments:

u

is an $m \times n$ orthonormal matrix

q

is an 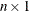$n\times 1$ vector that contains the singular values

v

is an 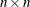$n \times n$ orthonormal matrix

If $m \geq n$ , the SVD subroutine factors a real $m \times n$ matrix $\mb {A}$ into the form

$\mb {A}= \mb {U} \mbox{diag}(\mb {Q}) \mb {V}^{\prime }$

where

$\mb {U}^{\prime } \mb {U} = \mb {V}^{\prime } \mb {V} = \mb {VV}^{\prime } = \mb {I}_ n$

and $\mb {Q}$ contains the singular values of $\mb {A}$ . The columns of $\mb {U}$ contains of the orthonormal eigenvectors of $\mb {AA}^{\prime }$ , and $\mb {V}$ contains the orthonormal eigenvectors of $\mb {A}^{\prime } \mb {A}$ . $\mb {Q}$ contains the square roots of the eigenvalues of $\mb {A}^{\prime } \mb {A}$ and $\mb {AA}^{\prime }$ , except for some zeros.

If $m<n$ , a corresponding decomposition is done where $\mb {U}$ and $\mb {V}$ switch roles:

$\mb {A}= \mb {U} \mbox{diag}(\mb {Q}) \mb {V}^{\prime }$

where

$\mb {U}^{\prime } \mb {U} = \mb {UU}^{\prime } = \mb {V}^{\prime } \mb {V} = \mb {I}_ w$

The singular values are sorted in descending order.

For information about the method used in the SVD subroutine, see Wilkinson and Reinsch (1971).

The following example is taken from Wilkinson and Reinsch (1971):

a = {22  10   2   3   7,
     14   7  10   0   8,
     -1  13  -1 -11   3,
     -3  -2  13  -2   4,
      9   8   1  -2   4,
      9   1  -7   5  -1,
      2  -6   6   5   1,
      4   5   0  -2   2};
call svd(u, q, v, a);
print u, q, v;

/* check correctness of factors */
zero = ssq(a - u*diag(q)*v`);
reset fuzz;           /* print small numbers as zero */
print zero;

The matrix is rank-3 with exact singular values $\sqrt {1248}$ , $20$ , $\sqrt {384}$ , $0$ , and $0$ . Because of the repeated singular values, the last two columns of the $\mb {U}$ matrix are not uniquely determined. A valid result is shown in Figure 24.403:

Figure 24.403: Singular Value Decomposition

u
0.7071068	0.1581139	-0.176777	-0.328209	-0.328056
0.5303301	0.1581139	0.3535534	0.5309976	0.0489362
0.1767767	-0.790569	0.1767767	-0.413567	0.1307398
0	0.1581139	0.7071068	-0.266418	0.0321656
0.3535534	-0.158114	0	0.0253566	-0.041441
0.1767767	0.1581139	-0.53033	-0.19666	0.3666144
0	0.4743416	0.1767767	-0.500944	0.4145131
0.1767767	-0.158114	0	0.2793571	0.7509412

q
35.327043
20
19.595918
1.1E-15
5.501E-16

v
0.8006408	0.3162278	-0.288675	-0.419095	0
0.4803845	-0.632456	0	0.4405091	0.4185481
0.1601282	0.3162278	0.8660254	-0.052005	0.3487901
0	0.6324555	-0.288675	0.6760591	0.244153
0.3202563	0	0.2886751	0.4129773	-0.802217

zero
0

The SVD routine performs most of its computations in the memory allocated for returning the singular value decomposition.