The RANDWISHART function is part of the IMLMLIB library. The RANDWISHART function returns an ![]() matrix that contains
matrix that contains ![]() random draws from the Wishart distribution with DF degrees of freedom. Each row of the returned matrix represents a
random draws from the Wishart distribution with DF degrees of freedom. Each row of the returned matrix represents a ![]() matrix.
matrix.
The inputs are as follows:
- N
-
is the number of desired observations sampled from the distribution.
- DF
-
is a scalar value that represents the degrees of freedom,
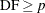 .
.
- Sigma
-
is a
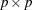 symmetric positive definite matrix.
symmetric positive definite matrix.
The Wishart distribution is a multivariate generalization of the gamma distribution. (Note, however, that Kotz, Balakrishnan, and Johnson (2000) suggest that the term “multivariate gamma distribution” should be restricted to those distributions for which the marginal distributions are univariate gamma. This is not the case with the Wishart distribution.) A Wishart distribution is a probability distribution for nonnegative definite matrix-valued random variables. These distributions are often used to estimate covariance matrices.
If a ![]() nonnegative definite matrix
nonnegative definite matrix ![]() follows a Wishart distribution with parameters
follows a Wishart distribution with parameters ![]() degrees of freedom and a
degrees of freedom and a ![]() symmetric positive definite matrix
symmetric positive definite matrix ![]() , then
, then
-
the probability density function for
 is
is
![\[ f(x; \nu , \Sigma ) = \frac{ |x|^{(\nu -p-1)/2} \exp (-\frac{1}{2}\, \mbox{trace}(x \, \Sigma ^{-1})) }{ 2^{p \nu /2} |\Sigma |^{\nu /2} \pi ^{p(p-1)/4} \prod _{i=1}^ p \Gamma (\frac{\nu -i+1}{2})} \]](images/imlug_langref1240.png)
-
if
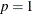 and
and 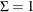 , then the Wishart distribution reduces to a chi-square distribution with
, then the Wishart distribution reduces to a chi-square distribution with  degrees of freedom.
degrees of freedom.
-
the expected value of
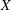 is
is 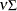 .
.
The following example generates 1,000 samples from a Wishart distribution with 7 degrees of freedom and ![]() matrix parameter
matrix parameter S. Each row of the returned matrix x represents a ![]() nonnegative definite matrix. (You can reshape the
nonnegative definite matrix. (You can reshape the ![]() th row of
th row of x with the SHAPE function.) The example computes the sample mean and compares it with the expected value.
call randseed(1);
N=1000;
DF = 7;
S = {1 1, 1 5};
x = RandWishart( N, DF, S );
Mean = DF * S;
SampleMean = shape( x[:,], 2, 2);
print SampleMean Mean;
Figure 24.303: Estimated Mean of Matrices
| SampleMean | Mean | ||
|---|---|---|---|
| 7.0518633 | 7.2402925 | 7 | 7 |
| 7.2402925 | 36.056848 | 7 | 35 |
For further details about sampling from the Wishart distribution, see Johnson (1987).