KALCVS Call :: SAS/IML(R) 13.1 User's Guide

KALCVS Call

CALL KALCVS (sm, vsm, data, a, f, b, h, var, pred, vpred <*>, un <*>, vun ) ;

The KALCVS subroutine uses backward recursions to compute the smoothed estimate $z_{t|T}$ and its covariance matrix, $P_{t|T}$ , where $T$ is the number of observations in the complete data set.

The input arguments to the KALCVS subroutine are as follows.

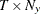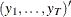data: is a $T \times N_ y$ matrix that contains data $(y_1, \ldots , y_ T)^{\prime }$ .
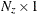a: is an $N_ z \times 1$ vector for a time-invariant input vector in the transition equation, or a 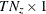$TN_ z \times 1$ vector that contains input vectors in the transition equation.
f: is an 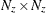$N_ z \times N_ z$ matrix for a time-invariant transition matrix in the transition equation, or a 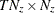$TN_ z \times N_ z$ matrix that contains 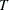$T$ transition matrices.
b: is an 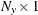$N_ y \times 1$ vector for a time-invariant input vector in the measurement equation, or a 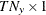$TN_ y \times 1$ vector that contains input vectors in the measurement equation.
h: is an 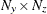$N_ y \times N_ z$ matrix for a time-invariant measurement matrix in the measurement equation, or a 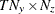$TN_ y \times N_ z$ matrix that contains 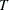$T$ time-variant 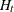$H_ t$ matrices in the measurement equation.
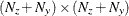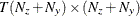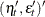var: is an $(N_ z + N_ y) \times (N_ z + N_ y)$ covariance matrix for the errors in the transition and the measurement equations, or a $T(N_ z + N_ y) \times (N_ z + N_ y)$ matrix that contains covariance matrices in the transition equation and measurement equation noises—that is, $(\eta ^{\prime }_ t, \epsilon ^{\prime }_ t)^{\prime }$ .
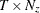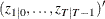pred: is a $T \times N_ z$ matrix that contains one-step forecasts $(z_{1|0}, \ldots , z_{T|T-1})^{\prime }$ .
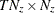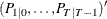vpred: is a $TN_ z \times N_ z$ matrix that contains mean square error matrices of predicted state vectors $(P_{1|0}, \ldots , P_{T|T-1})^{\prime }$ .
un: is an optional 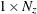$1 \times N_ z$ vector that contains 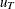$u_ T$ . The returned value is $u_0$ .
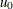vun: is an optional 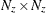$N_ z \times N_ z$ matrix that contains 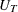$U_ T$ . The returned value is $U_0$ .

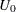The KALCVS call returns the following values:

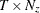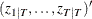sm: is a $T \times N_ z$ matrix that contains smoothed state vectors $(z_{1|T}, \ldots , z_{T|T})^{\prime }$ .
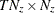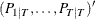vsm: is a $TN_ z \times N_ z$ matrix that contains covariance matrices of smoothed state vectors $(P_{1|T}, \ldots , P_{T|T})^{\prime }$ .

When the Kalman filtering is performed in the KALCVF call, the KALCVS call computes smoothed state vectors and their covariance matrices. The fixed-interval smoothing state vector at time $t$ is obtained by the conditional expectation given all observations.

The smoothing algorithm uses one-step forecasts and their covariance matrices, which are given in the KALCVF call. For notation, $z_{t|T}$ is the smoothed value of the state vector $z_ t$ , and the mean square error matrix is denoted $P_{t|T}$ . For smoothing,

$\begin{eqnarray*} \hat{\epsilon }_ t & = & y_ t - b_ t - H_ t z_{t|t-1} \\[0.02in] D_ t & = & H_ t P_{t|t-1} H^{\prime }_ t + R_ t \\[0.02in] K_ t & = & (F_ t P_{t|t-1} H^{\prime }_ t + G_ t) D_ t^- \\[0.02in] L_ t & = & F_ t - K_ t H_ t \\[0.02in] u_{t-1} & = & H^{\prime }_ t D_ t^- \hat{\epsilon }_ t + L^{\prime }_ t u_ t \\[0.02in] U_{t-1} & = & H^{\prime }_ t D^-_ t H_ t + L^{\prime }_ t U_ t L_ t \\[0.02in] z_{t|T} & = & z_{t|t-1} + P_{t|t-1} u_{t-1} \\[0.02in] P_{t|T} & = & P_{t|t-1} - P_{t|t-1} U_{t-1} P_{t|t-1} \end{eqnarray*}$

where $t = T, T-1, \ldots , 1$ . The initial values are $u_ T = \mb {0}$ and $\mathbf{U}_ T = \mb {0}$ .

When the SSM is specified by using the alternative transition equation

$z_ t = a_ t + F_ t z_{t-1} + \eta _ t$

the fixed-interval smoothing is performed by using the following backward recursions:

$\begin{eqnarray*} \hat{\epsilon }_ t & = & y_ t - b_ t - H_ t z_{t|t-1} \\[0.05in] D_ t & = & H_ t P_{t|t-1} H^{\prime }_ t + R_ t \\[0.05in] K_ t & = & F_{t+1} P_{t|t-1} H^{\prime }_ t D^-_ t \\[0.05in] L_ t & = & F_{t+1} - K_ tH_ t \\[0.05in] u_{t-1} & = & H^{\prime }_ t D^-_ t \hat{\epsilon }_ t + L^{\prime }_ t u_ t \\[0.05in] U_{t-1} & = & H^{\prime }_ t D^-_ t H_ t + L^{\prime }_ t U_ t L_ t \\[0.05in] z_{t|T} & = & z_{t|t-1} + P_{t|t-1} u_{t-1} \\[0.05in] P_{t|T} & = & P_{t|t-1} - P_{t|t-1} U_{t-1} P_{t|t-1} \end{eqnarray*}$

where it is assumed that $G_ t = \mb {0}$ .

You can use the KALCVS call regardless of the specification of the transition equation when $G_ t = \mb {0}$ . Harvey (1989) gives the following fixed-interval smoothing formula, which produces the same smoothed value:

$\begin{eqnarray*} z_{t|T} & = & z_{t|t} + P^*_ t (z_{t+1|T} - z_{t+1|t}) \\[0.05in] P_{t|T} & = & P_{t|t} + P^*_ t (P_{t+1|T} - P_{t+1|t}) P^{*\prime }_ t \end{eqnarray*}$

where

$P^*_ t = P_{t|t} F^{\prime }_ t P^-_{t+1|t}$

under the shifted transition equation, but

$P^*_ t = P_{t|t} F^{\prime }_{t+1} P_{t+1|t}^-$

under the alternative transition equation.

The KALCVS call is accompanied by the KALCVF call, as shown in the following statements. Note that you do not need to specify UN and VUN.

call kalcvf(pred, vpred, filt, vfilt, y, 0, a, f, b, h, var);
call kalcvs(sm, vsm, y, a, f, b, h, var, pred, vpred);

You can also compute the smoothed estimate and its covariance matrix on an observation-by-observation basis. When the SSM is time invariant, the following example performs smoothing. In this situation, you should initialize UN and VUN as matrices of value 0, as shown in the following statements:

call kalcvf(pred, vpred, filt, vfilt, y, 0, a, f, b, h, var);
n = nrow(y);
nz = ncol(f);
un = j(1, nz, 0);
vun = j(nz, nz, 0);

do i = 1 to n;
   y_i = y[n-i+1,];
   pred_i  = pred[n-i+1,];
   vpred_i = vpred[(n-i)*nz+1:(n-i+1)*nz,];
   call kalcvs(sm_i, vsm_i, y_i, a, f, b, h, var,
               pred_i, vpred_i, un, vun);
   sm  = sm_i // sm;
   vsm = vsm_i // vsm;
end;

The KALCVF call has an example program that includes the KALCVS call.