JROOT Function :: SAS/IML(R) 13.1 User's Guide

JROOT Function

JROOT (order, n) ;

The JROOT function computes the first nonzero roots of a Bessel function of the first kind and the derivative of the Bessel function at each root. The function returns an $\mbox{\Argument{n}} \times 2$ matrix with the computed roots in the first column and the derivatives in the second column. You can evaluate the Bessel function itself by calling the JBESSEL function.

The arguments to the JROOT function are as follows:

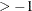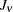order: is a scalar that denotes the order of the Bessel function, with order $> -1$ . The order of a Bessel function is often indicated with the Greek subscript $\nu$ , so that $J_{\nu }$ indicates the Bessel function of order $\nu$ .
n: is a positive integer that denotes the number of roots.

The JROOT function returns a matrix in which the first column contains the first n roots of the Bessel function; these roots are the solutions to the equation

$J_{\nu }(x_ i) = 0 , i = 1,\ldots , n$

The second column of this matrix contains the derivatives $J^{\prime }_\nu (x_ i)$ of the Bessel function at each of the roots $x_ i$ . The expression $J_\nu (x)$ is a solution to the differential equation

$x^2 \frac{d^2 J_{\nu }}{dx^2} + x \frac{dJ_{\nu }}{dx} + (x^2 - \nu ^2)J_{\nu } = 0$

One of the expressions for such a function is given by the series

$J_{\nu }(x) = \left( \frac{1}{2} z \right)^{\nu } \sum _{k=0}^{\infty } \frac{ \left( -\frac{1}{4} z^2 \right)^ k}{k! \Gamma (\nu + k + 1)}$

where $\Gamma (\cdot )$ is the gamma function. See Abramowitz and Stegun (1972) for more details concerning the Bessel and gamma functions.

The root-finding algorithm is a Newton method coupled with a reasonable initial guess. For large values of n or $\nu$ , the algorithm could fail due to machine limitations. In this case, JROOT returns a matrix with zero rows and zero columns. The values that cause the algorithm to fail are machine-dependent.

The following statements compute the first few roots for the Bessel function of the first kind:

x = jroot(1, 4);
print x;

Figure 24.179: Roots of a Bessel Function

x
3.831706	-0.402759
7.0155867	0.3001158
10.173468	-0.249705
13.323692	0.2183594

To obtain only the roots, you can use the following statement, which extracts the first column of the returned matrix:

r = x[,1];