ARMACOV Call :: SAS/IML(R) 13.1 User's Guide

ARMACOV Call

CALL ARMACOV (auto, cross, convol, phi, theta, num) ;

The ARMACOV subroutine computes an autocovariance sequence for an autoregressive moving average (ARMA) model. The input arguments to the ARMACOV subroutine are as follows:

phi: refers to a 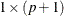$1 \times (p+1)$ matrix that contains the autoregressive parameters. The first element is assumed to have the value 1.
theta: refers to a 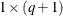$1 \times (q+1)$ matrix that contains the moving average parameters. The first element is assumed to have the value 1.
num: refers to a scalar that contains $n$ , the number of autocovariances to be computed, which must be a positive number.

The ARMACOV subroutine returns the following values:

auto: specifies a variable to contain the returned 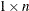$1 \times n$ matrix that contains the autocovariances of the specified ARMA model, assuming unit variance for the innovation sequence.
cross: specifies a variable to contain the returned 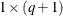$1 \times (q+1)$ matrix that contains the covariances of the moving-average term with lagged values of the process.
convol: specifies a variable to contain the returned 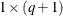$1 \times (q+1)$ matrix that contains the autocovariance sequence of the moving-average term.

The ARMACOV subroutine computes the autocovariance sequence that corresponds to a given autoregressive moving-average (ARMA) time series model. An arbitrary number of terms in the sequence can be requested. Two related covariance sequences are also returned.

The model notation for the ARMACOV subroutine is the same as for the ARMALIK subroutine. The ARMA $(p,q)$ model is denoted

$\sum _{j=0}^ p \phi _ j y_{t-j} = \sum _{i=0}^ q \theta _ i \epsilon _{t-i}$

with $\theta _0 = \phi _0 = 1$ . The notation is the same as that of Box and Jenkins (1976) except that the model parameters are opposite in sign. The innovations $\{ \epsilon _ t\}$ satisfy $E(\epsilon _ t)=0$ and $E(\epsilon _ t \epsilon _{t-k})=1$ if $k$ = 0, and are zero otherwise. The formula for the $k$ th element of the convol argument is

$\sum _{i=k-1}^ q \theta _ i \theta _{i-k+1}$

for $k=1,2,\ldots ,q+1$ . The formula for the $k$ th element of the cross argument is

$\sum _{i=k-1}^ q \theta _ i \psi _{i-k+1}$

for $k=1,2,\ldots ,q+1$ , where $\psi _ i$ is the $i$ th impulse response value. The $\psi _ i$ sequence, if desired, can be computed with the RATIO function. It can be shown that $\psi _ k$ is the same as $E(Y_{t-k} \epsilon ^2_ t)/\sigma$ , which is used by Box and Jenkins (1976) in their formulation of the autocovariances. The $k$ th autocovariance, denoted $\gamma _ k$ and returned as the $k+1$ element of the auto argument $(k=0,1,\ldots ,n-1)$ , is defined implicitly for $k>0$ by

$\sum _{i=0}^ p \gamma _{k-i} \phi _ i = \eta _ k$

where $\eta _ k$ is the $k$ th element of the cross argument. See Box and Jenkins (1976) or McLeod (1975) for more information.

Consider the model

$y_ t= 0.5y_{t-1} + e_ t + 0.8e_{t-1}$

To compute the autocovariance function at lags zero through four for this model, use the following statements:

/* an ARMA(1,1) model */
phi   = {1 -0.5};
theta = {1 0.8};
call armacov(auto, cross, convol, phi, theta, 5);
print auto, cross convol;

The result is show in Figure 24.46.

Figure 24.46: Result of the ARMACOV Subroutine

auto
3.2533333	2.4266667	1.2133333	0.6066667	0.3033333

cross		convol
2.04	0.8	1.64	0.8