| Language Reference |
NLPQUA Call
nonlinear optimization by quadratic method
- CALL NLPQUA( rc, xr, quad, x0 <,opt, blc, tc, par, "ptit", lin>);
See the section "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11 for a description of the inputs to and outputs of all NLP subroutines.
The NLPQUA subroutine uses a fast algorithm for maximizing or minimizing the quadratic objective function
The matrix
The algorithm is an active-set method in which the update of active boundary and linear constraints is done separately. The
The objective function is specified by the input arguments quad and lin, as follows:
- The quad argument specifies the symmetric
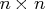 Hessian matrix,
Hessian matrix, 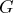 , of the quadratic term.
The input can be in dense or sparse form.
In dense form, all
, of the quadratic term.
The input can be in dense or sparse form.
In dense form, all 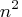 entries of the
quad matrix must be specified.
If
entries of the
quad matrix must be specified.
If 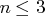 , the dense specification must be used.
The sparse specification can be useful
when
, the dense specification must be used.
The sparse specification can be useful
when 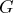 has many zero elements.
You can specify an
has many zero elements.
You can specify an 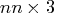 matrix in which each
row represents one of the
matrix in which each
row represents one of the 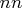 nonzero elements of
nonzero elements of 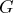 .
The first column specifies the row location in
.
The first column specifies the row location in 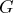 , the
second column specifies the column location, and the
third column specifies the value of the nonzero element.
, the
second column specifies the column location, and the
third column specifies the value of the nonzero element.
- The lin argument specifies the linear
part of the quadratic optimization problem.
It must be a vector of length
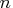 or
or 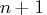 .
If lin is a vector of length
.
If lin is a vector of length 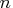 , it
specifies the vector
, it
specifies the vector 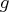 of the linear term,
and the constant term
of the linear term,
and the constant term 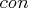 is considered zero.
If lin is a vector of length
is considered zero.
If lin is a vector of length 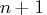 , then
the first
, then
the first 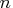 elements of the argument specify
the vector
elements of the argument specify
the vector 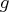 and the last element specifies the
constant term
and the last element specifies the
constant term 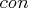 of the objective function.
of the objective function.
Assuming nonnegativity constraints
Choosing a sparse (or dense) input form of the quad argument does not mean that the algorithm used in the NLPQUA subroutine is necessarily sparse (or dense). If the following conditions are satisfied, the NLPQUA algorithm will store and process the matrix
- No general linear constraints are specified.
- The memory needed for the sparse storage of
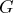 is
less than 80% of the memory needed for dense storage.
is
less than 80% of the memory needed for dense storage.
-
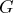 is not a diagonal matrix.
If
is not a diagonal matrix.
If 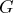 is diagonal, it is stored
and processed as a diagonal matrix.
is diagonal, it is stored
and processed as a diagonal matrix.
In addition to the standard iteration history, the NLPNRA subroutine prints the following information:
- The heading alpha is the step size,
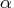 , computed with the line-search algorithm.
, computed with the line-search algorithm.
- The heading slope refers to
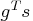 , the slope of the
search direction at the current parameter iterate
, the slope of the
search direction at the current parameter iterate 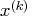 .
For minimization, this value should
be significantly smaller than zero.
Otherwise, the line-search algorithm has difficulty
reducing the function value sufficiently.
.
For minimization, this value should
be significantly smaller than zero.
Otherwise, the line-search algorithm has difficulty
reducing the function value sufficiently.
lin = { 0. 0. -100};
quad = { 0.02 0.0 ,
0.0 2.0 };
c = { 2. -50. . .,
50. 50. . .,
10. -1. 1. 10.};
x = { -1. -1.};
optn = {0 2};
CALL NLPQUA(rc,xres,quad,x,optn,c,,,,lin);
The quad argument specifies the The iteration history follows.
Optimization Start
Parameter Estimates
Gradient Lower Upper
Objective Bound Bound
N Parameter Estimate Function Constraint Constraint
1 X1 6.800000 0.136000 2.000000 50.000000
2 X2 -1.000000 -2.000000 -50.000000 50.000000
Value of Objective Function = -98.5376
Linear Constraints
1 59.00000 : 10.0000 <= + 10.0000 * X1 - 1.0000 * X2
Null Space Method of Quadratic Problem
Parameter Estimates 2
Lower Bounds 2
Upper Bounds 2
Linear Constraints 1
Using Sparse Hessian _
Optimization Start
Active Constraints 0 Objective Function -98.5376
Max Abs Gradient Element 2
Function Active Objective
Iter Restarts Calls Constraints Function
1 0 2 1 -99.87349
2 0 3 1 -99.96000
Objective Max Abs Slope of
Function Gradient Step Search
Iter Change Element Size Direction
1 1.3359 0.5882 0.706 -2.925
2 0.0865 0 1.000 -0.173
Optimization Results
Iterations 2 Function Calls 4
Gradient Calls 3 Active Constraints 1
Objective Function -99.96 Max Abs Gradient Element 0
Slope of Search Direction -0.173010381
ABSGCONV convergence criterion satisfied.
Optimization Results
Parameter Estimates
Gradient Active
Objective Bound
N Parameter Estimate Function Constraint
1 X1 2.000000 0.040000 Lower BC
2 X2 0 0
Value of Objective Function = -99.96
Linear Constraints Evaluated at Solution
1 10.00000 = -10.0000 + 10.0000 * X1 - 1.0000 * X2
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.