Language Reference: MCD Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

MCD Call

finds the minimum covariance determinant estimator

CALL MCD( sc, coef, dist, opt, );

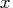The MCD call is the robust (resistant) estimation of multivariate location and scatter, defined by minimizing the determinant of the covariance matrix computed from

points. The algorithm for the MCD subroutine is based on the FAST-MCD algorithm given by Rousseeuw and Van Driessen (1999).

The MCD subroutine computes the minimum covariance determinant estimator. These robust locations and covariance matrices can be used to detect multivariate outliers and leverage points. For this purpose, the MCD subroutine provides a table of robust distances.

In the following discussion,

is the number of observations and

is the number of regressors. The inputs to the MCD subroutine are as follows:

opt

refers to an options vector with the following components (missing values are treated as default values):

opt[1]

specifies the amount of printed output. Higher option values request additional output and include the output of lower values.

opt[1]=0: prints no output except error messages.
opt[1]=1: prints most of the output.
opt[1]=2: additionally prints case numbers of the observations in the best subset and some basic history of the optimization process.
opt[1]=3: additionally prints how many subsets result in singular linear systems.

The default is opt[1]=0.

opt[2]

specifies whether the classical, initial, and final robust covariance matrices are printed. The default is opt[2]=0. Note that the final robust covariance matrix is always returned in coef.

opt[3]

specifies whether the classical, initial, and final robust correlation matrices are printed or returned:

opt[3]=0: does not return or print.
opt[3]=1: prints the robust correlation matrix.
opt[3]=2: returns the final robust correlation matrix in coef.
opt[3]=3: prints and returns the final robust correlation matrix.

opt[4]

specifies the quantile

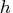used in the objective function. The default is opt[4]= $h = [\frac{n+n+1}2]$ . If the value of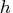

is specified outside the range 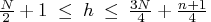$\frac{n}2+1 \leq h \leq \frac{3n}4 + \frac{n+1}4$ , it is reset to the closest boundary of this region.

opt[5]

specifies the number 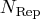$n_{\rm rep}$ of subset generations. This option is the same as described for the LTS subroutines. Due to computer time restrictions, not all subset combinations can be inspected for larger values of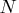

and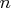

.

When opt[5] is zero or missing:

If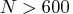 $n\gt 600$ , construct up to five disjoint random subsets with sizes as equal as possible, but not to exceed 300. Inside each subset, choose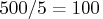

subset combinations of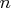

observations.

If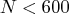 $n\lt 600$ , the number of subsets is taken from the following table.

n	1	2	3	4	5	6	7	8	9	10
$n_{\rm lower}$	500	50	22	17	15	14	0	0	0	0

n	11	12	13	14	15
$n_{\rm lower}$	0	0	0	0	0

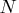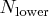: If the number of cases (observations) is smaller than $n_{\rm lower}$ , then all possible subsets are used; otherwise, 500 subsets are chosen randomly. This means that an exhaustive search is performed for opt[5]=-1. If 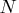is larger than 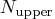$n_{\rm upper}$ , a note is printed in the log file indicating how many subsets exist.

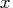
refers to an

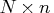matrix

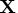of regressors.

Missing values are not permitted in

. Missing values in opt cause the default value to be used.

The MCD subroutine returns the following values:

sc

is a column vector containing the following scalar information:

sc[1]: the quantile 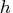used in the objective function
sc[2]: number of subsets generated
sc[3]: number of subsets with singular linear systems
sc[4]: number of nonzero weights
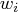
sc[5]: lowest value of the objective function $f_{\rm mcd}$ attained (smallest determinant)
sc[6]: Mahalanobis-like distance used in the computation of the lowest value of the objective function $f_{\rm mcd}$
sc[7]: the cutoff value used for the outlier decision

coef

is a matrix with

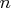columns containing the following results in its rows:

coef[1]: location of ellipsoid center
coef[2]: eigenvalues of final robust scatter matrix
coef[3:2+n]: the final robust scatter matrix for opt[2]=1 or opt[2]=3
coef[2+n+1:2+2n]: the final robust correlation matrix for opt[3]=1 or opt[3]=3

dist

is a matrix with

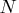columns containing the following results in its rows:

dist[1]: Mahalanobis distances
dist[2]: robust distances based on the final estimates
dist[3]: weights (=1 for small, =0 for large robust distances)

Example

Consider Brownlee's (1965) stackloss data used in the example for the MVE subroutine.

For and (three explanatory variables including intercept), you obtain a total of 5,985 different subsets of 4 observations out of 21. If you decide not to specify optn[5], the MCD algorithm chooses 500 random sample subsets, as in the following code:

  
         /* X1 X2  X3   Y  Stackloss data */ 
     aa = { 1  80  27  89  42, 
            1  80  27  88  37, 
            1  75  25  90  37, 
            1  62  24  87  28, 
            1  62  22  87  18, 
            1  62  23  87  18, 
            1  62  24  93  19, 
            1  62  24  93  20, 
            1  58  23  87  15, 
            1  58  18  80  14, 
            1  58  18  89  14, 
            1  58  17  88  13, 
            1  58  18  82  11, 
            1  58  19  93  12, 
            1  50  18  89   8, 
            1  50  18  86   7, 
            1  50  19  72   8, 
            1  50  19  79   8, 
            1  50  20  80   9, 
            1  56  20  82  15, 
            1  70  20  91  15 };

  
   a = aa[,2:4]; 
   optn = j(8,1,.); 
   optn[1]= 2;              /* ipri */ 
   optn[2]= 1;              /* pcov: print COV */ 
   optn[3]= 1;              /* pcor: print CORR */ 
  
   CALL MCD(sc,xmcd,dist,optn,a);

The first part of the output of this program is a summary of the MCD algorithm and the final points selected, as follows:

  
               Fast MCD by Rousseeuw and Van Driessen 
  
            Number of Variables                            3 
            Number of Observations                        21 
            Default Value for h                           12 
            Specified Value for h                         12 
            Breakdown Value                            42.86 
            - Highest Possible Breakdown Value - 
  
 The best half of the entire data set obtained after full 
 iteration consists of the cases: 
  
  
 4    5    6    7    8    9   10   11   12   13   14   20

The second part of the output is the MCD estimators of the location, scatter matrix, and correlation matrix, as follows:

  
                  MCD Location Estimate 
  
              VAR1              VAR2              VAR3 
  
              59.5      20.833333333      87.333333333 
               Average of 12 Selected Points 
  
                  MCD Scatter Matrix Estimate 
  
                      VAR1              VAR2              VAR3 
  
    VAR1      5.1818181818      4.8181818182      4.7272727273 
    VAR2      4.8181818182      7.6060606061      5.0606060606 
    VAR3      4.7272727273      5.0606060606      19.151515152 
                    Determinant = 238.07387929 
             Covariance Matrix of 12 Selected Points 
  
                      MCD Correlation Matrix 
  
                      VAR1              VAR2              VAR3 
  
    VAR1                 1      0.7674714142      0.4745347313 
    VAR2      0.7674714142                 1      0.4192963398 
    VAR3      0.4745347313      0.4192963398                 1 
  
 The MCD scatter matrix is multiplied by a factor to make it 
 consistent when all the data come from a single Gaussian 
 distribution. 
  
                    Consistent Scatter Matrix 
  
                      VAR1              VAR2              VAR3 
  
    VAR1      8.6578437815      8.0502757968      7.8983838007 
    VAR2      8.0502757968      12.708297013      8.4553211199 
    VAR3      7.8983838007      8.4553211199      31.998580526 
                    Determinant = 397.77668436

The final output presents a table containing the classical Mahalanobis distances, the robust distances, and the weights identifying the outlying observations (that is, leverage points when explaining with these three regressor variables):

  
        Classical Distances and Robust (Rousseeuw) Distances 
                  Unsquared Mahalanobis Distance and 
           Unsquared Rousseeuw Distance of Each Observation 
                 Mahalanobis          Robust 
           N       Distances       Distances          Weight 
  
           1        2.253603       12.173282               0 
           2        2.324745       12.255677               0 
           3        1.593712        9.263990               0 
           4        1.271898        1.401368        1.000000 
           5        0.303357        1.420020        1.000000 
           6        0.772895        1.291188        1.000000 
           7        1.852661        1.460370        1.000000 
           8        1.852661        1.460370        1.000000 
           9        1.360622        2.120590        1.000000 
          10        1.745997        1.809708        1.000000 
          11        1.465702        1.362278        1.000000 
          12        1.841504        1.667437        1.000000 
          13        1.482649        1.416724        1.000000 
          14        1.778785        1.988240        1.000000 
          15        1.690241        5.874858               0 
          16        1.291934        5.606157               0 
          17        2.700016        6.133319               0 
          18        1.503155        5.760432               0 
          19        1.593221        6.156248               0 
          20        0.807054        2.172300        1.000000 
          21        2.176761        7.622769               0 
  
         Robust distances are based on reweighted estimates. 
  
  The cutoff value is the square root of the 0.975 quantile of 
 the chi square distribution with 3 degrees of freedom. 
  
 Points whose robust distance exceeds 3.0575159206 have received 
 a zero weight in the last column above. 
  
                There were 9 such points in the data. 
                  These may include boundary cases. 
   Only points whose robust distance is substantially larger 
 than the cutoff should be considered outliers.

Top of Page