Statistical Computations :: SAS/Genetics(TM) 13.1 User's Guide

Statistical Computations

Subsections:

TDT
S-TDT
SDT
RC-TDT
X-Linked Version of Tests
Permutation Tests

For all tests, it is assumed that the marker has two alleles, $M_1$ and $M_2$ . Extensions to multiallelic markers are made by performing the tests on each allele in turn, with the current allele being considered to be $M_1$ and all other alleles considered to be $M_2$ . When the CONTCORR option is specified in the PROC FAMILY statement, the $z$ score statistics of all versions of the TDT, S-TDT, and RC-TDT can be continuity corrected by subtracting 0.5 from the absolute value of the numerator. The two-sided $p$ -value for each $z$ score using the normal distribution is equivalent to using the $p$ -value from the $\chi ^2_1$ distribution for the square of the $z$ score, and this chi-square form of the statistic is reported in the output data set.

TDT

The TDT (Spielman, McGinnis, and Ewens, 1993) is implemented using a normal approximation. This test includes families where both parents have been genotyped for the marker and at least one is heterozygous. If only one parent has been genotyped, that parent is heterozygous, and the affected child is not homozygous and does not have the same genotype as the typed parent, then the TDT can be applied to this family as well (Curtis and Sham, 1995). The TDT tests for equality between the proportion of times a heterozygous parent transmits the $M_1$ allele to an affected child and the proportion of times a heterozygous parent transmits the $M_2$ allele to an affected child. The normal approximation to the binomial is used to form the $z$ score statistic

$Z = \frac{b- \frac{b+c}{2}}{\sqrt {\frac{b+c}{4}}}$

where $b$ is the number of $M_1$ alleles in affected children from heterozygous parents and $c$ is the number of $M_2$ alleles in affected children from heterozygous parents.

Two extensions to a multiallelic TDT are available. The first, which is performed by default or when MULT=JOINT is specified in the PROC FAMILY statement, combines the TDT for each of $k$ alleles at a marker into one statistic as follows (Spielman and Ewens, 1996):

$T_ J = \frac{k-1}{k} \sum _{v=1}^ k Z^2_ v$

where $Z_ v$ is simply the $Z$ defined in the preceding paragraph, with allele $M_ v$ treated as $M_1$ and all other alleles as $M_2$ for each $v=1,\ldots ,k$ . $T_ J$ and the continuity-corrected form $T’_ J$ have an asymptotic $\chi ^2_{k-1}$ distribution, and the corresponding $p$ -value is reported.

Alternatively, if the MULT=MAX option is specified, either $z_ m$ or $z’_ m$ (when the CONTCORR option is specified) is used, where $z_ m = \max _{1 \le v \le k} |Z_ v|$ . The equivalent one degree of freedom chi-square statistic is reported, and a Bonferroni correction is applied to its $p$ -value.

Note: The TDT is a valid test of linkage and association only when the data consist of unrelated nuclear families and each family contains only one affected child. Otherwise, it is a valid test of linkage only.

S-TDT

The $z$ score procedure given by Spielman and Ewens (1998) is used to calculate $p$ -values for the S-TDT. This test can be applied to families where there are at least one affected sibling and one unaffected sibling, and not all siblings have the same genotype. The $z$ score, whose two-sided $p$ -value is approximated using the normal distribution, is calculated as $z=(Y-A) / \sqrt {V}$ . $Y$ represents the total observed number of $M_1$ alleles in the affected siblings. For $t$ total siblings in the family, $a$ affected and $u$ unaffected, and $r$ that are $M_1/M_1$ and $s$ that are $M_1/M_2$ , summing over families gives

$A=\sum (2r+s)a/t$

and

$V=\sum au[4r(t-r-s)+s(t-s)] / [t^2(t-1)]$

as the expected value and variance of $Y$ , respectively.

When the COMBINE option is specified in the PROC FAMILY statement, the S-TDT and TDT are combined as follows: the TDT is applied to all alleles within a family that meet the requirements described in the preceding section. The S-TDT is then applied to the remaining alleles within a family that meet its requirements described in the preceding paragraph. Using the notation already given for these tests, the $z$ score for the combined test can then be written as

$Z = \frac{(Y + b) - (A + \frac{b+c}{2})}{\sqrt {V + \frac{b+c}{4} }}$

For multiallelic markers, the same extensions can be made to the S-TDT and combined S-TDT that were made to the TDT (Monks, Kaplan, and Weir, 1998); that is, either a joint test over all alleles (using $T_{\mbox{mcomb}}$ ) or the maximum $z$ score of all the alleles with the $p$ -value being Bonferroni-corrected.

Note: The S-TDT is a valid test of linkage and association only when the data consist of unrelated nuclear families and each family contains only one affected and one unaffected sibling. Otherwise, it is a valid test of linkage only.

SDT

The SDT (Horvath and Laird, 1998) is a sign test used on discordant sibling pairs. As with the S-TDT, one affected sibling and one unaffected sibling are required to be in each family, but unlike the S-TDT, the SDT remains a valid test of linkage and association when the sibship is larger.

The notation from the S-TDT is used, except now the quantities $a,u,r,s,$ and $Y$ are defined for each sibship/family, so, for example, there are $a$ affected siblings in the family and $u$ unaffected siblings in the family. Treating each allele $M_ v$ in turn as $M_1$ and all other alleles as $M_2$ , $v=1,\ldots ,k$ , define for each family in the data the average number of $v$ alleles among affected siblings and unaffected siblings respectively as

$m^ a_ v=Y / a$

$m^ u_ v= \left[(2r+s)-Y\right] / u$

Then $d_ v=m_ v^ a-m_ v^ u$ for each family, and summing over families gives $S_ v = \sum \mbox{sgn}(d_ v)$ , where sgn $(d_ v)=1$ for $d_ v > 0$ , 0 for $d_ v=0$ , and $-1$ for $d_ v<0$ . The joint multiallelic SDT statistic (mSDT) is then defined by Czika and Berry (2002) as $T=\mathbf{SW^-S}$ , where $\mathbf{S}=(S_1,\ldots ,S_ k)’$ and $W_{vw}=\sum \mbox{sgn}(d_ v)\mbox{sgn}(d_ w)$ , $v,w=1,\ldots ,k$ , and $\mathbf{W^-}$ is the Moore-Penrose generalized inverse of $\mathbf{W}$ . $T$ has an asymptotic $\chi ^2_{k}$ distribution, where $k’=\mbox{rank}(\mathbf{W})$ , and this distribution is used to obtain $p$ -values for the SDT (Czika and Berry, 2002). When there are only two alleles at the marker, this joint multiallelic version of the SDT reduces to the biallelic version of the SDT.

This sibship test is also combined with the TDT when the COMBINE option in the PROC FAMILY statement is specified, creating a test that can potentially use more of the data (Horvath and Laird, 1998; Curtis, Miller, and Sham, 1999). In order to maintain the test’s validity as a test of association in families with more than one affected and one unaffected sibling, a nonparametric multiallelic TDT is used, which is in the same $\mathbf{SW^-S}$ form as the SDT. This test statistic for the joint test also has an asymptotic $\chi ^2_{k}$ distribution (Czika and Berry, 2002), and the corresponding $p$ -value is reported.

When the MULT=MAX option is specified in the PROC FAMILY statement, then the SDT chi-square statistic is simply $\max _{1\leq v \leq k} (S_ v^2 W^{-1}_{vv})$ and has one degree of freedom. This applies to the SDT when used alone or combined with the TDT. As with the other tests, a Bonferroni correction is made to the $p$ -value.

RC-TDT

The RC-TDT (Knapp, 1999a) takes the combined S-TDT a step further by reconstructing missing parental genotypes when possible in order to use more families. The RC-TDT can be applied to families with at least one affected child that meet one of the following conditions:

Both parents are typed with at least one heterozygous for $M_1$ .
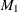One parent is typed, the other can be reconstructed, and at least one parent is heterozygous for $M_1$ .
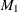Both parents’ genotypes are missing but can be reconstructed, and at least one parent is heterozygous for $M_1$ .
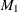At least one parental genotype is missing and cannot be reconstructed, but the conditions for the S-TDT are met.
One parental genotype is missing and cannot be reconstructed, the other parent is heterozygous for 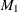$M_1$ , and at least one affected child is heterozygous for 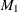$M_1$ and an allele not in the typed parent (Knapp, 1999b).

Reconstruction of parental genotypes is attempted only when there are no genotyping errors in the family for the marker being tested. As with the S-TDT, a $z$ score is created using the statistic $Y$ , but Knapp (1999a) calculates a different expected value $e$ and variance $v$ of $Y$ , which takes into account the bias created by the genotype reconstruction, to form the $z$ score over all families:

$Z = (Y-e)/ \sqrt {v}$

For multiallelic markers, the same extensions can be made to the RC-TDT that were made to the TDT and S-TDT–that is, either a joint test over all alleles, or the maximum $z$ score of all the alleles with the $p$ -value being Bonferroni-corrected.

Note: The RC-TDT is a valid test of linkage and association only when the data consist of unrelated nuclear families and each family contains only one affected and one unaffected sibling. Otherwise, it is a valid test of linkage only.

X-Linked Version of Tests

For markers from the X-chromosome that are specified in the XLVAR statement, the preceding tests are not applicable since females have two alleles at such markers and males have only one. Horvath, Laird, and Knapp (2000) presented X-linked versions of the TDT, S-TDT, combined S-TDT, and RC-TDT that accommodate these markers. For the X-TDT, the only difference in calculating the values $b$ and $c$ is that for X-linked markers, transmissions only from heterozygous mothers, instead of heterozygous parents, are used. Note that even though the paternal genotype is not directly used, it must be nonmissing except for when including transmissions to sons in the family, or for daughters who are heterozygous but with a different genotype than their mother (not possible for a biallelic marker).

For the XS-TDT, each sibship is divided into two subsibships so that female sibs and male sibs are analyzed separately. The statistic is then constructed treating the subsibships independently. For female sibs, the parameters $A$ and $V$ are the same as those defined for the S-TDT. For male sibs, the X-linked expected value and variance of the number of $M_ v$ alleles in affected siblings is calculated across male subsibships as

$A=\sum ac/t$

and

$V=\sum auc(t-c) / [t^2(t-1)]$

where $c$ is the number of $M_ v$ alleles among all males in a subsibship. The X-linked version of the combined S-TDT is calculated analogously to the combined S-TDT for autosomal markers by using the X-linked versions of the TDT and S-TDT.

The X-linked RC-TDT can be divided into four situations:

Both parents are typed and the X-TDT can be applied.
Only the maternal genotype is missing.
Only the paternal genotype is missing.
Both parental genotypes are missing.

(Note that the first situation also includes the preceding exception when the maternal genotype is nonmissing). Horvath, Laird, and Knapp (2000) show, as with the original RC-TDT, expected values and variances of the number of $M_1$ alleles in affected children when reconstructing parental genotypes in each of the last three situations listed. Using these values, the XRC-TDT can be formed identically to the statistic for the RC-TDT shown in the preceding section.

Permutation Tests

By default, $p$ -values from the asymptotic $\chi ^2$ distribution with appropriate degrees of freedom are reported for all tests. However, if the PERMS= option is specified in the PROC FAMILY statement, then Monte Carlo estimates of exact $p$ -values are calculated using the permutation procedure for the TDT, S-TDT, SDT, and combined S-TDT and SDT. When the TDT is being performed, including when it is performed in the combined tests, new samples are formed by permuting the alleles that are transmitted to the offspring from the parents and those that are not transmitted (Kaplan, Martin, and Weir, 1997). Each affected child in a nuclear family is assigned a genotype comprising one allele from each parent, with each allele being randomly selected from the pair possessed by an individual parent. When the sibling tests are used and the parental information is ignored, the permutation procedure involves randomly permuting the affection status of siblings within each sibship (Spielman and Ewens, 1998; Monks, Kaplan, and Weir, 1998). For each test, the corresponding test statistic is calculated for the original sample as well as each of the permuted samples. The approximation to the exact $p$ -value is then calculated as the number of times the test statistic from a permuted sample exceeds the test statistic from the original sample.

The FAMILY Procedure