The ALLELE Procedure
The genetic structure of populations can be characterized by Wright’s ![]() statistics (1951) measuring the degree of relatedness between different types of allele pairs. Cockerham (1969, 1973) defines these same quantities in an analysis-of-variance (ANOVA) framework. For a population hierarchy defined by the variable
in the POP statement, these measures include
statistics (1951) measuring the degree of relatedness between different types of allele pairs. Cockerham (1969, 1973) defines these same quantities in an analysis-of-variance (ANOVA) framework. For a population hierarchy defined by the variable
in the POP statement, these measures include ![]() and, when HWE is not assumed,
and, when HWE is not assumed, ![]() and
and ![]() , corresponding to Wright’s
, corresponding to Wright’s ![]() ,
, ![]() , and
, and ![]() , respectively. A weighted average of these measures over loci can be reported as an overall measure, and measures for individual
loci can be requested as well. The estimates of these parameters are calculated using an ANOVA structure along with a method-of-moments
approach.
, respectively. A weighted average of these measures over loci can be reported as an overall measure, and measures for individual
loci can be requested as well. The estimates of these parameters are calculated using an ANOVA structure along with a method-of-moments
approach.
For genotypic data with unknown phase from ![]() populations, variation can be partitioned into three sources: between populations, between individuals within populations,
and within individuals, with respective observed mean squares
populations, variation can be partitioned into three sources: between populations, between individuals within populations,
and within individuals, with respective observed mean squares ![]() ,
, ![]() , and
, and ![]() . Using the method of moments to equate estimates of the variance components with functions of the observed mean squares,
the coancestry coefficients can be estimated as follows:
. Using the method of moments to equate estimates of the variance components with functions of the observed mean squares,
the coancestry coefficients can be estimated as follows:
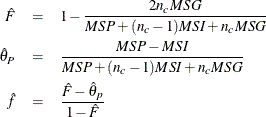
where ![]() for
for ![]() populations.
populations.
If HWE is assumed in a two-level population hierarchy, the data can be treated as haploid data where allele, not genotype,
frequencies are used in the calculations. Also, in this scenario, ![]() and
and ![]() are equal and
are equal and ![]() . Thus, there is only one parameter to estimate,
. Thus, there is only one parameter to estimate, ![]() , which represents the covariance of alleles from the same population relative to the covariance between alleles from different
populations, estimated as follows:
, which represents the covariance of alleles from the same population relative to the covariance between alleles from different
populations, estimated as follows:
where the counts used in ![]() are now in terms of alleles instead of individuals.
are now in terms of alleles instead of individuals.
Tests of hypotheses that these parameters are 0 can be executed via permutation tests. A different permutation scheme is used for each parameter under each population structure scenario. The schemes displayed in Table 2.2 “Permutation Schemes for Population Structure Parameters” are derived from Excoffier and Lischer (2011).
Table 2.2: Permutation Schemes for Population Structure Parameters
|
Parameter |
|
Permutation Scheme |
|---|---|---|
|
|
Yes |
Individuals among populations |
|
|
No |
Individuals among populations |
|
|
No |
Alleles among populations |
|
|
No |
Alleles within populations |
