Example 10.1 Monoecious Population Analysis
The following example shows a covariance analysis within nonoverlapping generations for a monoecious population. Parents of generation 1 are unknown and therefore assumed to be unrelated. The following statements produce Output 10.1.1 through Output 10.1.3:
data Monoecious;
input Generation Individual Parent1 Parent2 Covariance @@;
datalines;
1 1 . . . 1 2 . . . 1 3 . . .
2 1 1 1 . 2 2 1 2 . 2 3 2 3 .
3 1 1 2 . 3 2 1 3 . 3 3 2 1 .
3 4 1 3 . 3 . 2 3 0.50 3 . 4 3 1.135
;
title 'Inbreeding within Nonoverlapping Generations';
proc inbreed ind covar matrix data=Monoecious;
class Generation;
run;
Output 10.1.1
Monoecious Population Analysis, Generation 1
The INBREED Procedure
Generation = 1
| 1.0000 |
. |
. |
| . |
1.0000 |
. |
| . |
. |
1.0000 |
Output 10.1.2
Monoecious Population Analysis, Generation 2
The INBREED Procedure
Generation = 2
| 1.5000 |
0.5000 |
. |
| 0.5000 |
1.0000 |
0.2500 |
| . |
0.2500 |
1.0000 |
Output 10.1.3
Monoecious Population Analysis, Generation 3
The INBREED Procedure
Generation = 3
| 1.2500 |
0.5625 |
0.8750 |
0.5625 |
| 0.5625 |
1.0000 |
1.1349 |
0.6250 |
| 0.8750 |
1.1349 |
1.2500 |
1.1349 |
| 0.5625 |
0.6250 |
1.1349 |
1.0000 |
| 1.2500 |
| 1.0000 |
| 1.2500 |
| 1.0000 |
Note that, since the parents of the first generation are unknown, off-diagonal elements of the covariance matrix are all 0s and on-diagonal elements are all 1s. If there is an INIT=cov value, then the off-diagonal elements would be equal to cov, while on-diagonal elements would be equal to 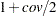 .
.
In the third generation, individuals 2 and 4 are full siblings, so they belong to the same family. Since PROC INBREED computes covariance coefficients between families, the second and fourth columns of inbreeding coefficients are the same, except that their intersections with the second and fourth rows are reordered. Notice that, even though there is an observation to assign a covariance of 0.50 between individuals 2 and 3 in the third generation, the covariance between 2 and 3 is set to 1.135, the same value assigned between 4 and 3. This is because families get the same covariances, and later specifications override previous ones.
Copyright © SAS Institute Inc. All rights reserved.
 .
. 