The ALLELE Procedure
Testing for Hardy-Weinberg Equilibrium
Under ideal population conditions, the two alleles an individual receives, one from each parent, are independent so that 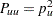 and
and 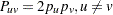 . The factor of 2 for heterozygotes recognizes the fact that
. The factor of 2 for heterozygotes recognizes the fact that 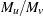 and
and 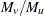 genotypes are generally indistinguishable. This statement about allelic independence within loci is called Hardy-Weinberg equilibrium (HWE). Forces such as selection, mutation, and migration in a population or nonrandom mating can cause departures from HWE. Two methods are used here for testing a marker for HWE, both of which can accommodate any number of alleles. Both methods are testing the hypothesis that
genotypes are generally indistinguishable. This statement about allelic independence within loci is called Hardy-Weinberg equilibrium (HWE). Forces such as selection, mutation, and migration in a population or nonrandom mating can cause departures from HWE. Two methods are used here for testing a marker for HWE, both of which can accommodate any number of alleles. Both methods are testing the hypothesis that 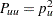 and
and 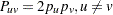 for all
for all 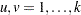 .
.
Chi-Square Goodness-of-Fit Test
The chi-square goodness-of-fit test can be used to test markers for HWE. The chi-square statistic
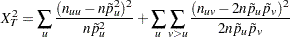 |
has 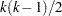 degrees of freedom (df), where
degrees of freedom (df), where 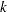 is the number of alleles at the marker locus.
is the number of alleles at the marker locus.
Permutation Version of Exact Test
The permutation version of the exact test given by Guo and Thompson (1992) is based on the conditional probability of genotype counts given allelic counts and the hypothesis of allelic independence. The probability of the observed genotype counts under this hypothesis is
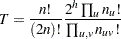 |
where 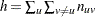 is the number of heterozygous individuals. Significance levels are calculated by the Monte Carlo permutation procedure. The
is the number of heterozygous individuals. Significance levels are calculated by the Monte Carlo permutation procedure. The 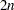 alleles are randomly permuted the number of times indicated in the PERMS=
option to form new sets of
alleles are randomly permuted the number of times indicated in the PERMS=
option to form new sets of  genotypes. The significance level is then calculated as the proportion of times the value of
genotypes. The significance level is then calculated as the proportion of times the value of 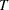 for each set of permuted data does not exceed the value of
for each set of permuted data does not exceed the value of 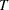 for the actual data. You can indicate the random seed used to randomly permute the data in the SEED=
option of the PROC ALLELE statement.
for the actual data. You can indicate the random seed used to randomly permute the data in the SEED=
option of the PROC ALLELE statement.
