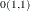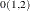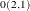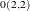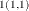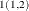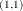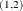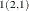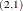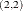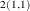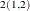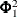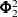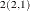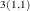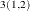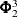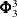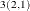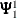The STATESPACE Procedure

OUTAR= Data Set

The OUTAR= data set contains the estimates of the preliminary autoregressive models. The OUTAR= data set contains the following variables:

ORDER, a numeric variable that contains the order p of the autoregressive model that the observation represents
AIC, a numeric variable that contains the value of the information criterion ${AIC_{p}}$
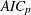
SIGFl, numeric variables that contain the estimate of the innovation covariance matrices for the forward autoregressive models. The variable SIGFl contains the lth column of 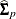${\widehat{\bSigma }_{p}}$ in the observations with ORDER=p.
SIGBl, numeric variables that contain the estimate of the innovation covariance matrices for the backward autoregressive models. The variable SIGBl contains the lth column of 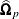${\widehat{\bOmega }_{p}}$ in the observations with ORDER=p.
FORk _l, numeric variables that contain the estimates of the autoregressive parameter matrices for the forward models. The variable FORk _l contains the lth column of the lag k autoregressive parameter matrix 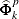${ \widehat{\bPhi }^{p}_{k}}$ in the observations with ORDER=p.
BACk _l, numeric variables that contain the estimates of the autoregressive parameter matrices for the backward models. The variable BACk _l contains the lth column of the lag k autoregressive parameter matrix 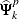${ \widehat{\bPsi }^{p}_{k}}$ in the observations with ORDER=p.

The estimates for the order p autoregressive model can be selected as those observations with ORDER=p. Within these observations, the k,lth element of 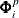${ \bPhi ^{p}_{i}}$ is given by the value of the FORi _l variable in the kth observation. The k,lth element of 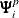${ \bPsi ^{p}_{i}}$ is given by the value of BACi _l variable in the kth observation. The k,lth element of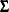 $\bSigma$ $_{\mi{p} }$ is given by SIGFl in the kth observation. 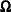The k,lth element of $\bOmega$ $_{\mi{p}}$ is given by SIGBl in the kth observation.

Table 35.2 shows an example of the OUTAR= data set, with ARMAX=3 and 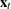${\mb{x}_{t}}$ of dimension 2. In Table 35.2, 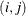${(i,j)}$ indicate (i, (n) element of the matrix.

Table 35.2: Values in the OUTAR= Data Set

Obs	ORDER	AIC	SIGF1	SIGF2	SIGB1	SIGB2	FOR1_1	FOR1_2	FOR2_1	FOR2_2	FOR3_1
1	0	AIC $_{0}$	$\bSigma$ $_{0(1,1)}$	$\bSigma$ $_{0(1,2)}$	$\bOmega$ $_{0(1,1)}$	$\bOmega$ $_{0(1,2)}$	.	.	.	.	.
2	0	AIC $_{0}$	$\bSigma$ $_{0(2,1)}$	$\bSigma$ $_{0(2,2)}$	$\bOmega$ $_{0(2,1)}$	$\bOmega$ $_{0(2,2)}$	.	.	.	.	.
3	1	AIC $_{1}$	$\bSigma$ $_{1(1,1)}$	$\bSigma$ $_{1(1,2)}$	$\bOmega$ $_{1(1,1)}$	$\bOmega$ $_{1(1,2)}$	$\bPhi ^{1}_{1}$ $_{(1,1)}$	$\bPhi ^{1}_{1}$ $_{(1,2)}$	.	.	.
4	1	AIC $_{1}$	$\bSigma$ $_{1(2,1)}$	$\bSigma$ $_{1(1,2)}$	$\bOmega$ $_{1(2,1)}$	$\bOmega$ $_{1(1,2)}$	$\bPhi ^{1}_{1}$ $_{(2,1)}$	$\bPhi ^{1}_{1}$ $_{(2,2)}$	.	.	.
5	2	AIC $_{2}$	$\bSigma$ $_{2(1,1)}$	$\bSigma$ $_{2(1,2)}$	$\bOmega$ $_{2(1,1)}$	$\bOmega$ $_{2(1,2)}$	$\bPhi ^{2}_{1}$ $_{(1,1)}$	$\bPhi ^{2}_{1}$ $_{(1,2)}$	$\bPhi ^{2}_{2}$ $_{(1,1)}$	$\bPhi ^{2}_{2}$ $_{(1,2)}$	.
6	2	AIC $_{2}$	$\bSigma$ $_{2(2,1)}$	$\bSigma$ $_{2(1,2)}$	$\bOmega$ $_{2(2,1)}$	$\bOmega$ $_{2(1,2)}$	$\bPhi ^{2}_{1}$ $_{(2,1)}$	$\bPhi ^{2}_{1}$ $_{(2,2)}$	$\bPhi ^{2}_{2}$ $_{(2,1)}$	$\bPhi ^{2}_{2}$ $_{(2,2)}$	.
7	3	AIC $_{3}$	$\bSigma$ $_{3(1,1)}$	$\bSigma$ $_{3(1,2)}$	$\bOmega$ $_{3(1,1)}$	$\bOmega$ $_{3(1,2)}$	$\bPhi ^{3}_{1}$ $_{(1,1)}$	$\bPhi ^{3}_{1}$ $_{(1,2)}$	$\bPhi ^{3}_{2}$ $_{(1,1)}$	$\bPhi ^{3}_{2}$ $_{(1,2)}$	$\bPhi ^{3}_{3}$ $_{(1,1)}$
8	3	AIC $_{3}$	$\bSigma$ $_{3(2,1)}$	$\bSigma$ $_{3(1,2)}$	$\bOmega$ $_{3(2,1)}$	$\bOmega$ $_{3(1,2)}$	$\bPhi ^{3}_{1}$ $_{(2,1)}$	$\bPhi ^{3}_{1}$ $_{(2,2)}$	$\bPhi ^{3}_{2}$ $_{(2,1)}$	$\bPhi ^{3}_{2}$ $_{(2,2)}$	$\bPhi ^{3}_{3}$ $_{(2,1)}$

Obs	FOR3_2	BACK1_1	BACK1_2	BACK2_1	BACK2_2	BACK3_1	BACK3_2
1	.	.	.	.	.	.	.
2	.	.	.	.	.	.	.
3	.	$\bPsi ^{1}_{1}$ $_{(1,1)}$	$\bPsi ^{1}_{1}$ $_{(1,2)}$	.	.	.	.
4	.	$\bPsi ^{1}_{1}$ $_{(2,1)}$	$\bPsi ^{1}_{1}$ $_{(2,2)}$	.	.	.	.
5	.	$\bPsi ^{2}_{1}$ $_{(1,1)}$	$\bPsi ^{2}_{1}$ $_{(1,2)}$	$\bPsi ^{2}_{2}$ $_{(1,1)}$	$\bPsi ^{2}_{2}$ $_{(1,2)}$	.	.
6	.	$\bPsi ^{2}_{1}$ $_{(2,1)}$	$\bPsi ^{2}_{1}$ $_{(2,2)}$	$\bPsi ^{2}_{2}$ $_{(2,1)}$	$\bPsi ^{2}_{2}$ $_{(2,2)}$	.	.
7	$\bPhi ^{3}_{3}$ $_{(1,2)}$	$\bPsi ^{3}_{1}$ $_{(1,1)}$	$\bPsi ^{3}_{1}$ $_{(1,2)}$	$\bPsi ^{3}_{2}$ $_{(1,1)}$	$\bPsi ^{3}_{2}$ $_{(1,2)}$	$\bPsi ^{3}_{3}$ $_{(1,1)}$	$\bPsi ^{3}_{3}$ $_{(1,2)}$
8	$\bPhi ^{3}_{3}$ $_{(2,2)}$	$\bPsi ^{3}_{1}$ $_{(2,1)}$	$\bPsi ^{3}_{1}$ $_{(2,2)}$	$\bPsi ^{3}_{2}$ $_{(2,1)}$	$\bPsi ^{3}_{2}$ $_{(2,2)}$	$\bPsi ^{3}_{3}$ $_{(2,1)}$	$\bPsi ^{3}_{3}$ $_{(2,2)}$

The estimated autoregressive parameters can be used in the IML procedure to obtain autoregressive estimates of the spectral density function or forecasts based on the autoregressive models.