The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples
 Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects
Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects - References
Example 30.8 Predicting Mean and Value-at-Risk by Using Scoring Functions
If you work in the risk management department of an insurance company or a bank, then one of your primary applications of
severity loss distribution models is to predict the value-at-risk (VaR) so that there is a very low probability of experiencing
a loss value that is greater than the VaR. The probability level at which VaR is measured is prescribed by industry regulations
such as Basel III and Solvency II. The VaR level is usually specified in terms of 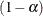 , where
, where 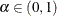 is the probability that a loss value exceeds the VaR. Typical VaR levels are 0.95, 0.975, and 0.995.
is the probability that a loss value exceeds the VaR. Typical VaR levels are 0.95, 0.975, and 0.995.
In addition to predicting the VaR, which is regarded as an estimate of the worst-case loss, businesses are often interested in predicting the average loss by estimating either the mean or median of the distribution.
The estimation of the mean and VaR combined with the scale regression model is very potent tool for analyzing worst-case and average losses for various scenarios. For example, if the regressors that are used in a scale regression model represent some key macroeconomic and operational indicators, which are widely referred to as key risk indicators (KRIs), then you can analyze the VaR and mean loss estimates over various values for the KRIs to get a more comprehensive picture of the risk profile of your organization across various market and internal conditions.
This example illustrates the use of scoring functions to simplify the process of predicting the mean and VaR of scale regression models.
To compute the mean, you need to ensure that the function to compute the mean of a distribution is available in the function
library. If you define and fit your own distribution and you want to compute its mean, then you need to use the FCMP procedure
to define that function and you need to use the CMPLIB= system option to specify the location of that function. For your convenience,
the dist_MEAN function (which computes the mean of the dist distribution) is already defined in the Sashelp.Svrtdist library for each of the 10 predefined distributions. The following statements display the definitions of MEAN functions of
all distributions. Note that the MEAN functions for the Burr, Pareto, and generalized Pareto distributions check the existence
of the first moment for specified parameter values.
/*--------- Define distribution functions that compute the mean ----------*/
proc fcmp library=sashelp.svrtdist outlib=work.means.scalemod;
function BURR_MEAN(x, Theta, Alpha, Gamma);
if not(Alpha * Gamma > 1) then
return (.); /* first moment does not exist */
return (Theta*gamma(1 + 1/Gamma)*gamma(Alpha - 1/Gamma)/gamma(Alpha));
endsub;
function EXP_MEAN(x, Theta);
return (Theta);
endsub;
function GAMMA_MEAN(x, Theta, Alpha);
return (Theta*Alpha);
endsub;
function GPD_MEAN(x, Theta, Xi);
if not(Xi < 1) then
return (.); /* first moment does not exist */
return (Theta/(1 - Xi));
endsub;
function IGAUSS_MEAN(x, Theta, Alpha);
return (Theta);
endsub;
function LOGN_MEAN(x, Mu, Sigma);
return (exp(Mu + Sigma*Sigma/2.0));
endsub;
function PARETO_MEAN(x, Theta, Alpha);
if not(Alpha > 1) then
return (.); /* first moment does not exist */
return (Theta/(Alpha - 1));
endsub;
function STWEEDIE_MEAN(x, Theta, Lambda, P);
return (Theta* Lambda * (2 - P) / (P - 1));
endsub;
function TWEEDIE_MEAN(x, P, Mu, Phi);
return (Mu);
endsub;
function WEIBULL_MEAN(x, Theta, Tau);
return (Theta*gamma(1 + 1/Tau));
endsub;
quit;
For your further convenience, the dist_QUANTILE function (which computes the quantile of the dist distribution) is also defined in the Sashelp.Svrtdist library for each of the 10 predefined distributions. Because the MEAN and QUANTILE functions satisfy the definition of a
distribution function as described in the section Formal Description, you can submit the following PROC SEVERITY step to fit all regression-friendly predefined distributions and generate the
scoring functions for the MEAN, QUANTILE, and other distribution functions:
/*----- Fit all distributions and generate scoring functions ------*/ proc severity data=test_sev8 outest=est print=all plots=none; loss y; scalemodel x1-x5; dist _predefined_ stweedie; outscorelib outlib=scorefuncs commonpackage; run;
The SAS statements that simulate the sample in the Work.Test_sev8 data set are available in the PROC SEVERITY sample program sevex08.sas. The OUTLIB= option in the OUTSCORELIB statement requests that the scoring functions be written to the Work.Scorefuncs library, and the COMMONPACKAGE option in the OUTSCORELIB statement requests that all the functions be written to the same
package. Upon completion, PROC SEVERITY sets the CMPLIB system option to the following value:
(sashelp.svrtdist work.scorefuncs)
The "All Fit Statistics" table in Output 30.8.1 shows that the lognormal distribution’s scale model is the best and the inverse Gaussian’s scale model is a close second according to the likelihood-based statistics.
Output 30.8.1: Comparison of Fitted Scale Models for Mean and VaR Illustration
| All Fit Statistics | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | -2 Log Likelihood |
AIC | AICC | BIC | KS | AD | CvM | |||||||
| stweedie | 460.65755 | 476.65755 | 476.95083 | 510.37441 | 10.44548 | 64571 | 37.07705 | |||||||
| Burr | 451.42238 | 467.42238 | 467.71565 | 501.13924 | 10.32782 | 42254 | 37.19808 | |||||||
| Exp | 1515 | 1527 | 1527 | 1552 | 8.85827 | 29917 | 23.98267 | |||||||
| Gamma | 448.28222 | 462.28222 | 462.50986 | 491.78448 | 10.42272 | 63712 | 37.19450 | |||||||
| Igauss | 444.44512 | 458.44512 | 458.67276 | 487.94738 | 10.33028 | 83195 | 37.30880 | |||||||
| Logn | 444.43670 | * | 458.43670 | * | 458.66434 | * | 487.93895 | * | 10.37035 | 68631 | 37.18553 | |||
| Pareto | 1515 | 1529 | 1529 | 1559 | 8.85775 | * | 29916 | * | 23.98149 | * | ||||
| Gpd | 1515 | 1529 | 1529 | 1559 | 8.85827 | 29917 | 23.98267 | |||||||
| Weibull | 527.28676 | 541.28676 | 541.51440 | 570.78902 | 10.48084 | 72814 | 36.36039 | |||||||
| Note: The asterisk (*) marks the best model according to each column's criterion. | ||||||||||||||
You can examine the scoring functions that are written to the Work.Scorefuncs library by using the FCMP Function Editor, which is available in the Display Manager session of Base SAS when you select
Solutions Analysis from the main menu. For example, PROC SEVERITY automatically generates and submits the following PROC FCMP statements to
define the scoring functions SEV_MEAN_LOGN and SEV_QUANTILE_IGAUSS:
Analysis from the main menu. For example, PROC SEVERITY automatically generates and submits the following PROC FCMP statements to
define the scoring functions SEV_MEAN_LOGN and SEV_QUANTILE_IGAUSS:
proc fcmp library=(sashelp.svrtdist) outlib=work.scorefuncs.sevfit;
function SEV_MEAN_LOGN(y, x{*});
_logscale_=0;
_logscale_ = _logscale_ + ( 7.64722278930350E-01 * x{1});
_logscale_ = _logscale_ + ( 2.99209540369860E+00 * x{2});
_logscale_ = _logscale_ + (-1.00788916253430E+00 * x{3});
_logscale_ = _logscale_ + ( 2.58883602184890E-01 * x{4});
_logscale_ = _logscale_ + ( 5.00927479793970E+00 * x{5});
_logscale_ = _logscale_ + ( 9.95078833050690E-01);
return (LOGN_MEAN(y, _logscale_, 2.31592981635590E-01));
endsub;
function SEV_QUANTILE_IGAUSS(y, x{*});
_logscale_=0;
_logscale_ = _logscale_ + ( 7.64581738373520E-01 * x{1});
_logscale_ = _logscale_ + ( 2.99159055015310E+00 * x{2});
_logscale_ = _logscale_ + (-1.00793496641510E+00 * x{3});
_logscale_ = _logscale_ + ( 2.58870460543840E-01 * x{4});
_logscale_ = _logscale_ + ( 5.00996884646730E+00 * x{5});
_scale_ = 2.77854870591020E+00 * exp(_logscale_);
return (IGAUSS_QUANTILE(y, _scale_, 1.81511227238720E+01));
endsub;
quit;
PROC SEVERITY detects all the distribution functions that are available in the current CMPLIB= search path (which always includes
the Sashelp.Svrtdist library) for the distributions that you specify in the DIST statement, and it creates the corresponding scoring functions.
You can define any distribution function that has the desired signature to compute an estimate of your choice, include its
library in the CMPLIB= system option, and then specify the OUTSCORELIB statement to generate the corresponding scoring functions.
Specifying the COMMONPACKAGE option in the OUTSCORELIB statement causes the name of the scoring function to take the form
SEV_function-suffix_dist. If you do not specify the COMMONPACKAGE option, PROC SEVERITY creates a scoring function named SEV_function-suffix in a package named dist. You can invoke functions from a specific package only inside the FCMP procedure. If you want to invoke the scoring functions
from a DATA step, then it is recommended that you specify the COMMONPACKAGE option when you specify multiple distributions
in the DIST statement.
To illustrate the use of scoring functions, let Work.Reginput contain the scoring data, where the values of regressors in each observation define one scenario. Scoring functions make
it very easy to compute the mean and VaR of each distribution’s scale model for each of the scenarios, as the following steps
illustrate for the lognormal and inverse Gaussian distributions:
/*--- Set VaR level ---*/
%let varLevel=0.975;
/*--- Compute scores (mean and var) for the ---
--- scoring data by using the scoring functions ---*/
data scores;
array x{*} x1-x5;
set reginput;
igauss_mean = sev_mean_igauss(., x);
igauss_var = sev_quantile_igauss(&varLevel, x);
logn_mean = sev_mean_logn(., x);
logn_var = sev_quantile_logn(&varLevel, x);
run;
The preceding steps use a VaR level of 97.5%.
The following DATA step accomplishes the same task by reading the parameter estimates that were written to the Work.Est data set by the previous PROC SEVERITY step:
/*--- Compute scores (mean and var) for the ---
--- scoring data by using the OUTEST= data set ---*/
data scoresWithOutest(keep=x1-x5 igauss_mean igauss_var logn_mean logn_var);
array _x_{*} x1-x5;
array _xparmIgauss_{5} _temporary_;
array _xparmLogn_{5} _temporary_;
retain _Theta0_ Alpha0;
retain _Mu0_ Sigma0;
*--- read parameter estimates for igauss and logn models ---*;
if (_n_ = 1) then do;
set est(where=(upcase(_MODEL_)='IGAUSS' and _TYPE_='EST'));
_Theta0_ = Theta; Alpha0 = Alpha;
do _i_=1 to dim(_x_);
if (_x_(_i_) = .R) then _xparmIgauss_(_i_) = 0;
else _xparmIgauss_(_i_) = _x_(_i_);
end;
set est(where=(upcase(_MODEL_)='LOGN' and _TYPE_='EST'));
_Mu0_ = Mu; Sigma0 = Sigma;
do _i_=1 to dim(_x_);
if (_x_(_i_) = .R) then _xparmLogn_(_i_) = 0;
else _xparmLogn_(_i_) = _x_(_i_);
end;
end;
set reginput;
*--- predict mean and VaR for inverse Gaussian ---*;
* first compute X'*beta for inverse Gaussian *;
_xbeta_ = 0.0;
do _i_ = 1 to dim(_x_);
_xbeta_ = _xbeta_ + _xparmIgauss_(_i_) * _x_(_i_);
end;
* now compute scale for inverse Gaussian *;
_SCALE_ = _Theta0_ * exp(_xbeta_);
igauss_mean = igauss_mean(., _SCALE_, Alpha0);
igauss_var = igauss_quantile(&varLevel, _SCALE_, Alpha0);
*--- predict mean and VaR for lognormal ---*;
* first compute X'*beta for lognormal*;
_xbeta_ = 0.0;
do _i_ = 1 to dim(_x_);
_xbeta_ = _xbeta_ + _xparmLogn_(_i_) * _x_(_i_);
end;
* now compute Mu=log(scale) for lognormal *;
_MU_ = _Mu0_ + _xbeta_;
logn_mean = logn_mean(., _MU_, Sigma0);
logn_var = logn_quantile(&varLevel, _MU_, Sigma0);
run;
The "Values Comparison Summary" table in Output 30.8.2 shows that the difference between the estimates that are produced by both methods is within the acceptable machine precision. However, the comparison of the DATA step complexity of each method clearly shows that the method that uses the scoring functions is much easier because it saves a lot of programming effort. Further, new distribution functions, such as the dist_MEAN functions that are illustrated here, are automatically discovered and converted to scoring functions by PROC SEVERITY. That enables you to focus your efforts on writing the distribution function that computes your desired score, which needs to be done only once. Then, you can create and use the corresponding scoring functions multiple times with much less effort.
Output 30.8.2: Comparison of Mean and VaR Estimates of Two Scoring Methods
Observation Summary
Observation Base Compare
First Obs 1 1
Last Obs 10 10
Number of Observations in Common: 10.
Total Number of Observations Read from WORK.SCORESWITHOUTEST: 10.
Total Number of Observations Read from WORK.SCORES: 10.
Number of Observations with Some Compared Variables Unequal: 0.
Number of Observations with All Compared Variables Equal: 10.
Values Comparison Summary
Number of Variables Compared with All Observations Equal: 9.
Number of Variables Compared with Some Observations Unequal: 0.
Total Number of Values which Compare Unequal: 0.
Total Number of Values not EXACTLY Equal: 40.
Maximum Difference Criterion Value: 2.0963E-13.
|