The PDLREG Procedure

Getting Started: PDLREG Procedure

Subsections:

Introductory Example

Use the MODEL statement to specify the regression model. The PDLREG procedure’s MODEL statement is written like MODEL statements in other SAS regression procedures, except that a regressor can be followed by a lag distribution specification enclosed in parentheses.

For example, the following MODEL statement regresses Y on X and Z and specifies a distributed lag for X:

   model y = x(4,2) z;

The notation X(4,2) specifies that the model includes X and 4 lags of X, with the coefficients of X and its lags constrained to follow a second-degree (quadratic) polynomial. Thus, the regression model specified by this MODEL statement is

$y_{t} = a + b_{0}x_{t} + b_{1}x_{t-1} + b_{2}x_{t-2} + b_{3}x_{t-3} + b_{4}x_{t-4} + c z_{t} + u_{t}$

$b_{i} = {\alpha }_{0} + {\alpha }_{1}f_{1}(i) + {\alpha }_{2}f_{2}(i)$

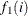where ${f_{1}(i)}$ is a polynomial of degree 1 in i and 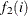${f_{2}(i)}$ is a polynomial of degree 2 in i.

Lag distribution specifications are enclosed in parentheses and follow the name of the regressor variable. The general form of the lag distribution specification is

regressor-name ( length, degree, minimum-degree, end-constraint )

where

length: is the length of the lag distribution—that is, the number of lags of the regressor to use.
degree: is the degree of the distribution polynomial.
minimum-degree: is an optional minimum degree for the distribution polynomial.
end-constraint: is an optional endpoint restriction specification, which can have the value FIRST, LAST, or BOTH.

If the minimum-degree option is specified, the PDLREG procedure estimates models for all degrees between minimum-degree and degree.